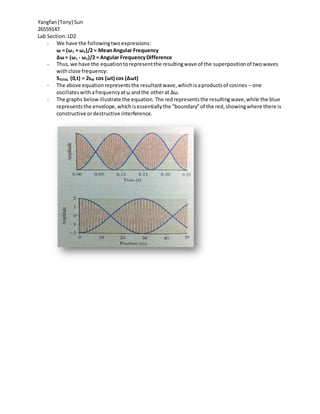
The document discusses various topics relating to interference of waves including constructive and destructive interference, beats, and provides examples of problems relating to these topics. It explains the conditions needed for constructive and destructive interference and how beats occur due to two waves with slightly different frequencies combining to produce a sound that varies in amplitude over time. Several example problems are worked through applying the concepts of interference and beats.

1. Yangfan(Tony) Sun
26559147
Lab Section:LD2
Physics 101 Learning Object 7
Interference of Waves and Beats
Interferenceof 3-DimensionalWaves
Constructive Interference
- For wavesin1-Dimensionthathave equal wavelengthandfrequency,theyhave a“phase
difference”thatisgovernedbydifference of the phase constantsof the twowaves
- Phase differencesare independentof time in1-Dimension butare dependentof time whenthey
traverse indifferentdirectionsratherthanina straightline
- Considertwowaveswithequal wavelengthand frequencyandare inphase
At the pointwhere there isthe highestamplitude forbothwaves,we have the followingfor
constructive interference:
- d1 = mλ, where misa positive integer
d2= nλ, where nisa positive integer
∆d = d2 - d1 = (n– m)λ= pλ,where p is0, ±1, ±2, ±3, …
- From the above conditions,we canconclude that fora constructive interference tooccur, both
paths must each be integermultiplesofthe wavelength

2. Yangfan(Tony) Sun
26559147
Lab Section:LD2
Destructive Interference
- For destructive interference tooccur fortwo wavestravellingindifferentdirections,one wave
mustbe at a large positive amplitude andthe othermustbe at a large negative amplitude so
that the wavesare out of phase and cancel each other
- The conditionfordestructive interference tooccur isas follows:
∆d = d2 - d1 = ((2n+ 1)/2) λ = (n + 1/2)λ, where nis 0, ±1, ±2, ±3, …
- From the above conditions,we canconclude that fora destructive interference tooccur, one
path must be an integernumber of wavelengthswhile the otheris a halfintegermultiple
Beats
What exactlyisa beat?
- A beat is a type of variation in amplitude whentwo waves have slightlydifferentfrequencies,
producinga soundwhere the amplitudeincreasesand decreasesovertime.
- The rate at whichthe amplitude variesisproportional tothe frequencydifference,onlyif itis
small.If the frequencydifference islarge, thenwe heartwoseparate tonesinsteadof one that
changesinintensity.
- You can imagine asituationtomake the above note make sense.Imagine listeningtoa high
pitchsoundand lowpitchsound. You can easilydistinguishthatthere are twodifferenttones.
However,if twosounds are close toeach intermsof frequency,itcanbe quite difficulttotell
the difference,andwhatresultsisusuallyone tone.
- The belowgraphillustrateshowbeatswork.The blue andredsine graphsare two waveswith
differentfrequencies.Asaresult,whichisshownbythe greenwave,we heara soundwiththe
amplitude increasinganddecreasing,andwhenthere isnosoundatall.

3. Yangfan(Tony) Sun
26559147
Lab Section:LD2
- Real life application:If youhave everflownin apassengerplane,youmayhave encountereda
deep,oscillatingengine sound thatbecomesquietthenloudthenquietandso on.Thisis
because there isa beatbetweenthe twoenginesonthe side of the aircraft that have unequal
frequencies.
Image from:
http://www.southampton.ac.uk/engineering/research
/projects/prediction_of_aircraft_exhaust_noise.page
Image from:
http://adg.stanford.edu/aa2
41/noise/noise.html

4. Yangfan(Tony) Sun
26559147
Lab Section:LD2
- We have the followingtwoexpressions:
ω = (ω1 + ω2)/2 = MeanAngular Frequency
∆ω= (ω1 - ω2)/2 = Angular FrequencyDifference
- Thus,we have the equationtorepresentthe resultingwave of the superpositionof twowaves
withclose frequency:
STOTAL (0,t) = 2sM cos (ωt) cos (∆ωt)
- The above equationrepresentsthe resultantwave,whichisaproductsof cosines – one
oscillateswithafrequencyatω andthe otherat ∆ω.
- The graphs below illustrate the equation.The redrepresentsthe resultingwave,while the blue
representsthe envelope,whichisessentiallythe “boundary”of the red,showingwhere there is
constructive ordestructive interference.

5. Yangfan(Tony) Sun
26559147
Lab Section:LD2
Problems
Question:Two wavesare propagatingfromtwodifferentpointsources.If the wavelength is10
meters,whatare the pathlengthsof the twowaves to make thisa conditionforconstructive
interference?Howaboutdestructiveinterference?
Solution:
For constructive interference tooccur,the propertyisthat bothpaths musteach be an integermultiple
of the wavelength,soone pathlengthcould20 metersandthe other30 meterssince bothare integer
multiplesof 10.
For destructive interference tooccur,the property isthat one path isan integermultipleof the
wavelengthwhilethe othermustbe a half integermultipleof the wavelength.Soone pathlengthcould
be 20 meterswhilethe otheris((2+0.5) x 10) = 25 meters.
Question:Calculate the beatfrequencyif aguitaristplays an80 Hz tone while hisstudentplays
a tone at 85 Hz concurrently.
Solution:
Since the amplitude of bothsoundsislarge forbothnegative andpositivepeaks,the amplitudevariation
will have the same frequencyasthe differenceof the twofrequencies.The equation:∆ω = (ω1 - ω2)/2
definesthe differencefrequency,butthe effectof thisistoregulate the amplitude.Thus,the beat
frequencyissimplythe difference of the frequencies,whichis
85 – 80 = 5 Hz.
Question:A musicteacherlistenstohergroupof studentsplaybuthearsa beatingin the
overall notes beingplayed, like asoundoscillating.Whatdoesthis suggestandwhatshould she tell her
students tostopthe beating?
Solution:
Beats,whenheardininstrumentssuch violins,harps,andguitars,oftenmeanthataninstrumentisoff
tune.Thiseffecteasilyhelpsinensuringthatall instrumentsinasystemare playedontune to prevent
discordantsounds.She shouldaskherstudentstore-tune theirinstrumentssothat all frequencies
agree witheachother.
Question:In Physityairport,passengersboardingflightsand workers there complainedabout
hearinga beatingnoise rightbefore anannouncementonthe speakersystem.Engineersfoundthe
problem,anddiscoveredthatone partof the airport playeda380 Hz tone while the otherpartplayeda
465 Hz tone simultaneously rightbefore anannouncement,resultinginanunpleasantsound.Whatis
the beat frequencyheardbythe people inPhysityairport?
Solution:
The beat frequencyheardisthe differenceof the twofrequencies,whichis
465 – 380 = 85 Hz.

6. Yangfan(Tony) Sun
26559147
Lab Section:LD2
Works Cited
PhysicsforScientistsandEngineersAnInteractive ApproachbyHawkes,Iqbal,Mansour,Milner-
Bolotin,Williams