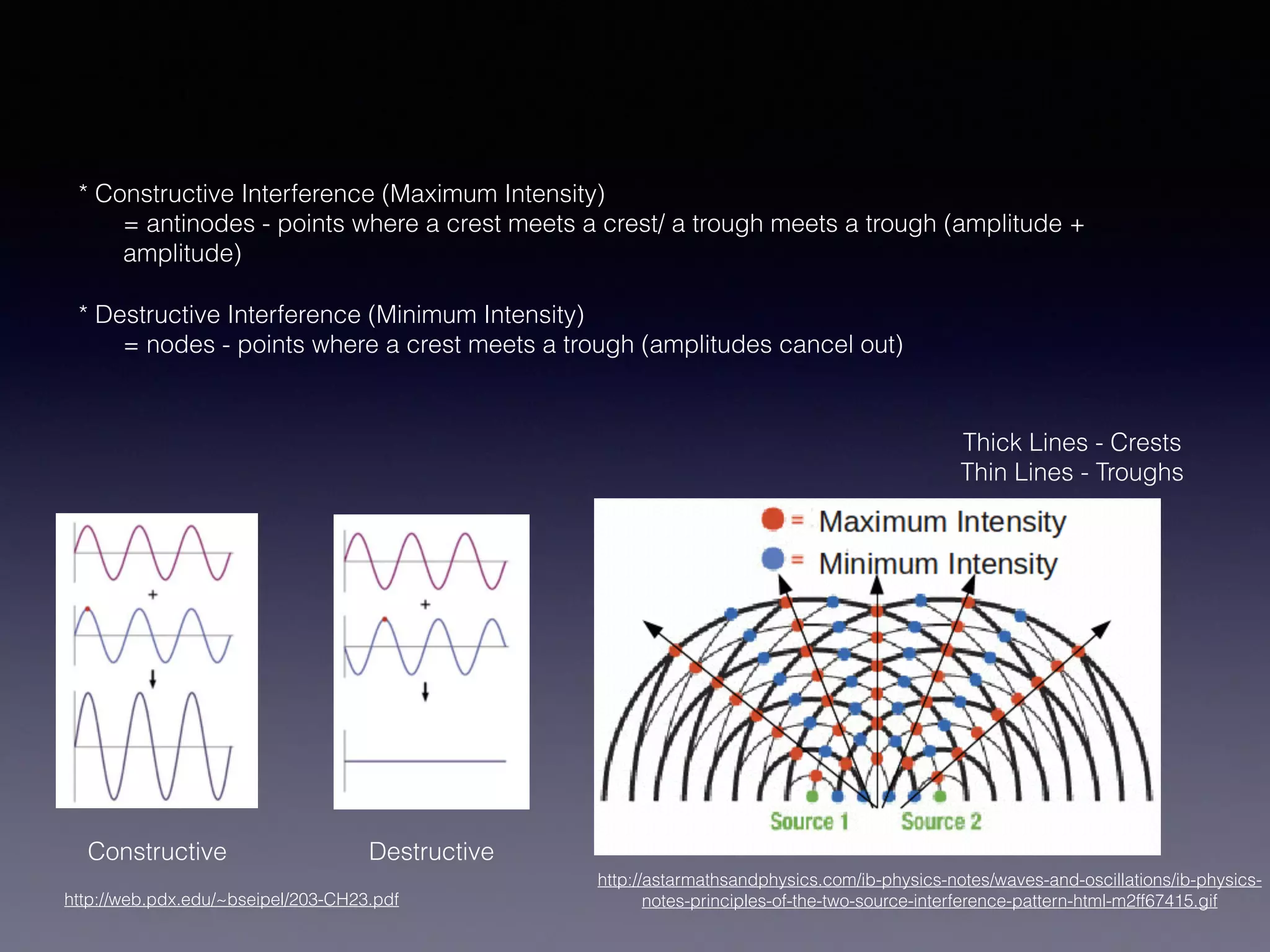
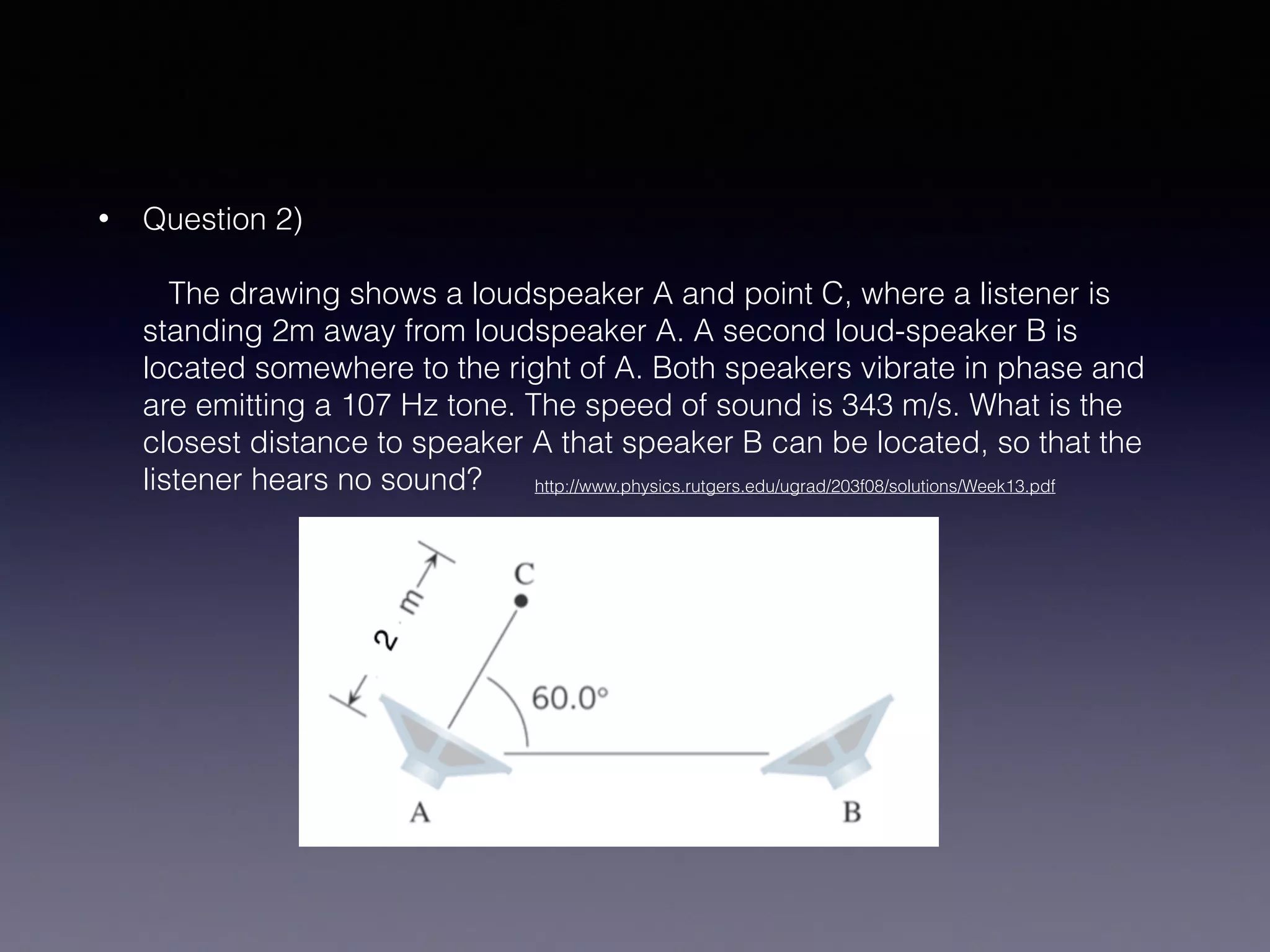
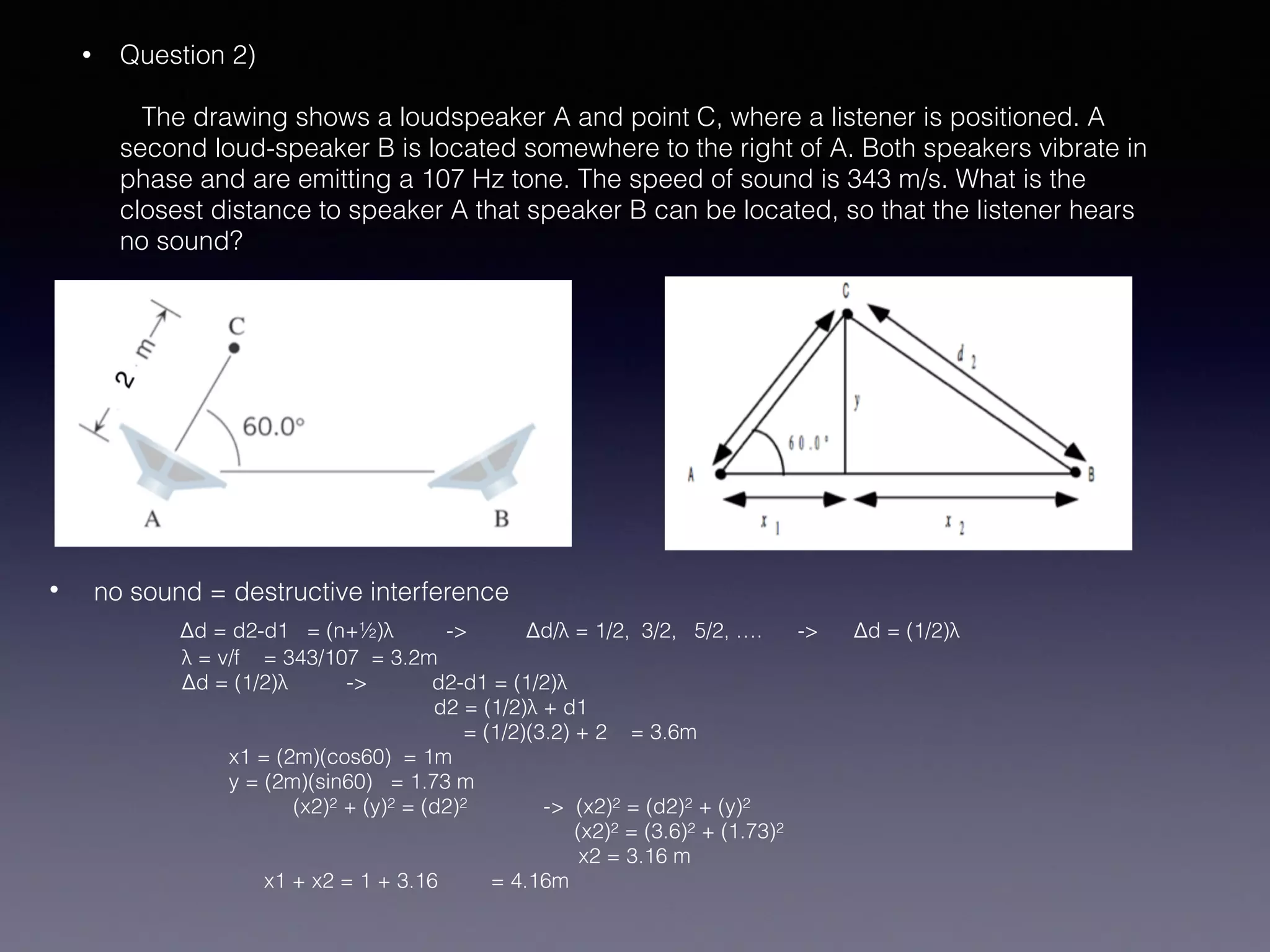
The document discusses the concepts of constructive and destructive interference of waves. It provides explanations and examples of how interference patterns arise from differences in path lengths between two sources. It also includes sample problems calculating wavelengths and frequencies that would produce maximum or minimum intensity based on information about source locations and distances. The problems demonstrate how to apply the concepts of interference to real-world scenarios involving sound waves from multiple speakers.

1. Wave Interference
PHYS 101 LO2

2. * Constructive Interference (Maximum Intensity)
= antinodes - points where a crest meets a crest/ a trough meets a trough (amplitude +
amplitude)
http://astarmathsandphysics.com/ib-physics-notes/waves-and-oscillations/ib-physics-
notes-principles-of-the-two-source-interference-pattern-html-m2ff67415.gif
Thick Lines - Crests
Thin Lines - Troughs
* Destructive Interference (Minimum Intensity)
= nodes - points where a crest meets a trough (amplitudes cancel out)
Constructive Destructive
http://web.pdx.edu/~bseipel/203-CH23.pdf

3. Path Difference for Wave Interference
• Constructive Interference
*any point that is an integer multiple of wavelengths from both sources will undergo
constructive interference
(because one period of a wavelength is 2π, any integer multiple will result in the same point)
d1 = mλ m= 1, 2, 3, …
d2 = nλ n = 1, 2, 3, …
path difference = Δd = d2-d1 =pλ p = 0, ±1, ±2, ±3 …
• Destructive Interference
*occurs when one path is an integer number of wavelength and the other is a half-
integer multiple
path difference = Δd = d2-d1 = (n+½)λ n = 0, ±1, ±2, ±3 …

4. • Question 1)
Two identical speakers, A and B, are in phase with one another.
Speaker A is positioned 10.5m directly to the north of speaker B. A person
listens to the speakers at a distance d= 4.45m directly in front of speaker
B. The speed of sound is 343 m/s.
a) What is the lowest frequency that gives minimum signal at the
person’s ear?
b) What is the second lowest frequency that gives minimum signal
at the person’s ear?
c) What is the lowest frequency that gives maximum signal at the
person’s ear?

5. • Solution 1)
Two identical speakers, A and B, are in phase with one another.
Speaker A is positioned 4.5m directly to the north of speaker B. A person
listens to the speakers at a distance d= 7.45m directly in front of speaker
B. The speed of sound is 343 m/s.
a) What is the lowest frequency that gives minimum signal at the
person’s ear?
minimum signal = destructive interference
Δd = d2-d1 = (n+½)λ -> Δd/λ = 1/2, 3/2, 5/2, …. (n=0,1,2,3,…)
path difference - d2= 8.7m
d2 - d1 = 8.7 m - 7.45m = 1.25 m
λ=v/f (f*d)/v = 1/2
f = (1/2)(v/d)
(1/2)(343/1.25) = 137.2 Hz
b) What is the second lowest frequency that gives minimum signal
at the person’s ear?
(f*d)/v = 3/2
f = (3/2)(343/1.25) = 411.6 Hz
c) What is the lowest frequency that gives maximum signal at the
person’s ear?
maximum signal = constructive interference
Δd = d2-d1 = pλ -> Δd/λ = 0, 1, 2, …
(f*d)/v = 1
f = (1)(343/1.25) = 274 Hz

6. • Question 2)
The drawing shows a loudspeaker A and point C, where a listener is
standing 2m away from loudspeaker A. A second loud-speaker B is
located somewhere to the right of A. Both speakers vibrate in phase and
are emitting a 107 Hz tone. The speed of sound is 343 m/s. What is the
closest distance to speaker A that speaker B can be located, so that the
listener hears no sound? http://www.physics.rutgers.edu/ugrad/203f08/solutions/Week13.pdf

7. • Question 2)
The drawing shows a loudspeaker A and point C, where a listener is positioned. A
second loud-speaker B is located somewhere to the right of A. Both speakers vibrate in
phase and are emitting a 107 Hz tone. The speed of sound is 343 m/s. What is the
closest distance to speaker A that speaker B can be located, so that the listener hears
no sound?
• no sound = destructive interference
Δd = d2-d1 = (n+½)λ -> Δd/λ = 1/2, 3/2, 5/2, …. -> Δd = (1/2)λ
λ = v/f = 343/107 = 3.2m
Δd = (1/2)λ -> d2-d1 = (1/2)λ
d2 = (1/2)λ + d1
= (1/2)(3.2) + 2 = 3.6m
x1 = (2m)(cos60) = 1m
y = (2m)(sin60) = 1.73 m
(x2)2 + (y)2 = (d2)2 -> (x2)2 = (d2)2 + (y)2
(x2)2 = (3.6)2 + (1.73)2
x2 = 3.16 m
x1 + x2 = 1 + 3.16 = 4.16m