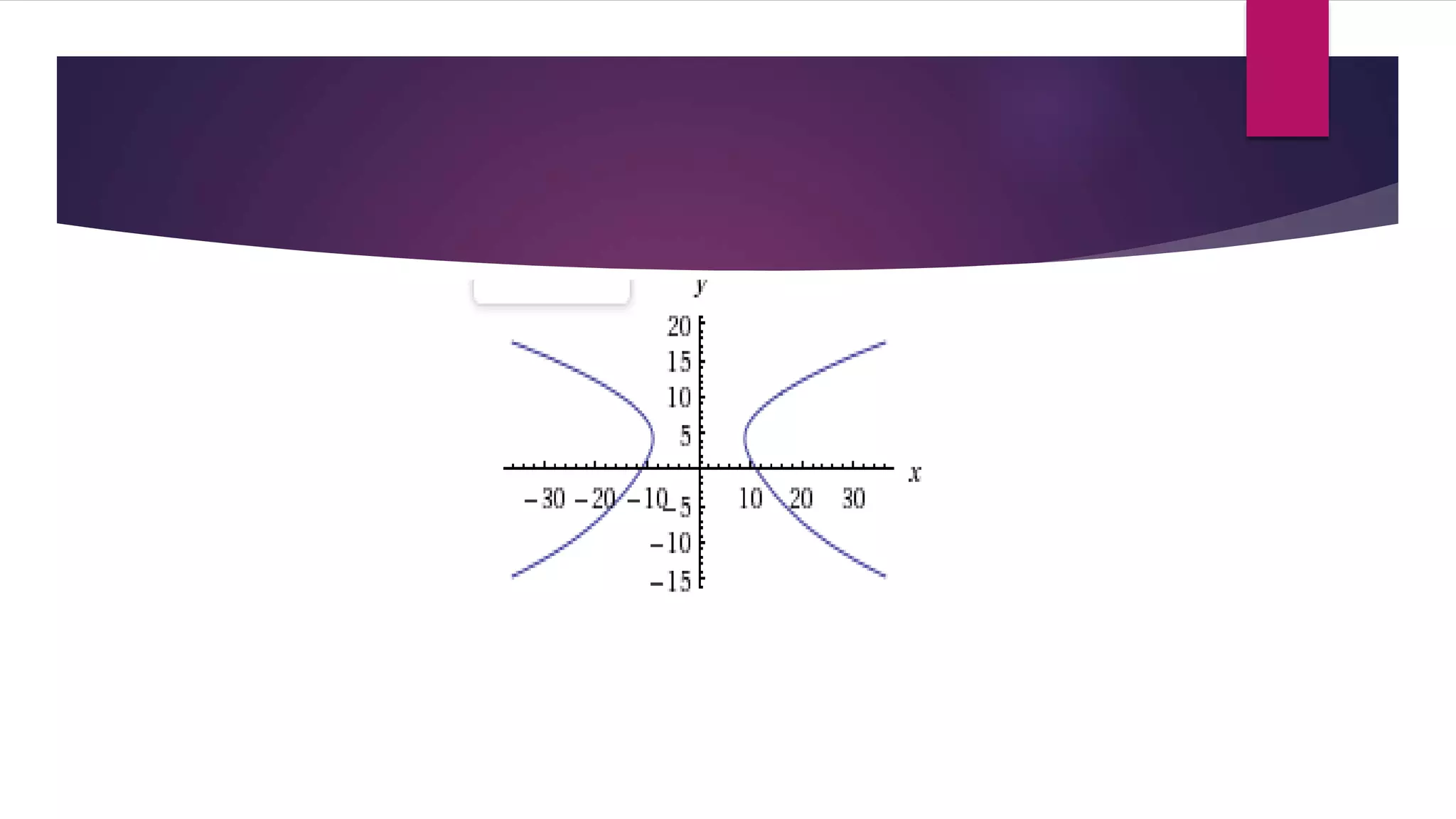
This document discusses wave interference patterns produced by two point sources of waves. It explains that when two waves are perfectly in phase, constructive interference occurs, shown as circular wave fronts. The points of constructive and destructive interference can be determined mathematically based on the path difference between the sources being equal to integer multiples of the wavelength. As an example, it analyzes the interference pattern between two boats emitting waves 80m apart, finding the point of constructive interference occurs at x = -8.90995 due to the symmetry of the setup.

1. Interference
STUDYING WAVE PATTERNS

2. Interference and 3-D waves
 One dimensional waves with the same frequency and wavelength have a
fixed phase
 When two waves are perfectly in phase, the two identical point sources
cancel out and constructive interference is produced
 Spherical wave fronts are produced by the source
 The two points at which two waves interfere constructively can be
determined mathematically

3. Understanding Constructive Interference
 When wave fronts from two different sources meet they produce circular
waves characterized by a collection of anti-nodal and nodal lines
 Waves sources with similar frequencies will have the anti-nodal lines in the
center of the pattern
 Two wave crests that have travelled a distance can be measured by the
following equation:
PD= |𝑆1A - 𝑆2A |

4. How Spherical Wave fronts are Produced
 Points on the wave which are integer multiples of wavelengths undergo
constructive interference
 Path lengths are defined as 𝑑 𝑛 where n denotes the number of path
lengths
 The path difference between two sources must be an integer multiple of
the wavelength
𝑑2 - 𝑑1 = (n-m)𝜆
p = 0, ±1, ±2, ±3, …

5.  Spatial Variations can be described as a function of r, which is the
distance from the source
 The wave function of a spherical wave can be expressed as:
s(r,t) = 𝑠 𝑚 r cos kr − ω𝑡 + 𝜑
ω = an integer multiplied by t
φ = one − dimensional wavelength

6.  Wave fronts that spread over a larger area propagate outwards and the
amplitude decreases as r increases
 (k𝑑2 - 𝜔𝑡) − 𝑘 𝑑1 − 𝜔𝑡 = 𝑘(𝑑2- 𝑑1) = n2𝜋
Therefore,
𝑑2- 𝑑1 = n(2𝜋/k) = n𝜆
When the path difference is a half-integer multiple of the wavelength,
destructive interference occurs:
(2n + ½) 𝜆 = (n + ½) 𝜆

7. Problem 1
 2 boats are placed 80 m apart and emit waves with the same amplitude
and phase; the wavelength is 10m. Identify the points of constructive and
destructive interference.

8.  𝑑2 - 𝑑1 = (𝑥2
+ (y + 10)^2) ^ (1/2) – (x^2 – (y – 10)^2) ^ (1/2) = n𝜆
 In this problem, n𝜆 is equal to 10m. It is difficult to compute this equation
without using mathematical software. Therefore, Wolfram Alpha was used
to solve for x which is approximately -8.90995. The variable y is still very
difficult to compute and this cannot be resolved to an approximate value.

10.  This graph concludes that a plane of vertical symmetry exists and therefore
there are solutions that correspond to the path difference of wavelength
10m. Since this symmetry exists, only constructive interference exists and
this occurs at following point (compute by Wolfram Alpha):

11. References
Hawkes, Iqbal, Mansour, Milner-Bolotin, Williams. Physics for Scientists and
Engineers. 2012.
Image sources: Wolfram Alpha Computational Knowledge Engine