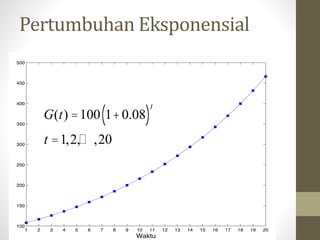
Dokumen ini membahas tentang fungsi eksponensial dan logaritma, termasuk sifat-sifat, aturan dasar, dan contoh penerapan. Terdapat latihan soal untuk menentukan nilai variabel serta aplikasi fungsi dalam pertumbuhan eksponensial. Selain itu, dokumen menjelaskan tentang penggunaan logaritma dalam menyelesaikan persamaan dan sifat-sifatnya sebagai invers dari fungsi eksponensial.