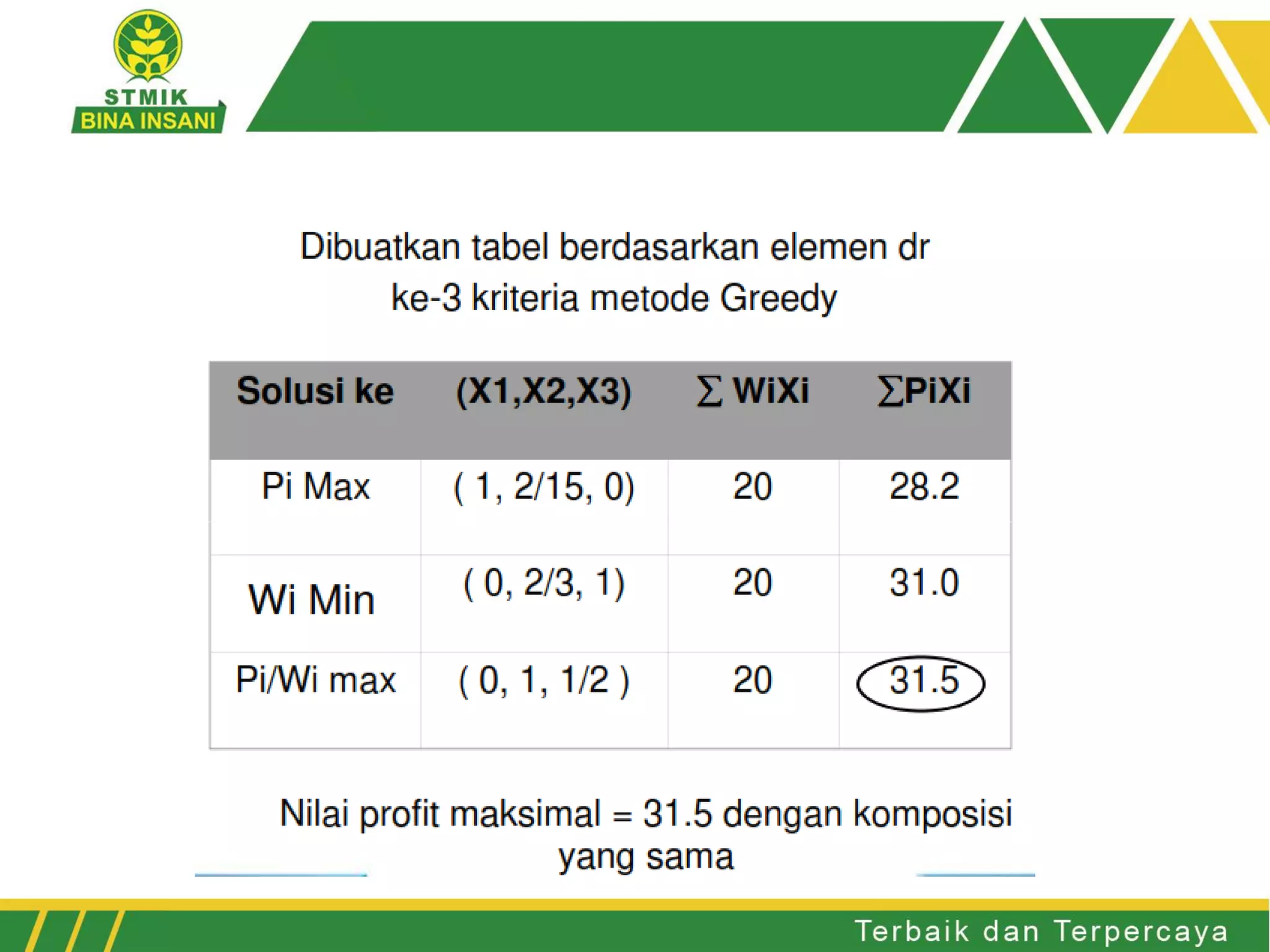
1. Algoritma greedy merupakan metode untuk memecahkan masalah optimasi secara langkah demi langkah dengan memilih solusi terbaik pada setiap langkah tanpa mempertimbangkan konsekuensi di masa depan. 2. Contoh masalah optimasi yang dibahas adalah masalah penukaran uang dan penyimpanan program komputer secara optimal menggunakan metode greedy. 3. Metode greedy juga diterapkan untuk memecahkan masalah knapsack

1. PERTEMUAN 12
Dosen : Endang Retnoningsih, M.Kom
www.endangretno.com

2. Have a Great and Blessed day…
Tahap paling sulit dari perjalanan keluar dari rasa
bersalah adalah meyakinkan diri kita bahwa kita
layak dimaafkan.

3. Pendahuluan
• Algoritma greedy merupakan metode yang paling
populer untuk memecahkan persoalan optimasi.
• Persoalan optimasi (optimization problems):
 persoalan mencari solusi optimum.
• Hanya ada dua macam persoalan optimasi:
1. Maksimasi (maximization)
2. Minimasi (minimization)

4. Contoh persoalan optimasi:
( Masalah Penukaran Uang): Diberikan uang
senilai A. Tukar A dengan koin-koin uang yang
ada. Berapa jumlah minimum koin yang
diperlukan untuk penukaran tersebut?

5. Contoh 1: tersedia banyak koin 1, 5, 10, 25
• Uang senilai A = 32 dapat ditukar dengan
banyak cara berikut:
32 = 1 + 1 + … + 1 (32 koin)
32 = 5 + 5 + 5 + 5 + 10 + 1 + 1 (7 koin)
32 = 10 + 10 + 10 + 1 + 1 (5 koin)
… dst
• Minimum: 32 = 25 + 5 + 1 + 1 (4 koin)
 Persoalan minimasi

6. • Greedy = rakus, tamak, loba, …
Prinsip greedy: “take what you can get now!”.
• Algoritma greedy membentuk solusi langkah per langkah
(step by step).
• Pada setiap langkah, terdapat banyak pilihan yang perlu
dieksplorasi.
• Oleh karena itu, pada setiap langkah harus dibuat
keputusan yang terbaik dalam menentukan pilihan.
METODE GREEDY

7. • Algoritma greedy adalah algoritma yang memecahkan
masalah langkah per langkah;
pada setiap langkah:
1. Mengambil pilihan yang terbaik yang dapat diperoleh
pada saat itu tanpa memerhatikan konsekuensi ke
depan(prinsip “take what you can get now!”)
2. berharap bahwa dengan memilih optimum lokal pada
setiap langkah akan berakhir dengan optimum global.
METODE GREEDY

8. • Tinjau masalah penukaran uang:
Strategi greedy:
Pada setiap langkah, pilihlah koin dengan nilai terbesar
dari himpunan koin yang tersisa.
• Misal: A = 32, koin yang tersedia: 1, 5, 10, dan 25
Langkah 1: pilih 1 buah koin 25 (Total = 25)
Langkah 2: pilih 1 buah koin 5 (Total = 25 + 5 = 30)
Langkah 3: pilih 2 buah koin 1 (Total = 25+5+1+1= 32)
• Solusi: Jumlah koin minimum = 4 (solusi optimal!)

9. • Untuk sistem mata uang algoritma greedy selalu
memberikan solusi optimum.
• Contoh: Uang $6,39 ditukar dengan uang kertas (bill)
dan koin sen (cent), kita dapat memilih:
- Satu buah uang kertas senilai $5
- Satu buah uang kertas senilai $1
- Satu koin 25 sen
- Satu koin 10 sen
- Empat koin 1 sen
$5 + $1 + 25c + 10c + 1c + 1c + 1c + 1c = $6,39
 Persoalan Optimasi

10. Contoh : Tiga pelanggan dengan
t1 = 5, t2 = 10, t3 = 3,
Enam urutan pelayanan yang mungkin:
============================================
Urutan T
============================================
1, 2, 3 : 5 + (5 + 10) + (5 + 10 + 3 ) = 38
1, 3, 2 : 5 + (5 + 3) + (5 + 3 + 10) = 31
2, 1, 3 : 10 + (10 + 5) + (10 + 5 + 3) = 43
2, 3, 1 : 10 + (10 + 3) + (10 + 3 + 5) = 41
3, 1, 2 : 3 + (3 + 5) + (3 + 5 + 10) = 29  (optimal)
3, 2, 1 : 3 + (3 + 10) + (3 + 10 + 5) = 34
============================================

11. 1. Optimal Storage On Tapes Problem
• Permasalahan Bagaimana mengoptimalisasi memory
dalam komputer agar data yang disimpan dapat
termuat dgn optimal.
• Misalkan terdapat hard disk berkapasitas 200 Gb,
dimana HD tsb akan diinstal SW (Windows 7, Linux
dan C++) Bagaimana cara menyimpan SW agar dapat
memenuhi HD secara optimal.
• Cara penyimpanan adalah penyimpanan secara
terurut (sequential).
11

12. Contoh
• Misal terdapat 3 buah program(n=3) yg
masing-masing mempunyai panjang program
(L1,L2,L3)=(5,10,3).
• Tentukan urutan penyimpanannya scr
berurutan (sequential) agar optimal....!
L1 L2 L3
12

13. Penyelesaiannya :
• Dari 3 program tersebut akan didapat 6 buah
kemungkinan order, yg didapat dr nilai faktorial , 3!
(ingat faktorial n!).
Optimal
13

14. 2. KNAPSACK Problem
• Knapsack dapat diartikan sebagai karung, kantung, atau
buntilan.
• Karung digunakan untuk memuat sesuatu.
• Dan tentunya tidak semua objek dapat ditampung di
dalam karung. Karung tersebut hanya dapat menyimpan
beberapa objek dengan total ukurannya (weight) lebih
kecil atau sama dengan ukuran kapasitas karung.
• Tujuan ingin mendapatkan profit yang maksimal.
14

15. Masalah :
• Bagamana obyek-obyek tersebut dimuat /
• dimasukan kedalam ransel (knapsack) yg
• mempunyai kapasitas maks. = M.
• Sehingga timbul permasalahan sbb:
– Jika semua obyek harus dimuat kedalam ransel maka
berapa bagian dr setiap obyek yg ada dapat dimuat
kedalam ransel sedemikian shg nilai maks. & sesuai dgn
kapasitas ransel ?

16. • Konsep dr kriteria yg ditawarkan oleh metode
Greedy yaitu :
– Pilih obyek (barang) dengan nilai Profit(Pi) maximal
atau terbesar
– Pilih obyek (barang) dengan berat Weight (Wi)
minimal dahulu.
– Pilih obyek (barang) dgn perbandingan nilai & berat
yaitu Pi/Wi yang terbesar.
3. Greedy dengan Kriteria

24. 1.Diket kapasitas sebuah tas(M)=15 Kg
• w1 = 7; p1 = 7
• w2 = 6; p2 = 1
• w3 = 18; p3 = 4
Selesaikan dengan metode greedy yaitu dengan
kriteria perhitungan greedy!

25. 2.Diket Kapasitas knapsack K = 100, n=6
w1 = 100; p1 = 40; w2 = 50; p2 = 35;
w3 = 45; p3 = 18; w4 = 20; p4 = 4;
w5 = 10; p5 = 10; w6 = 5; p6 = 2
Selesaikan dengan metode greedy yaitu dengan
kriteria perhitungan greedy!