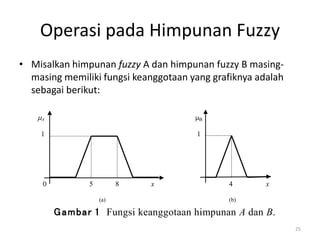
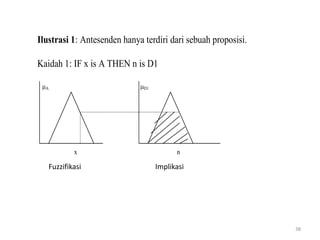
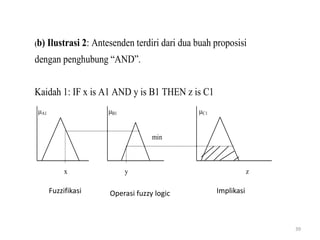
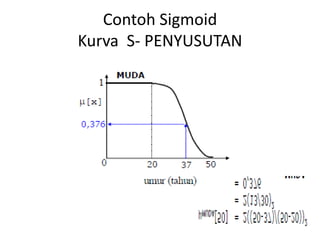
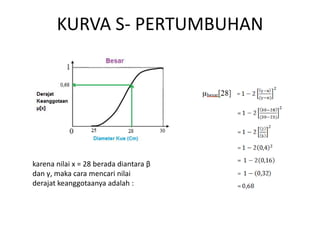
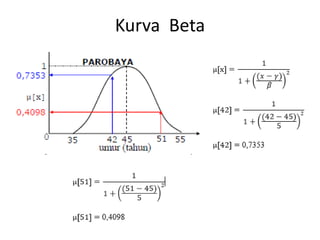
Operator himpunan fuzzy dan kaidah fuzzy digunakan untuk mengevaluasi keanggotaan beberapa karyawan ke dalam kategori umur dan tinggi tertentu. Fungsi keanggotaan umur dan tinggi digambarkan, kemudian dievaluasi apakah masing-masing karyawan termasuk kategori parobaya, tinggi, atau keduanya.

1. Operator Himpunan Fuzzy
Pertemuan Ke-3

2. Agenda
• Review Fungsi Keanggotaan
• Operator Himpunan Fuzzy untuk Operasi
• Kaidah Fuzzy (Fuzzy Rule’s)
• Evaluasi

3. REVIEW FUNGSI KEANGGOTAAN
• Linear
• Segitiga
• Trapesium
• Sigmoid
• Gauss
• Beta

4. LINIER
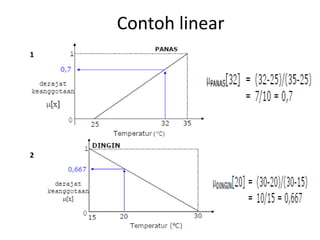
• Pada representasi linear, pemetaan input ke
derajat keanggotannya digambarkan sebagai
suatu garis lurus. Bentuk ini paling sederhana dan
menjadi pilihan yang baik untuk mendekati suatu
konsep yang kurang jelas.Ada 2 keadaan
himpunan fuzzy yang linear. Pertama, kenaikan
himpunan dimulai pada nilai domain yang
memiliki derajat keanggotaan nol [0] bergerak ke
kanan menuju ke nilai domain yang memiliki
derajat keanggotaan lebih tinggi .

5. Grafik Fungsi Linier

6. Contoh linear
1
2

7. SEGITIGA
• Kurva Segitiga pada dasarnya merupakan gabungan antara 2 garis
(linear)
Grafik Fungsi Segitiga

8. Contoh Segitiga

9. TRAPESIUM
• Kurva trapesium pada dasarnya seperti bentuk segitiga, hanya saja
ada beberapa titik yang memiliki nilai keanggotaan 1

10. Contoh Trapesium

11. KURVA PI

12. SIGMOID
Titik
Infleksi

13. SIGMOID / KURVA-S

14. Contoh Sigmoid
Kurva S- PENYUSUTAN

15. KURVA S- PERTUMBUHAN
karena nilai x = 28 berada diantara β
dan γ, maka cara mencari nilai
derajat keanggotaanya adalah :

16. BETA

17. Kurva Beta

18. EVALUASI Pertemuan ke -3
• Hitung dengan rumus segitiga untuk mencari
bilangan fuzzy jika :
Diketahui :
a = 10, b = 15, c = 30
Hitung nilai fuzzy berikut :
1) X= 5 3) X=20
2) X= 12 4) X= 35

19. EVALUASI Pertemuan ke -3
• Hitung dengan rumus trapesium untuk
mencari bilangan fuzzy jika :
Diketahui :
a = 10, b = 15, c = 18, d = 30
Hitung nilai fuzzy berikut :
1) X= 5 3) X=20
2) X= 12 4) X= 35

20. EVALUASI Pertemuan ke -3
• Hitung dengan rumus trapesium untuk
mencari bilangan fuzzy jika :
Diketahui :
a = 10, b = 15, c = 18, d = 30
Hitung nilai fuzzy berikut :
1) X= 5 3) X=20
2) X= 12 4) X= 35

22. OPERATOR HIMPUNAN FUZZY
Pertemuan Minggu Ke -4

23. Operator Pada Himpunan Fuzzy
• Operator Himpunan fuzzy menurut zadeh ada
3:
• Interseksi (AND) :
• Union (OR) :
• Komplemen (NOT) : μA’= 1- μA[x]

25. Operasi pada Himpunan Fuzzy
• Misalkan himpunan fuzzy A dan himpunan fuzzy B masing-
masing memiliki fungsi keanggotaan yang grafiknya adalah
sebagai berikut:
25
A B
1 1
0 5 8 x 4 x
(a) (b)
Gambar 1 Fungsi keanggotaan himpunan A dan B.

26. 2. Irisan
• A  B  A B = A(x)  B(x) = min(A(x), B(x))
• A  B diartikan sebagai “x dekat A dan x dekat B”.
26
A  B
1
4 5 8 x
Gambar 3 Grafik fungsi keanggotaan himpunan A  B.

27. Operator AND

29. 1. Gabungan
• A  B  A  B = A(x)  B(x) = max(A(x), B(x))
• A  B diartikan sebagai “x dekat A atau x dekat B”.
29
A  B
1
4 5 8 x
Gambar 2 Grafik fungsi keanggotaan himpunan A  B.

30. OPERATOR OR

32. 3. Komplemen
 1 – A(x)
• diartikan sebagai “x tidak dekat A”.
32
A 
A

A
A

1
0 5 8 x
Gambar 4 Grafik fungsi keanggotaan himpunan A .

35. Kaidah Fuzzy (Fuzzy’s rule)
• Bentuk kaidah fuzzy:
IF x is A THEN y is B
• Kaidah fuzzy disebut juga implikasi fuzzy
• A dan B adalah terma atau nilai lingusitik, x dan y
adalah variabel fuzzy
• “x is A” disebut antesenden atau premis
• “y is B” disebut konsekwen
35

36. • Contoh-contoh:
if permintaan is NAIK then harga is TINGGI
if temperatur is DINGIN then tekanan is SEDANG
• Antesenden dan konsekuen dimungkinkan mempunyai lebih
dari satu predikat dengan konektif and, or, dan not
• Contoh:
if pelayanan is BAGUS and makanan is ENAK THEN bonus is
BESAR
if temperatur is PANAS THEN putaran_kipas is CEPAT or
buka_ventilasi is LEBAR
36

37. Tiga tahap penginterpretasian IF-THEN rule:
1. Fuzzifikasi
Menentukan derajat keanggotaan dari variabel
masukan
2. Operasi fuzzy logic
Melakukan operasi-operasi fuzzy logic, misalnya
konektivitas AND dioperasikan dengan fungsi min
3. Implikasi
Menerapkan metdoe implikasi untuk menentukan
bentuk akhir keluaran fuzzy set. Metode implikasi yang
banyak diguankan: metode Mamdani dan metode
Sugeno (akan dijelaskan kemudian)
37

38. 38
Ilustrasi 1: Antesenden hanya terdiri dari sebuah proposisi.
Kaidah 1: IF x is A THEN n is D1
A D1
x n
Fuzzifikasi Implikasi

39. 39
(b) Ilustrasi 2: Antesenden terdiri dari dua buah proposisi
dengan penghubung “AND”.
Kaidah 1: IF x is A1 AND y is B1 THEN z is C1
A1 B1 C1
min
x y z
Fuzzifikasi Operasi fuzzy logic Implikasi

40. EVALUASI
• Sekelompok KARYAWAN, dibedakan berdasar
tinggi dan umur.
– Umur : parobaya (35-45)
– Tinggi : tinggi (135-150)
• Fungsi keanggotaan umur dengan kurva linier
naik
• Fungsi keanggotaan tinggi dengan kurva linier
turun

41. Soal :
nama umur tinggi
Ghoni 48 165
Redi 41 164
Nur khasanah 33 160
Nur hasan 30 166
Edi 29 159
a. Gambar fungsi keanggotaan masing2 orang
b. Apakah Ghoni termasuk parobaya dan tinggi ?
c. Apakah Redi termasuk parobaya atau tinggi ?
d. Apakah Nur Khasanah termasuk parobaya dan tinggi ?
e. Apakah Nur Hasan termasuk parobaya atau tinggi ?
f. Apakah Edi termasuk parobaya dan tinggi ?