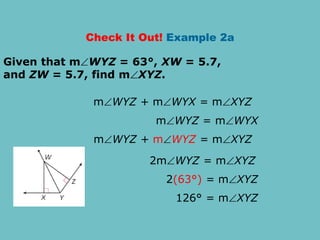
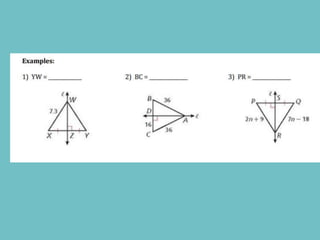
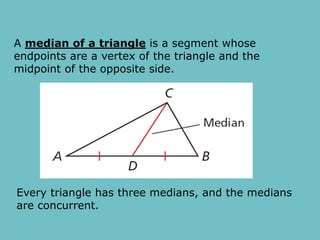
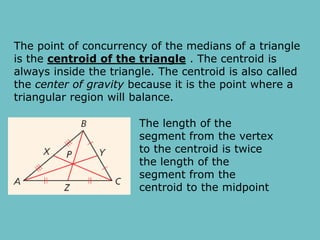
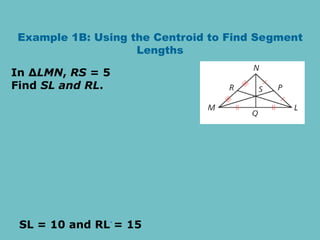
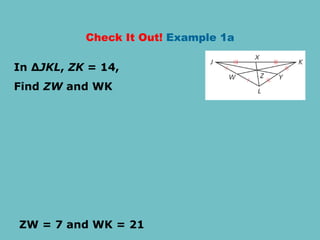
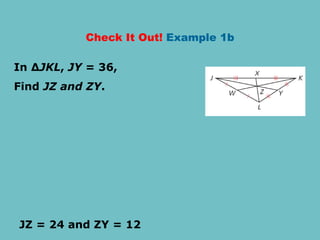
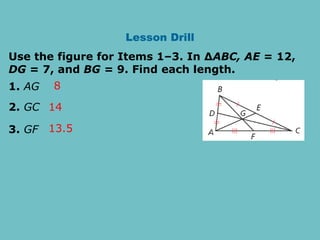
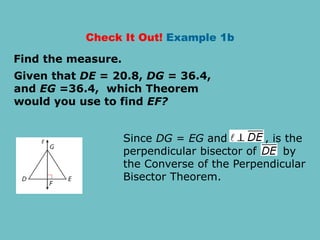
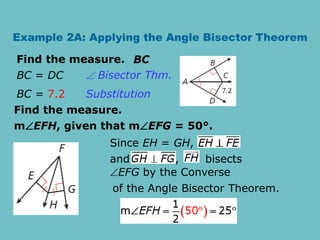
The document discusses theorems related to perpendicular and angle bisectors, providing various examples of their application to find segment measures. It explains the properties of bisectors in triangles, including the concept of medians and the centroid, which serves as the triangle's center of gravity. Additionally, it includes practice problems to reinforce understanding of these geometric principles.

1. Prove and apply theorems about
perpendicular bisectors.
Prove and apply theorems about angle
bisectors.
5.1 Objectives

3. Example 1A: Applying the Perpendicular Bisector
Theorem and Its Converse
Find each measure.
MN
MN = LN
MN = 2.6
 Bisector Thm.
Substitution

4. Example 1C: Applying the Perpendicular Bisector
Theorem and Its Converse
TU
Find each measure.
So TU = 3(6.5) + 9 = 28.5.
TU = UV  Bisector Thm.
3x + 9 = 7x – 17
9 = 4x – 17
26 = 4x
6.5 = x
Subtraction POE
Addition POE.
Division POE.
Substitution

5. Check It Out! Example 1b
Given that DE = 20.8, DG = 36.4,
and EG =36.4, which Theorem
would you use to find EF?
Find the measure.
Since DG = EG and , is the
perpendicular bisector of by
the Converse of the Perpendicular
Bisector Theorem.

6. Remember that the distance between a point and a
line is the length of the perpendicular segment from
the point to the line.

7. Example 2A: Applying the Angle Bisector Theorem
Find the measure. BC
BC = DC
BC = 7.2
 Bisector Thm.
Substitution
Find the measure.
mEFH, given that mEFG = 50°.
Since EH = GH,
and , bisects
EFG by the Converse
of the Angle Bisector Theorem.

8. Example 2C: Applying the Angle Bisector Theorem
Find mMKL.
, bisects JKL
Since, JM = LM, and
by the Converse of the Angle
Bisector Theorem.
mMKL = mJKM
3a + 20 = 2a + 26
a + 20 = 26
a = 6
Def. of  bisector
Substitution.
Subtraction POE
Subtraction POE
So mMKL = [2(6) + 26]° = 38°

9. Check It Out! Example 2a
Given that mWYZ = 63°, XW = 5.7,
and ZW = 5.7, find mXYZ.
mWYZ = mWYX
mWYZ + mWYX = mXYZ
mWYZ + mWYZ = mXYZ
2(63°) = mXYZ
126° = mXYZ
2mWYZ = mXYZ

11. Prove and apply properties of
perpendicular bisectors of a triangle.
Prove and apply properties of angle
bisectors of a triangle.
5.2 Objectives

12. The perpendicular bisector of a side of a triangle
does not always pass through the opposite
vertex.
Helpful Hint

13. A median of a triangle is a segment whose
endpoints are a vertex of the triangle and the
midpoint of the opposite side.
Every triangle has three medians, and the medians
are concurrent.

14. The point of concurrency of the medians of a triangle
is the centroid of the triangle . The centroid is
always inside the triangle. The centroid is also called
the center of gravity because it is the point where a
triangular region will balance.
The length of the
segment from the vertex
to the centroid is twice
the length of the
segment from the
centroid to the midpoint

15. Example 1B: Using the Centroid to Find Segment
Lengths
In ∆LMN, RS = 5
Find SL and RL.
.
SL = 10 and RL = 15

16. Check It Out! Example 1a
In ∆JKL, ZK = 14,
Find ZW and WK
ZW = 7 and WK = 21

17. Check It Out! Example 1b
In ∆JKL, JY = 36,
Find JZ and ZY.
JZ = 24 and ZY = 12

18. Lesson Drill
Use the figure for Items 1–3. In ∆ABC, AE = 12,
DG = 7, and BG = 9. Find each length.
1. AG
2. GC
3. GF
8
14
13.5