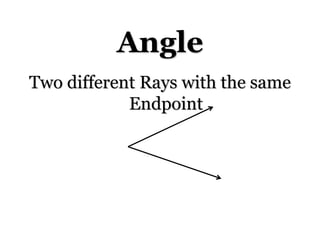
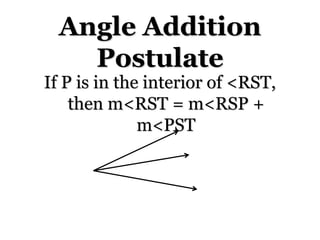
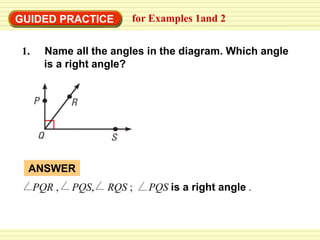
1. The document defines key angle concepts such as acute, obtuse, right, and straight angles. It also introduces the protractor and angle addition postulate. 2. The examples demonstrate how to name angles, measure angles using a protractor, find missing angle measures using the angle addition postulate, identify congruent angles, and double an angle measure when the angle is bisected. 3. The guided practice problems apply the concepts taught in the examples to find missing angle measures, identify congruent angles, and draw and label diagrams related to bisected and straight angles.

1. 1.4 Key Concepts

2. Angle
Two different Rays with the same
Endpoint

3. Sides
The Rays of the Angle

4. Vertex
The Endpoint of the Angle

5. Acute Angle
An Angle between 0° and 90 °.

6. Right Angle
An Angle that equals 90 °

7. Obtuse Angle
An Angle between 90 ° and 180 °

8. Straight Angle
An Angle that equals 180 °

9. Protractor
Postulate
The measure of an angle is equal
to the absolute value of the
difference between values of the
rays on the protractor.

10. Angle Addition
Postulate
If P is in the interior of <RST,
then m<RST = m<RSP +
m<PST

11. EXAMPLE 1 Name angles
Name the three angles in the diagram.
WXY, or YXW
YXZ, or ZXY
WXZ, or ZXW
You should not name any of these angles X
because all three angles have X as their vertex.

12. EXAMPLE 2 Measure and classify angles
Use the diagram to find the measure of the indicated
angle. Then classify the angle.
a. KHJ b. GHK c. GHJ d. GHL
SOLUTION
A protractor has an inner and
an outer scale. When you
measure an angle, check to
see which scale to use.

13. EXAMPLE 2 Measure and classify angles
a. HJ is lined up with the 0 on the inner scale of the
protractor. HK passes through 55 on the inner
scale. So, m KHJ = 55 . It is an acute angle.
o
o
o
b. HG is lined up with the 0 on the outer scale and
HK passes through 125 on the outer scale. So, m
GHK = 125 . It is an obtuse angle.
o
o
o
c. m GHJ = 180.
It is a straight angle.
o
d. m GHL= 90.
It is a right angle.
o

14. GUIDED PRACTICE for Examples 1and 2
1. Name all the angles in the diagram. Which angle
is a right angle?
PQR , PQS, RQS ; PQS is a right angle .
ANSWER

15. GUIDED PRACTICE for Examples 1and 2
2. Draw a pair of opposite rays. What type of angle
do the rays form?
ANSWER
Straight Angle

16. EXAMPLE 3 Find angle measures
o
ALGEBRA Given that m LKN =145 , find m LKM
and m MKN.
SOLUTION
STEP 1
Write and solve an equation to find the value of x.
m LKN = m LKM + m MKN Angle Addition Postulate
Substitute angle measures.
145 = 6x + 7 Combine like terms.
Subtract 7 from each side.
138 = 6x
Divide each side by 6.
23 = x
145 = (2x + 10) + (4x – 3)
o o
o

17. EXAMPLE 3 Find angle measures
STEP 2
Evaluate the given expressions when x = 23.
m LKM = (2x + 10)° = (2 23 + 10)° = 56°
m MKN = (4x – 3)° = (4 23 – 3)° = 89°
So, m LKM = 56° and m MKN = 89°.
ANSWER

18. GUIDED PRACTICE for Example 3
Find the indicated angle measures.
3. Given that KLM is a straight angle, find m KLN
and m NLM.
ANSWER 125°, 55°

19. GUIDED PRACTICE for Example 3
4. Given that EFG is a right angle, find m EFH
and m HFG.
ANSWER 60°, 30°

20. EXAMPLE 4 Identify congruent angles
The photograph shows some of the angles
formed by the ropes in a trapeze apparatus. Identify the
congruent angles. If m DEG = 157° ,what is m GKL?
Trapeze
SOLUTION There are two pairs of congruent angles:
DEF JKL and DEG GKL.
~ ~
Because  DEG GKL, DEG = m GKL.
So, m GKL = 157°.
~

21. GUIDED PRACTICE for Example 4
5. Identify all pairs of congruent angles in the diagram.
Use the diagram shown.
T and S, P and R.
ANSWER

22. GUIDED PRACTICE for Example 4
6. In the diagram, m PQR = 130 , m QRS = 84, and
m TSR = 121 . Find the other angle measures in
the diagram.
o
o
o
Use the diagram shown.
m PTS = 121°, m QPT = 84°
ANSWER

23. SOLUTION
EXAMPLE 5 Double an angle measure
In the diagram at the right, YW bisects XYZ, and
m XYW = 18. Find m XYZ.
o
By the Angle Addition Postulate, m
XYZ = m XYW + m WYZ. Because YW bisects XYZ
you know that XYW WYZ.
~
So, m XYW = m WYZ, and you can write
m XYZ = m XYW + m WYZ = 18° + 18° = 36°.

24. GUIDED PRACTICE for Example 5
7. Angle MNP is a straight angle, and NQ bisects
MNP. Draw MNP And NQ . Use arcs to mark
the congruent angles in your diagram, and give
the angle measures of these congruent angles.
90°
ANSWER