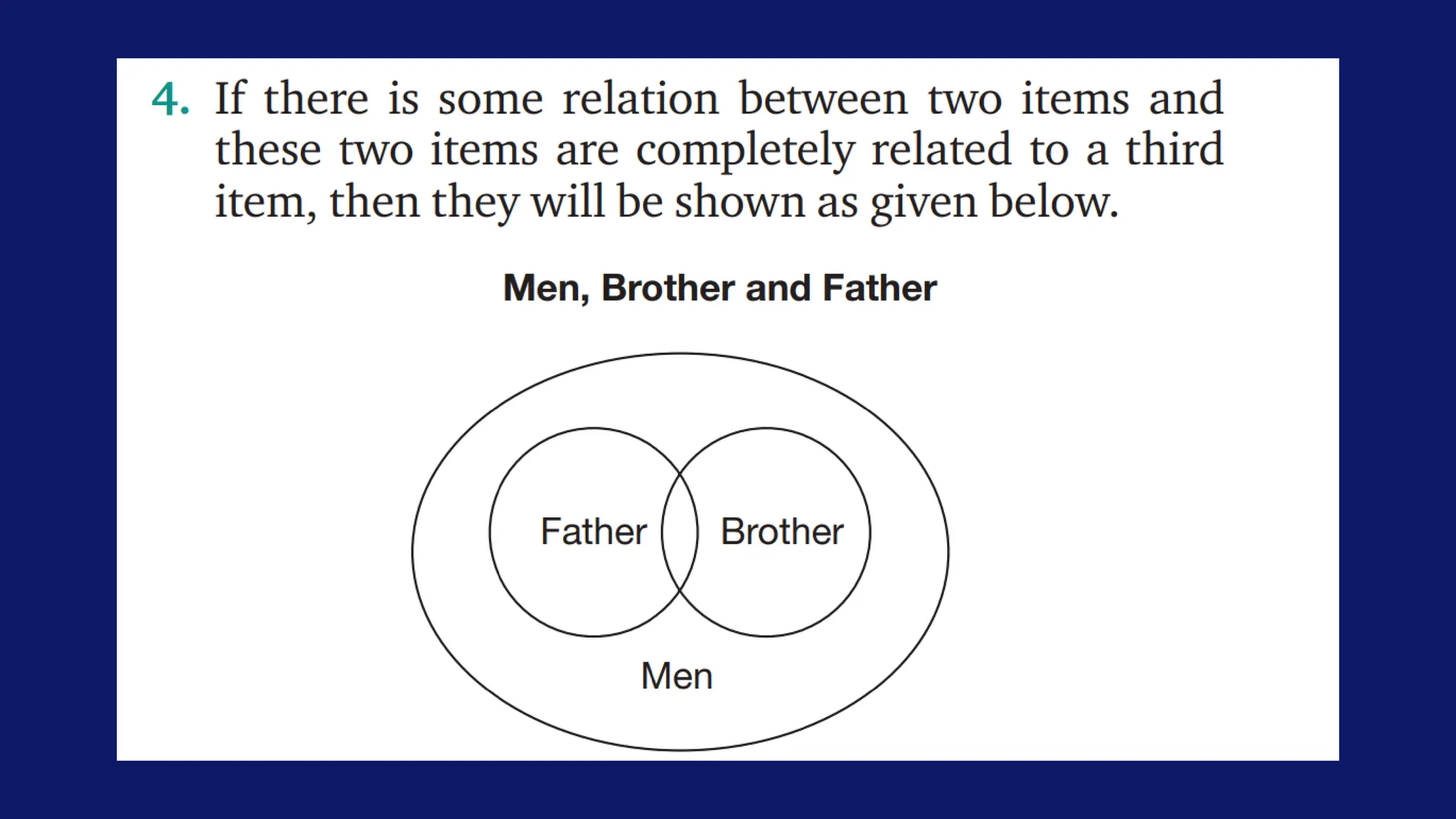
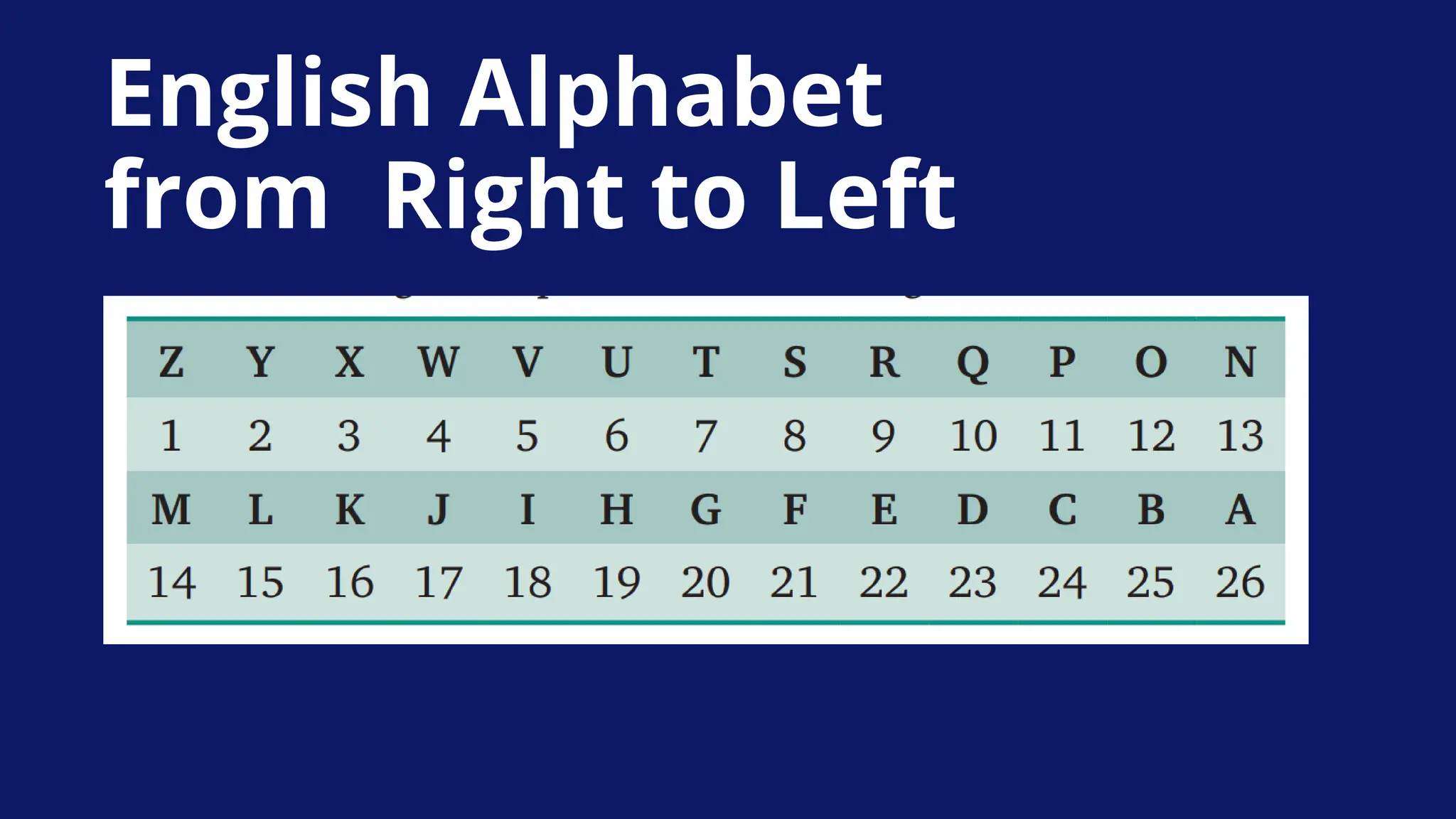
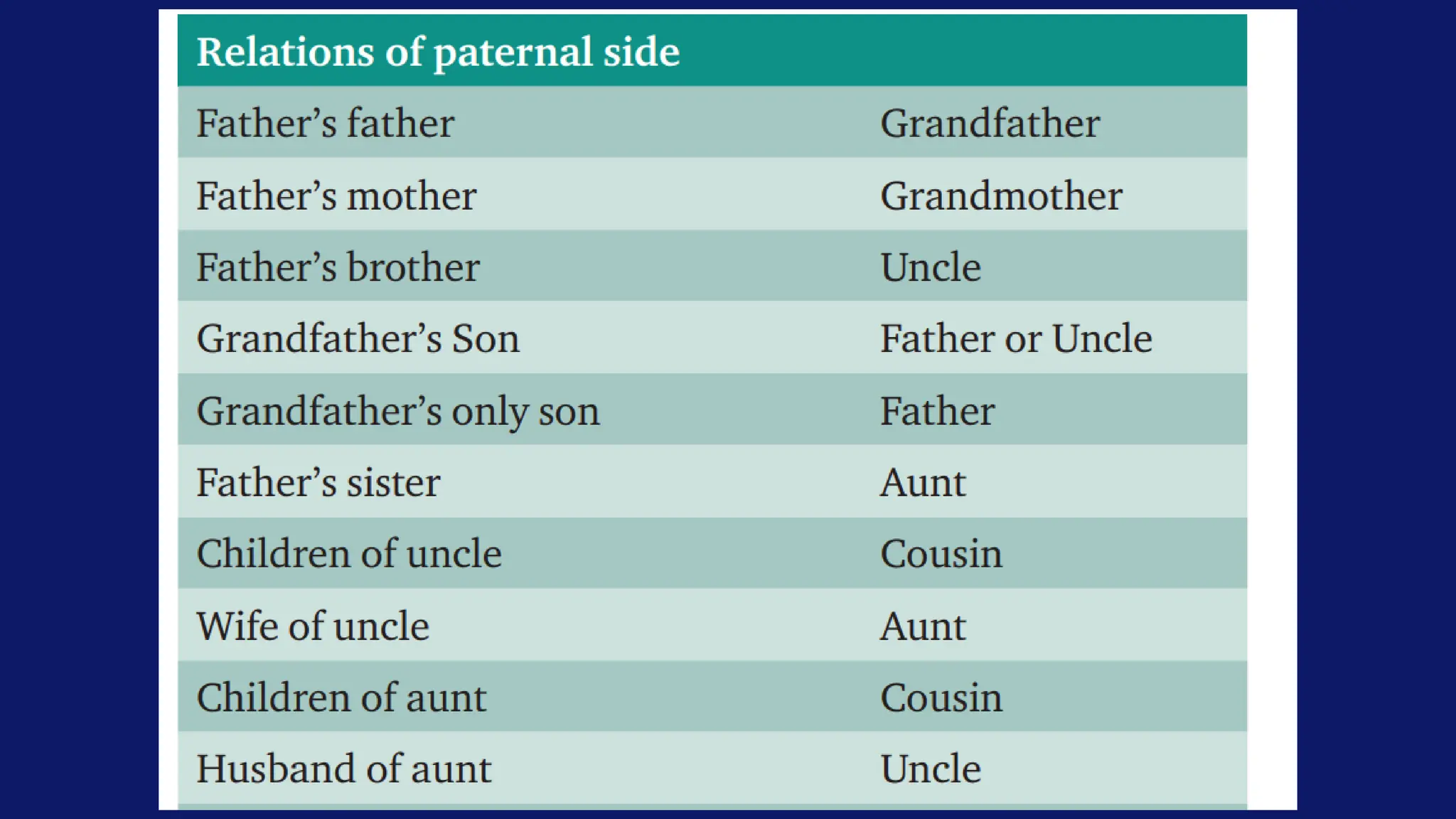
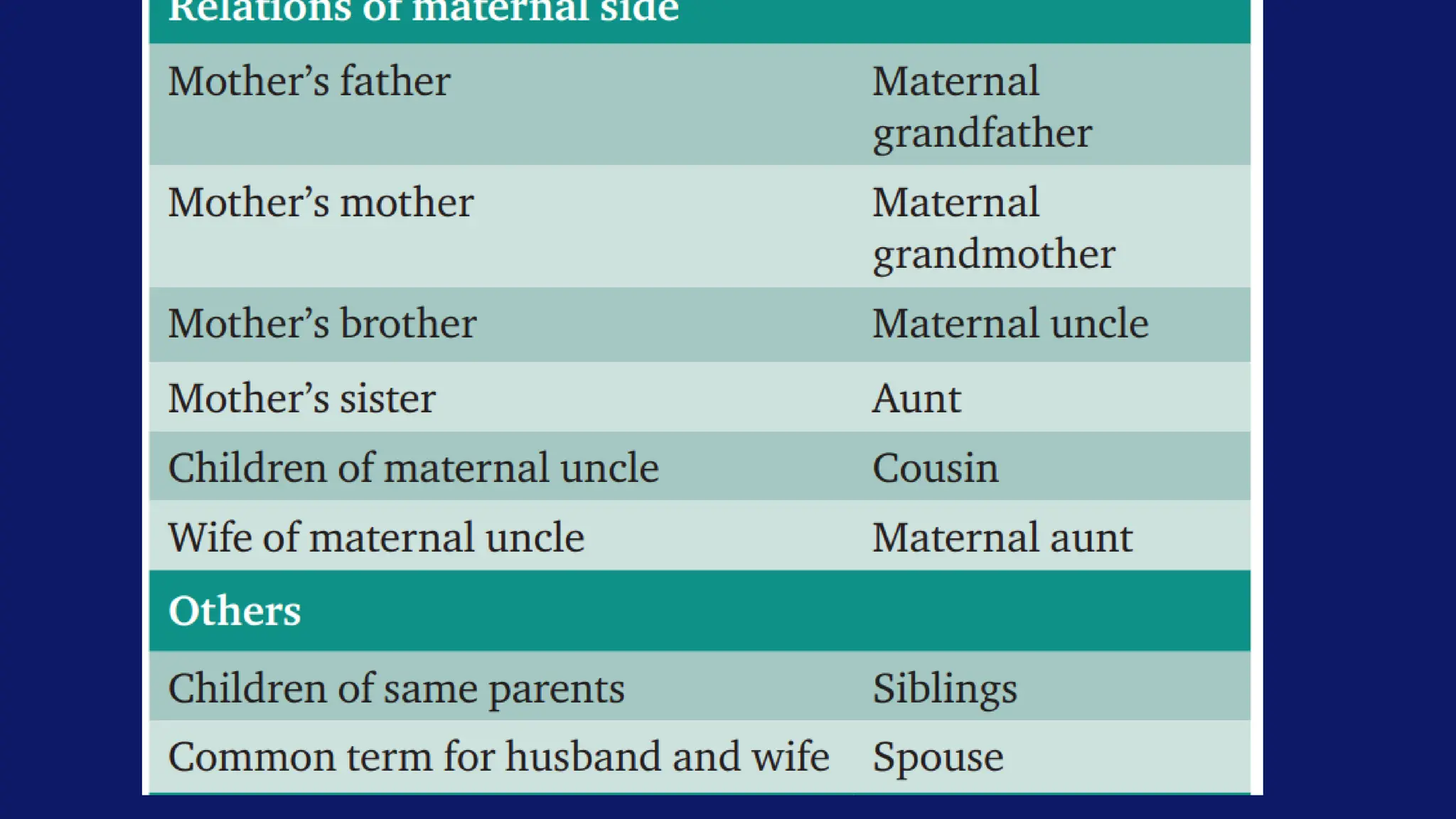
The document covers various types of reasoning and mathematical aptitude useful for UGC NET Paper 1. It details different reasoning methods such as deductive, inductive, analogical, and abductive reasoning, and explains concepts related to number series, letter series, and coding and decoding techniques. Additionally, it includes examples of problem-solving involving number and letter sequences, critical thinking, and mathematical concepts like fractions and ratios.
































































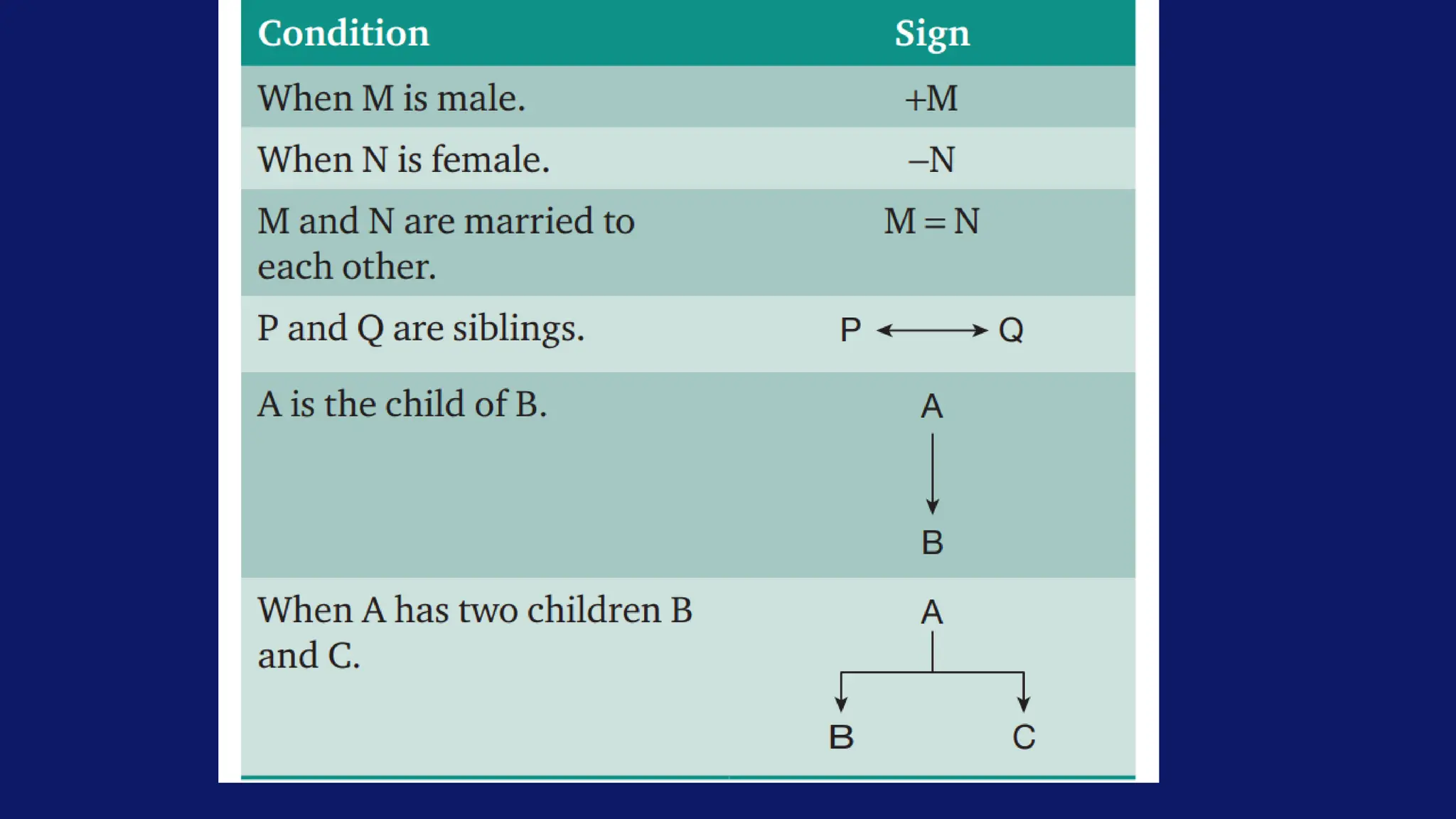













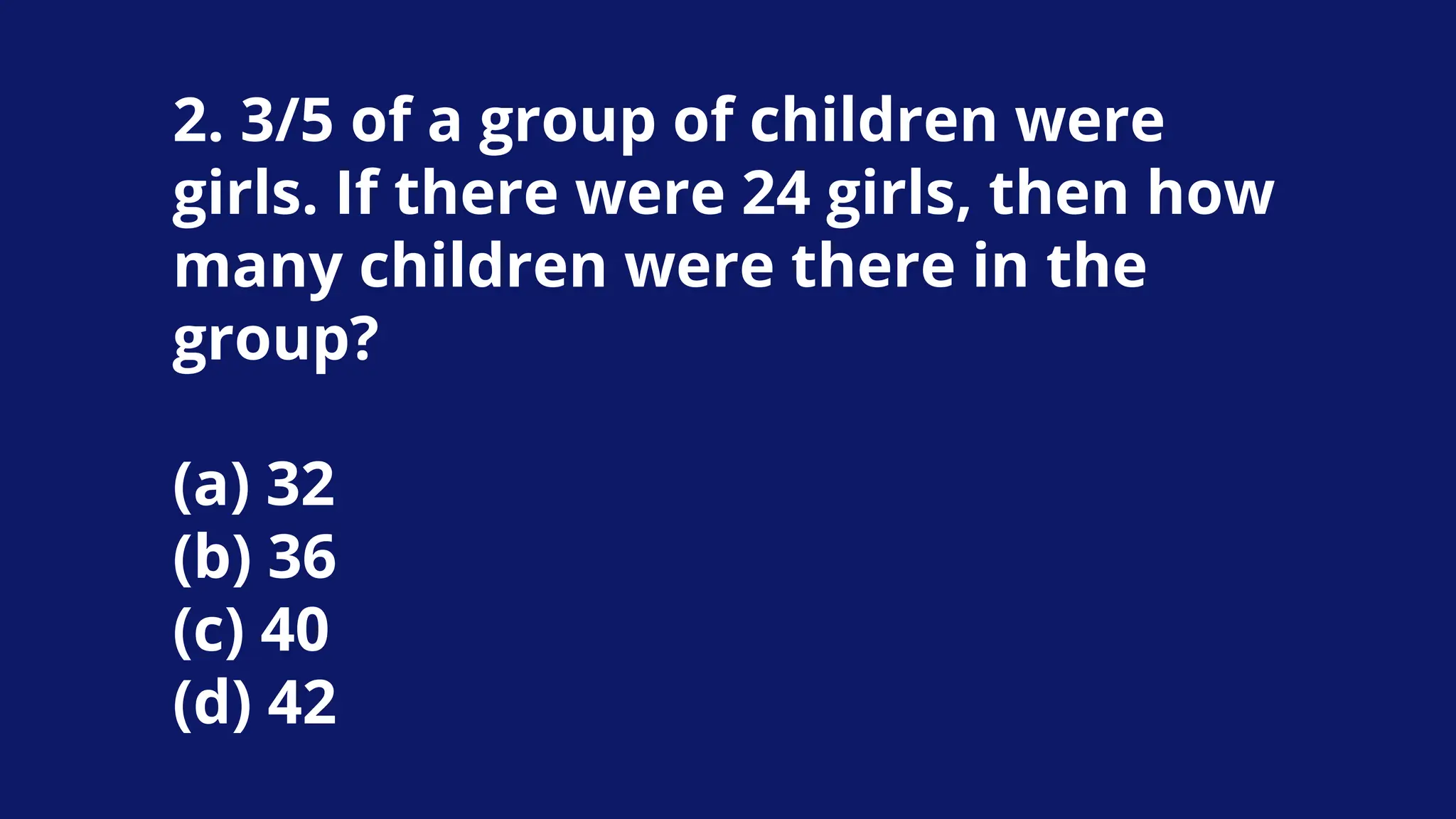
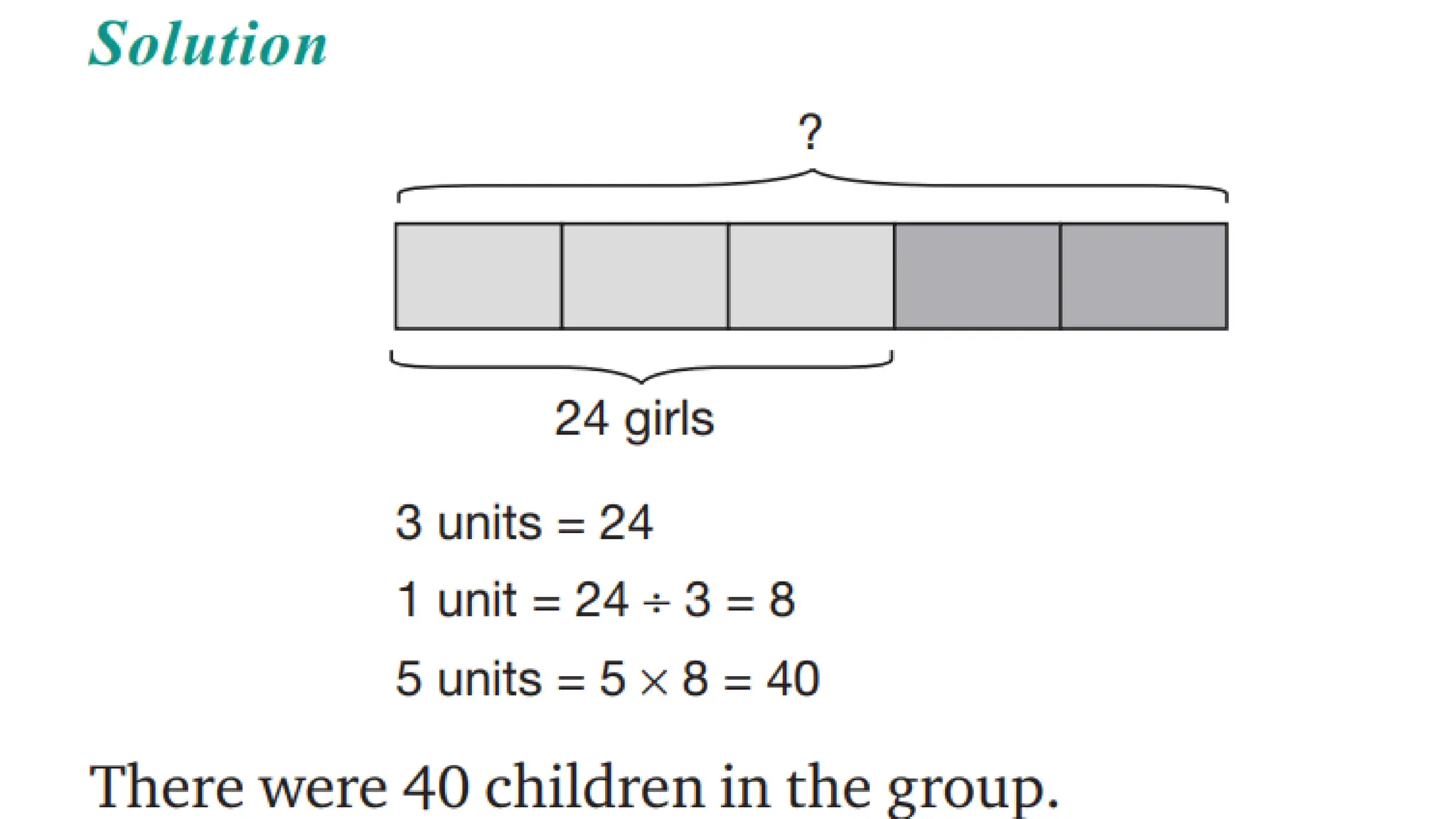









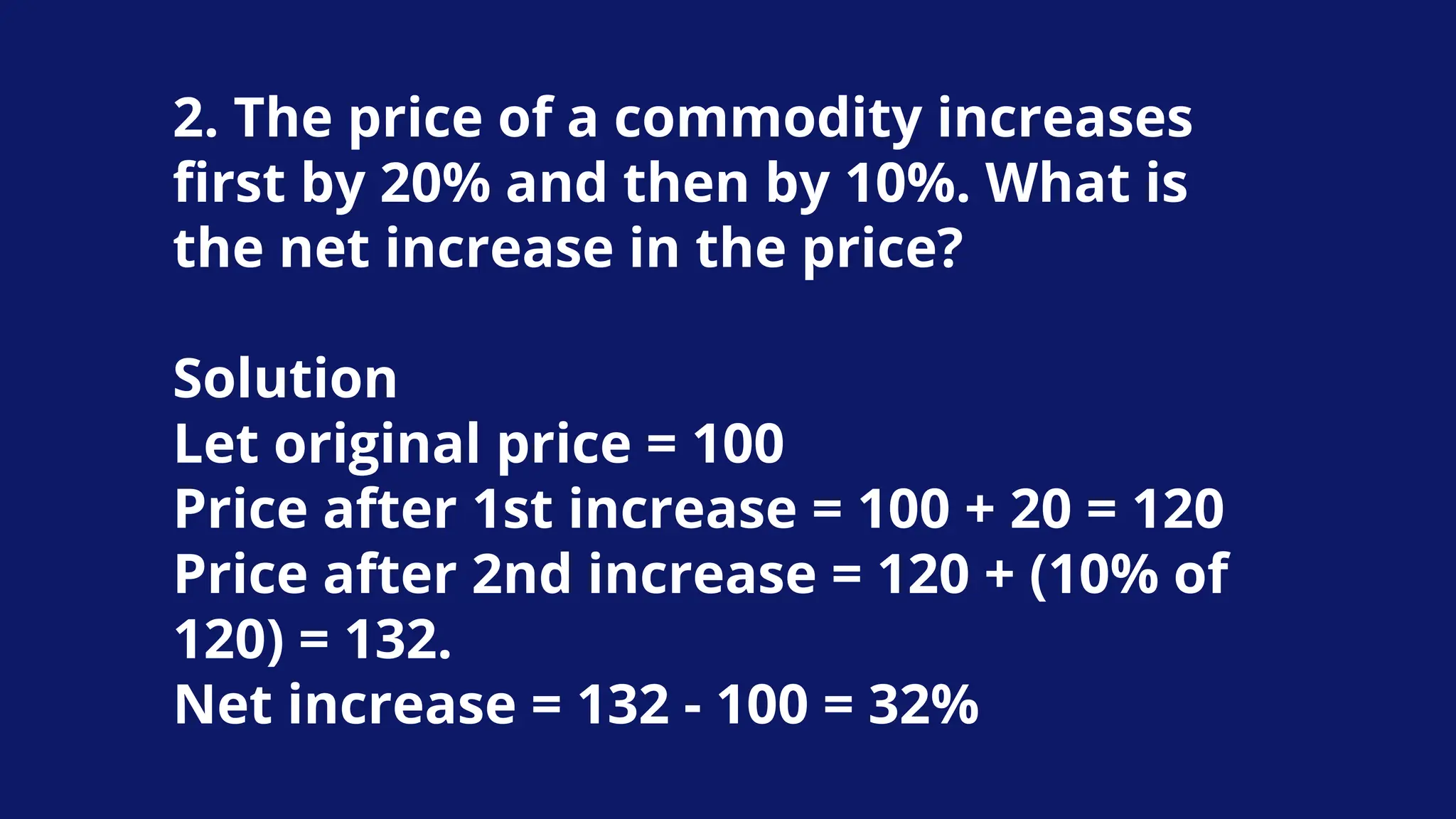


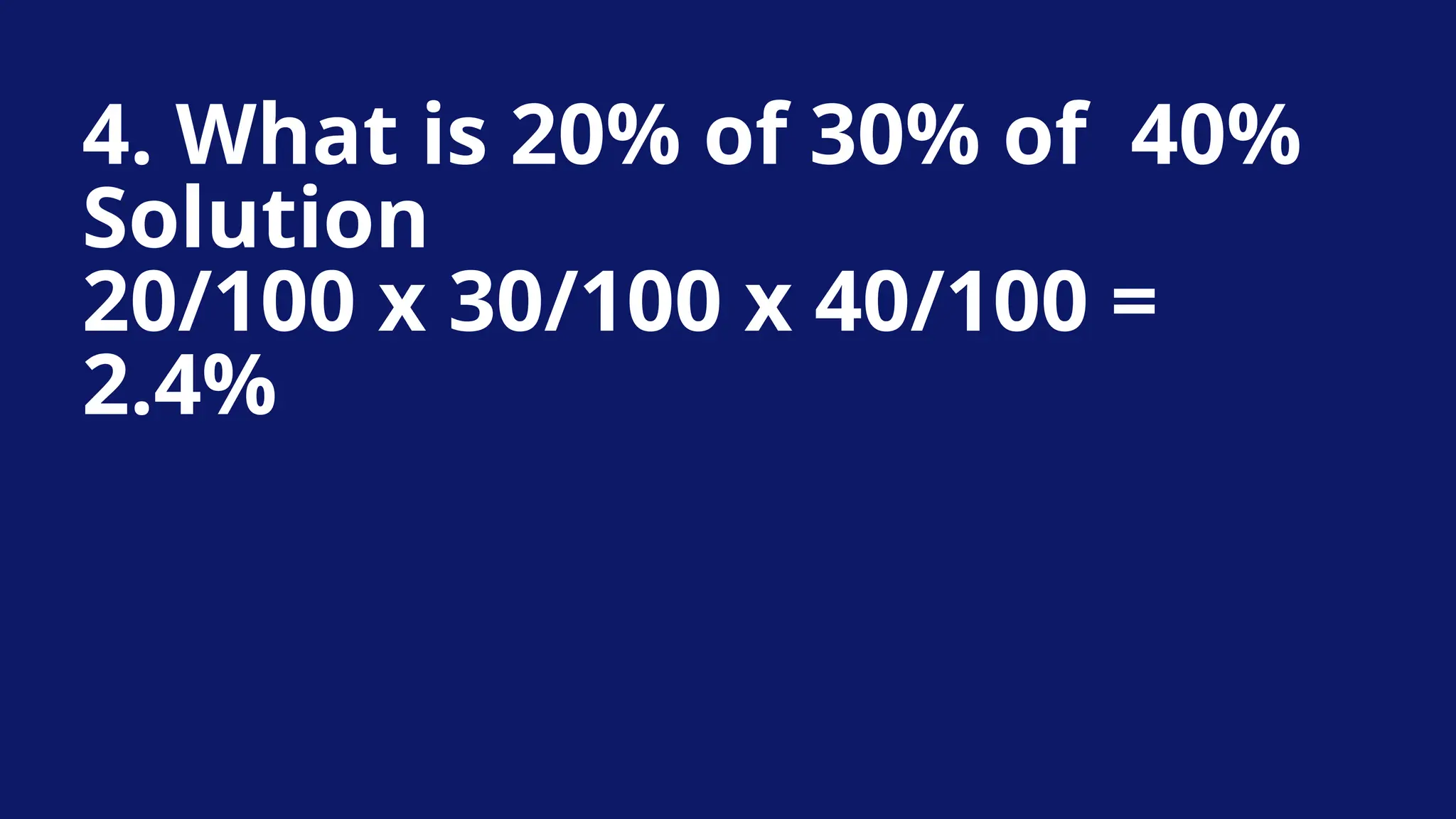























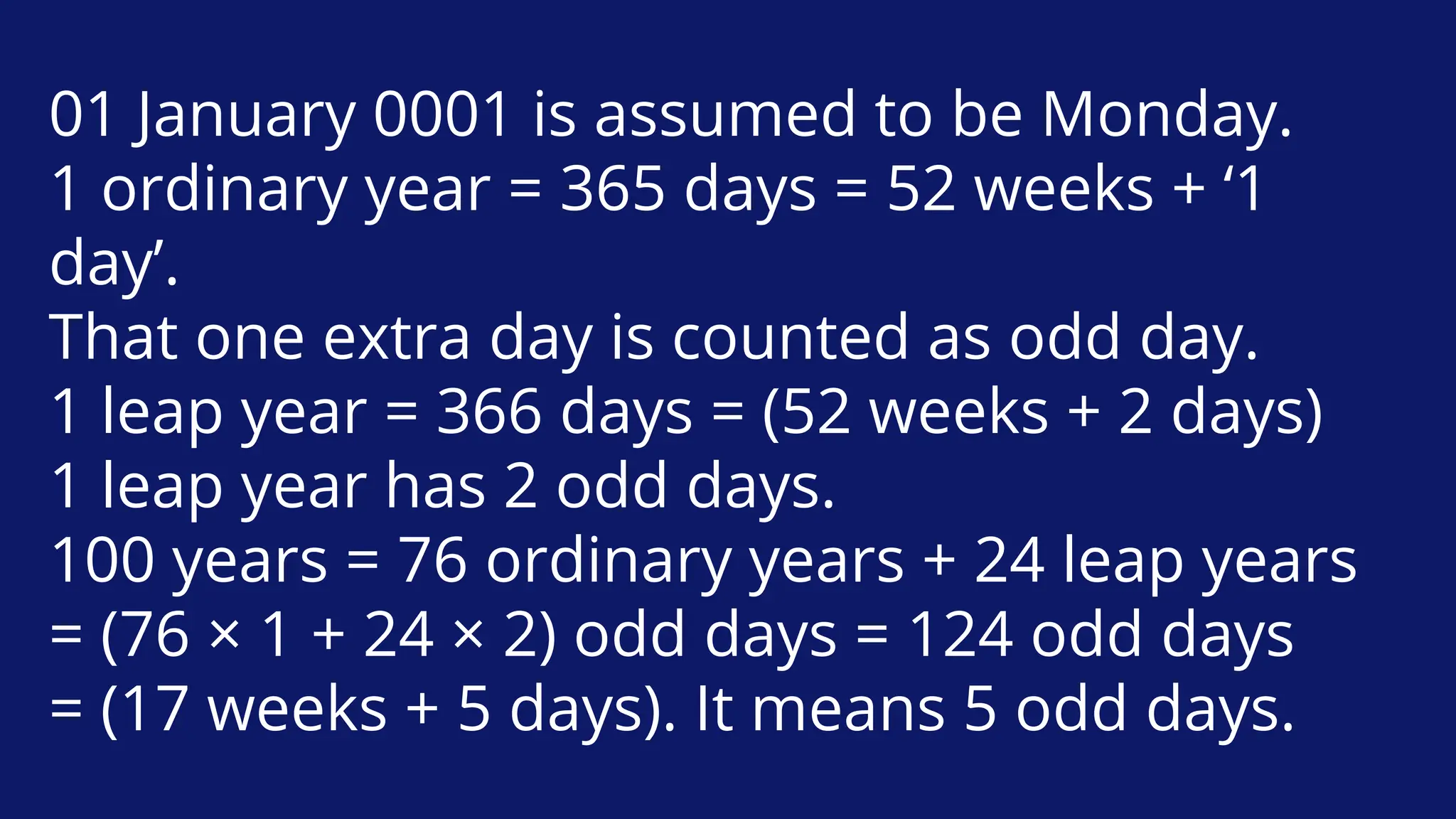
![Example
What was the day of the week on January 1, 2001?
[June 2009]
(a) Friday (b) Tuesday
(c) Sunday (d) Wednesday
Answer: (b)
Explanation
By the end of centuries 400, 800, 1200, 1600, 2000, 2400,
and so on, there are no extra days left. It means that the
last year 2000 was Sunday. As per convention, the week
starts with Monday and hence, the next day after last
day of year 2000, i.e., January 1, 2001, is Monday.](https://image.slidesharecdn.com/mathematicalreasoningaptitude-240505142250-cb2c6b1b/75/UGC-NET-Paper-1-Mathematical-Reasoning-Aptitude-pdf-122-2048.jpg)
![Example
January 1, 1995 was a Sunday. What would be the day of
the week on January 1, 1996? [December 2009]
(a) Sunday (b) Monday
(c) Wednesday (d) Saturday
Answer: (b)
Explanation
There is increase of 1 day (odd day) in the subsequent
year. In case of leap year (if the day is after February),
then there will be increase of two days.
Although 1996 is a leap year, the day in question is in
January month, so there will be increase of one day. Thus,
January 1, 1996 is Monday.](https://image.slidesharecdn.com/mathematicalreasoningaptitude-240505142250-cb2c6b1b/75/UGC-NET-Paper-1-Mathematical-Reasoning-Aptitude-pdf-123-2048.jpg)