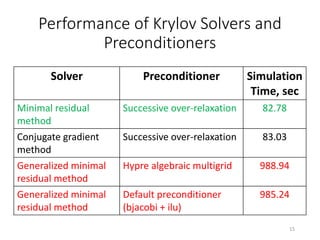
This document describes using the FEniCS framework to simulate electrical activity in the left ventricle of the heart in parallel. It implements the Ekaterinburg-Oxford model of cardiac electrophysiology on a 3D mesh of the left ventricle. Testing on a supercomputer showed near-linear scaling up to 240 CPU cores, reducing the simulation time from over 980 seconds to under 10 seconds. The choice of Krylov linear solver and preconditioner was found to significantly impact performance. The FEniCS implementation achieved similar performance as a previous manual implementation in C using OpenMP, but with better scalability.

1. Parallel Left Ventricle Simulation
Using the
FEniCS Framework
Timofei Epanchintsev and Vladimir Zverev
eti@imm.uran.ru
2nd Ural Workshop on Parallel, Distributed, and Cloud Computing for
Young Scientists

2. Anatomy of the Heart
2
L. Sherwood, Human physiology : from cells to systems. Australia ; United Kingdom:
Thomson Brooks/Cole, 2004.

3. Heart Simulation
3
Tissue OrganCell
• Multiscale modeling
• Cell
• Tissue
• Organ
• Heart simulation requires a lot of time
• Parallel computing is needed

4. Heart Simulation Obstacles
• Difficult code development for HPC
environment and its maintenance
• porting complicated code requires long time (3-
5 years). Modern architecture can become
obsolete;
• adaptation for HPC architecture often leads to
significant changes of code. Difficult to change
the mathematical models and numerical
methods in the optimized program
4

5. Automated Scientific Computing
Frameworks
5
• Automated Scientific Computing Frameworks
• OpenFOAM
• OpenCMISS
• Chaste
• FEniCS
• Advantages
• Software development using high level tools
• Automatic parallelization
• Disadvantage
• Low performance
• Performance improvements
• Just-in-time compilers, high performance mathematical libraries, etc.

6. The FEniCS framework
6

7. 7
• Ekaterinburg-Oxford [1] model describes electrical, chemical, and mechanical
processes
𝑑𝑆
𝑑𝑡
= 𝑔(𝑉, 𝑆)
• 𝑉 is the electrical potential, 𝑆 is the vector of state variables (the
dimension is 30) that governs the ion currents
𝑑𝑉
𝑑𝑡
= 𝐷𝛻2
𝑉 + 𝐼𝑖𝑜𝑛𝑠(V, S)
• 𝐷 is the diffusion matrix, 𝛻2 is the Laplace operator, and 𝐼𝑖𝑜𝑛𝑠 is the sum of the
ionic currents
1. Solovyova, O., Vikulova, N., Katsnelson, L.B., Markhasin, V.S., Noble, P., Garny, A., Kohl, P.,
Noble, D.: Mechanical interaction of heterogeneous cardiac muscle segments in silico: effects on Ca
2+ handling and action potential. International Journal of Bifurcation and Chaos 13(12) (2003)
Model of the Heart Electrical
Activity

8. Electric Potential and Ionic
Currents
8

9. Benchmark Problem
3D asymmetric left
ventricle model [1]
• Parameters were
captured by ultrasound
Implementation
• Operator splitting scheme
of the first order [2];
• Implicit method usage;
• No Newton-like iterations.
9
1. Pravdin, S.F., Berdyshev, V.I., Panfilov, A.V., Katsnelson, L.B., Solovyova, O., Markhasin, V.S.: Mathematical
model of the anatomy and fibre orientation field of the left ventricle of the heart. Biomedical engineering
online 54(12) (2013)
2. Li, Y., Chen, C.: An efficient split-operator scheme for 2-D advection-diffusion simulations using finite
elements and characteristics. Applied Mathematical Modelling 13(4) (1989) 248–253

10. FEniCS Program Example
# Formulation of the diffusion PDE variational problem
mesh = Mesh()
# Code for loading mesh from the file
# Building function space for action potential
Space_AP = FunctionSpace(mesh, "Lagrange", lagrange_order)
# Define the PDE Problem
v = TrialFunction(Space_AP)
v0 = Function(Space_AP)
PdePart = (1.0/dt)*inner(v - v0, q1)*dx
- (-inner(D*grad(v), grad(q1)))*dx
PDEproblem = LinearVariationalProblem(lhs(PdePart),
rhs(PdePart), v, bcs=bcs)
# Creating the PDE solver
PDEsolver = LinearVariationalSolver(PDEproblem)
10

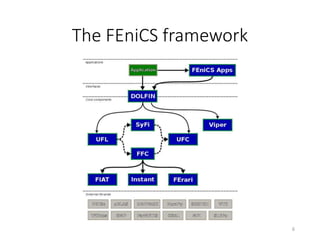
11. FEniCS Program Example
# Solving the differential equation systems
for t in time_range[1:]:
# Solving diffusion equation
assign(v0, v)
PDEsolver.solve()
# Solving cell equations
assign(ode_vars0, ode_vars)
assign(ode_vars0.sub(0), v)
ODEsolver.solve()
# Storing data if necessary
if steps % saving_step_interval == 0:
v_file << (v, t)
steps += 1
11

12. Krylov Solvers and
Preconditioners in FEniCS
12
Solver Preconditioner
Biconjugate gradient stabilized method Algebraic multigrid
Conjugate gradient method Default preconditioner (bjacobi + ilu)
Generalized minimal residual method Hypre parallel incomplete LU
factorization
Minimal residual method Hypre parallel sparse approximate
inverse
Richardson method Incomplete Cholesky factorization
Transpose-free quasi-minimal residual
method
Incomplete LU factorization
Hypre algebraic multigrid
Successive over-relaxation

13. Computational Experiment
• Supercomputer “URAN”
• CPU - 2 x Intel(R) Xeon(R) CPU X5675 @ 3.07GHz
• RAM - 192 GB
• Interconnect - Infiniband DDR (20 Gbit)
• OS - Red Hat Enterprise Linux 6.7
• FEniCS version 1.6.0
13

14. Computational Experiment
• Mesh generated by GMSH
• size of tetrahedron is 2-4mm;
• mesh contains 7178 points and 26156 tetrahedrons.
• Initial conditions
• activation of an entire LV (action potential = 40 mV)
• Time step 2.5e-5 seconds
• in order to capture fast processes.
• The simulation period 0.3 seconds
• electrical activity tends to the equilibrium state.
14

15. Performance of Krylov Solvers and
Preconditioners
15
Solver Preconditioner Simulation
Time, sec
Minimal residual
method
Successive over-relaxation 82.78
Conjugate gradient
method
Successive over-relaxation 83.03
Generalized minimal
residual method
Hypre algebraic multigrid 988.94
Generalized minimal
residual method
Default preconditioner
(bjacobi + ilu)
985.24

16. The Simulation Time
16
Minimal residual method solver,
Successive over-relaxation preconditioner

17. Simulation Speedup
17
Minimal residual method solver,
Successive over-relaxation preconditioner

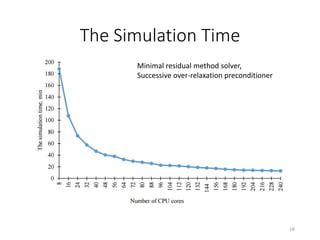
18. Comparison with manual
implementation
LeVen
• Our previous implementation [1]
• C language
• OpenMP for shared memory
systems
• Limited scalability
Comparison with LeVen
• Same performance
• Better scalability
18
1. Sozykin, A., Pravdin, S., Koshelev, A., Zverev, V., Ushenin, K., Solovyova,
O.: LeVen - a parallel system for simulation of the heart left ventricle. 9th
IEEE International Conference on Application of Information and
Communication Technologies, AICT 2015 Proceedings (2015) 249–252

19. Conclusion
FEniCS framework is an efficient tool for heart simulation on parallel
computing systems
• Near-mathematical notation
• Automatic parallelization on MPI clusters
Performance testing case
• Simulation of heart electrical activity using Ekaterinburg-Oxford model
• Approximately the same performance as the implementation using the
C programming language
• 90x speedup using the 240 CPU cores
• Near-linear scalability
• The type of Krylov linear solver and preconditioner significantly
influence the simulation time
19

20. Thank you for your attention!
Epanchintsev Timofei
• eti@imm.uran.ru
Parallel Left Ventricle
Simulation Using the
FEniCS Framework
This work was supported by the Russian Science Foundation (grant no.
14-35-00005). Our study was performed using the Uran
supercomputer of the Krasovskii Institute of Mathematics and
Mechanics.
20

21. 21