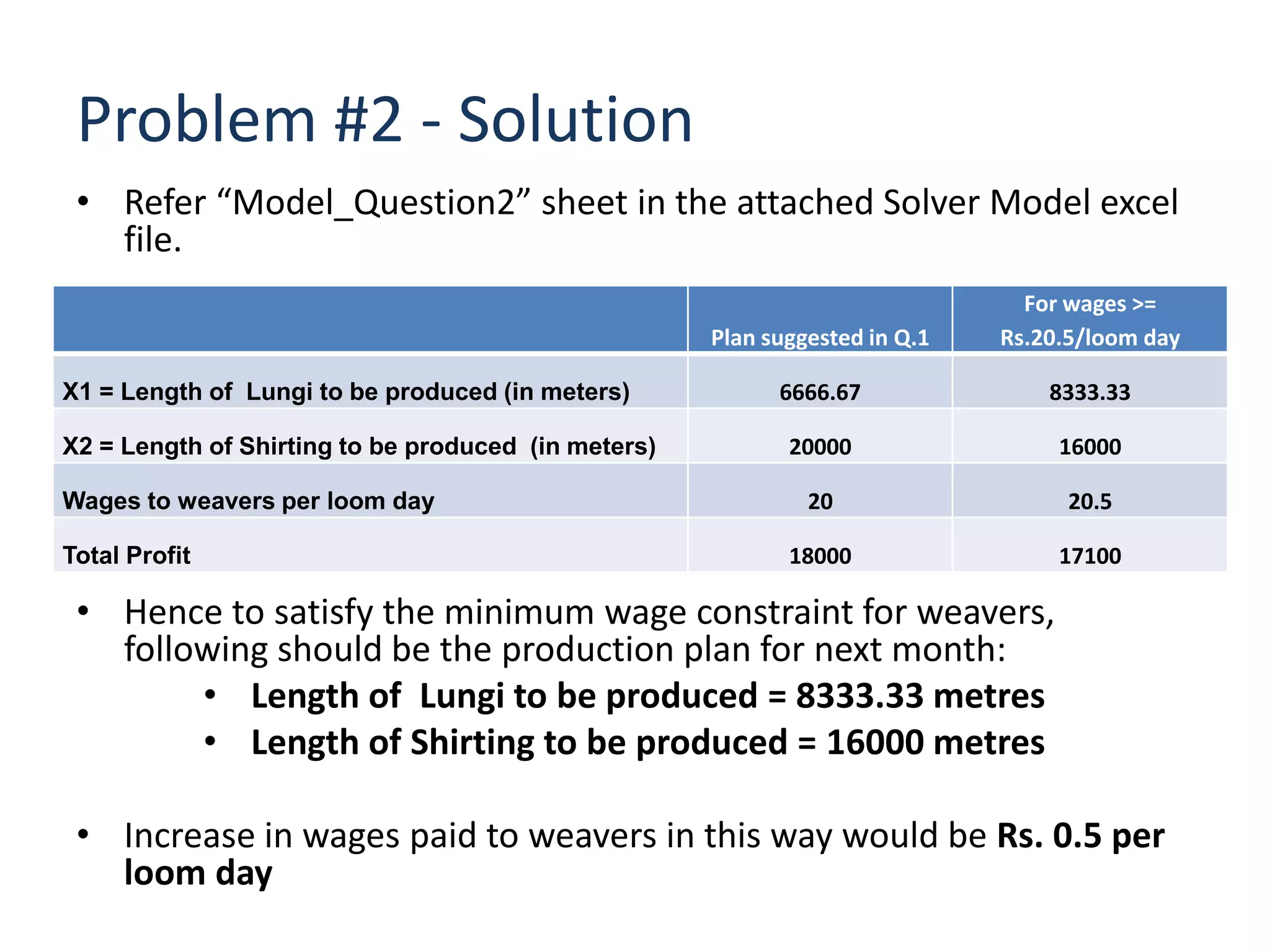
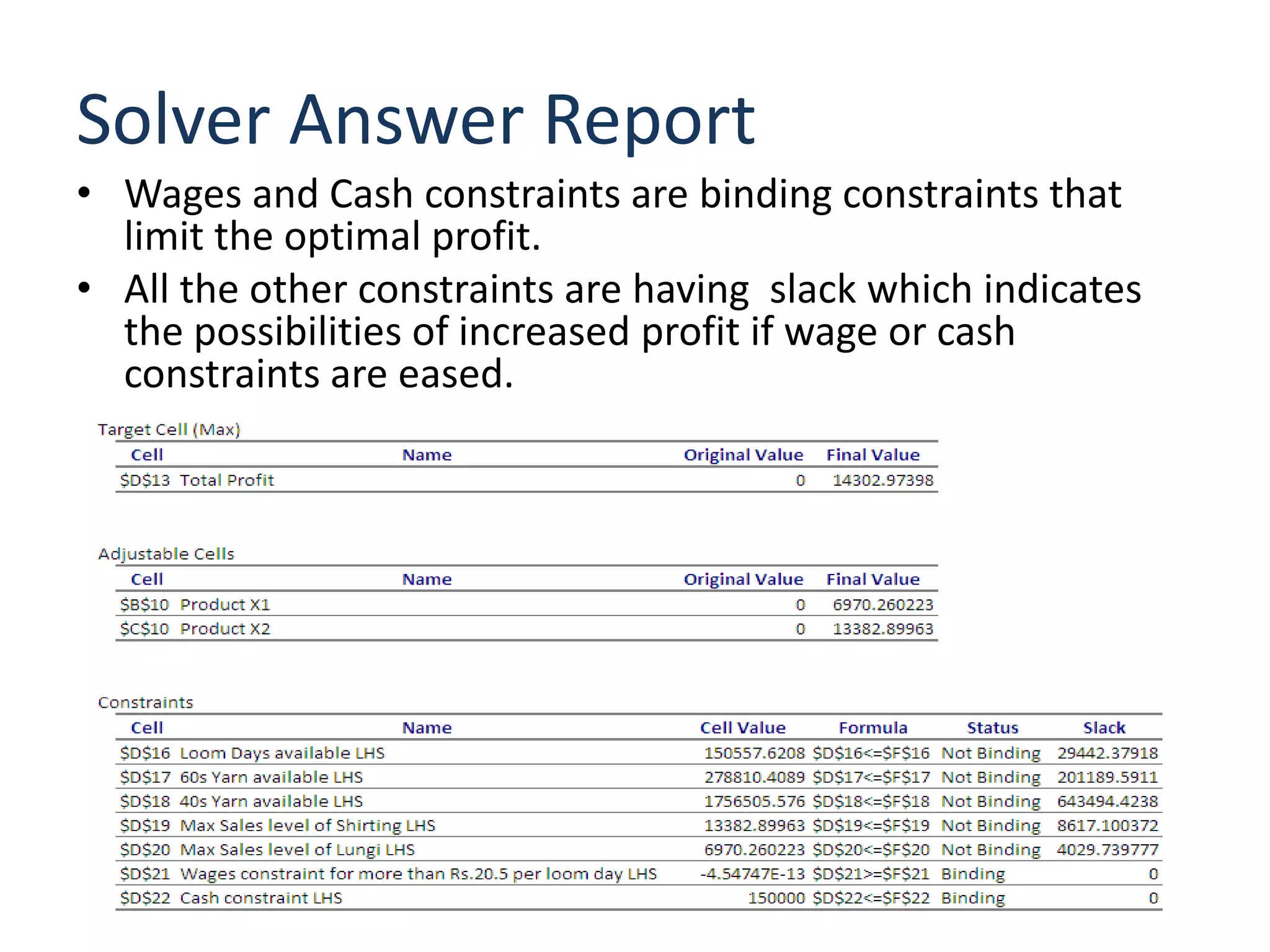
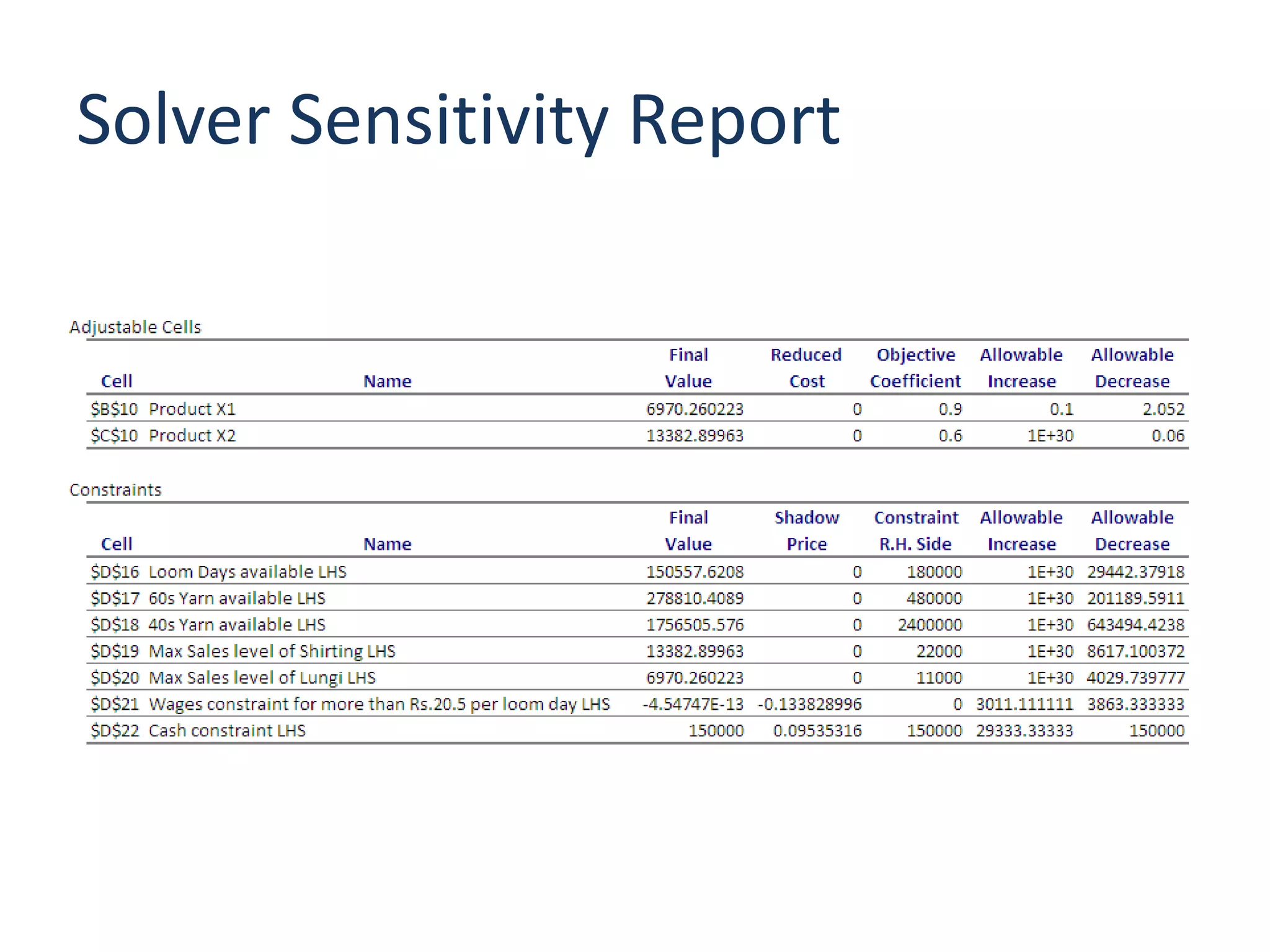
The document discusses optimizing the product mix at Panchtantra Corporation to maximize profit under various constraints. Mr. Ganesh must determine how many meters of Lungi and Shirting to produce. The objective is to maximize total sales profit. Constraints include loom days, yarn availability, sales limits, wages paid to weavers, and cash available. The optimal solution is found to be 6,970 meters of Lungi and 13,383 meters of Shirting given the cash constraint of Rs. 150,000. Wages and cash constraints limit the optimal profit while other constraints have slack.

1. Operation Research Project Work
Topic: Planning the Product Mix at
Panchtantra Corporation

2. Introduction
• Mr. Ganesh had to prepare a production plan of
Intensive Handloom Development project for the next
month.
• Types of handloom to be produced :
• Lungi (60sx40s)
• Shirting (40sx40s)
• The main objective of Mr. Ganesh was to decide over
how many metres of Lungi and shirting should be
produced in order to maximize the profit satisfying the
various constraints.

3. Exihibit 1
S. No. Parameter Lungi Shirting
1 Selling Price (Rs. Per metre) 10.9 6.6
2 Variable Cost
2.a. Wages paid to weavers (Rs. Per metre) 4.5 1.5
2.b. Yarn Cost (Rs. Per metre) 5.5 4.5
3 Contribution (Rs. Per metre) 0.9 0.6
4 Production Rate (No. of metre per loom day) 5 12
5 Yarn Consumption (grams per metre)
5.a. 40s yarn 60 100
5.b. 60s yarn 40 0

4. Decision Variables
• Mr. Ganesh had to decide over the product
Mix i.e. how many metres of Lungi and
Shirting should be produced.
Therefore Decision Variable are :
Length of Lungi to be produced (in metres) = X1
Length of Shirting to be produced (in metres) = X2

5. Objective Function
• Maximizing the Total Sales Profit
Profit per metre of Lungi = Rs. 0.9
Profit per metre of Shirting = Rs. 0.6
Therefore, Objective Function is :
Max (0.9 X1 + 0.6 X2)

6. Constraints
• Various constraints that affect the production and
the decision variables are listed in following slides
1. Maximum number of Loom Days available are 3000
Loom Days <= 3000
» (X1/5)+(X2/12) <= 3000
» 12X1 + 5X2 <= 3000 x 60
» 12X1 + 5X2 <= 180000 --(1)

7. Constraints (contd.)
2. 60s Yarn available was 480 Kgs.
60s yarn <= 480 kgs.
60s yarn is used only for Lungi at the rate of 40 grams per
metre.
» 40X1 <= 480x1000 --(2)
3. 40s Yarn available was 2400 Kgs.
40s yarn <= 2400 kgs.
40s yarn is used in Lungi at the rate of 60 grams per metre
and in Shirting at the rate of 100 grams per metre
» 60X1 + 100X2 <= 240x1000 --(3)

8. Constraints (contd.)
4. As per sales department, due to piled up stocks in
inventory, production of Shirting should not be more
than 22000 metres.
Sales level of Shirting <= 22000 metres
» X2 <= 22000 --(4)
5. As per sales department, due to piled up stocks in
inventory, production of Lungi should not be more
than 11000 metres.
Sales level of Lungi <= 11000 metres
» X1 <= 11000 --(5)

9. Problem #1 - Analysis
• Mr. Ganesh wanted to produce as much of lungi
as possible, therefore he would want to use the
entire sales limit of 11000 mts.
Therefore, the constraint #5 would be as :
X1 = 11000 --(5.a)
• Mr. Ganphathy was however in favor of
producing only the optimal level of Lungi so that
the rest of the resources can be used for
maximizing the profit.
Therefore, the constraint #5 would be as :
X1 <= 11000 --(5.b)

10. Problem #1 - Solution
• Refer “Model_Question1” sheet in the attached Solver Model excel
file.
As per Mr. Ganesh's As per Mr.
plan Ganphathy's plan
X1 = Length of Lungi to be produced (in metres) 11000 6666.67
X2 = Length of Shirting to be produced (in metres) 9600 20000
Total Profit 15660 18000
• Hence To optimize the profit, following should be the production
plan for the next month (we should go with Mr. Ganphaty's Plan):
• Length of Lungi to be produced = 6666.67 metres
• Length of Shirting to be produced = 20000 metres
• Increase in profit in this way will be Rs. 2340 with optimal profit of
Rs. 18000

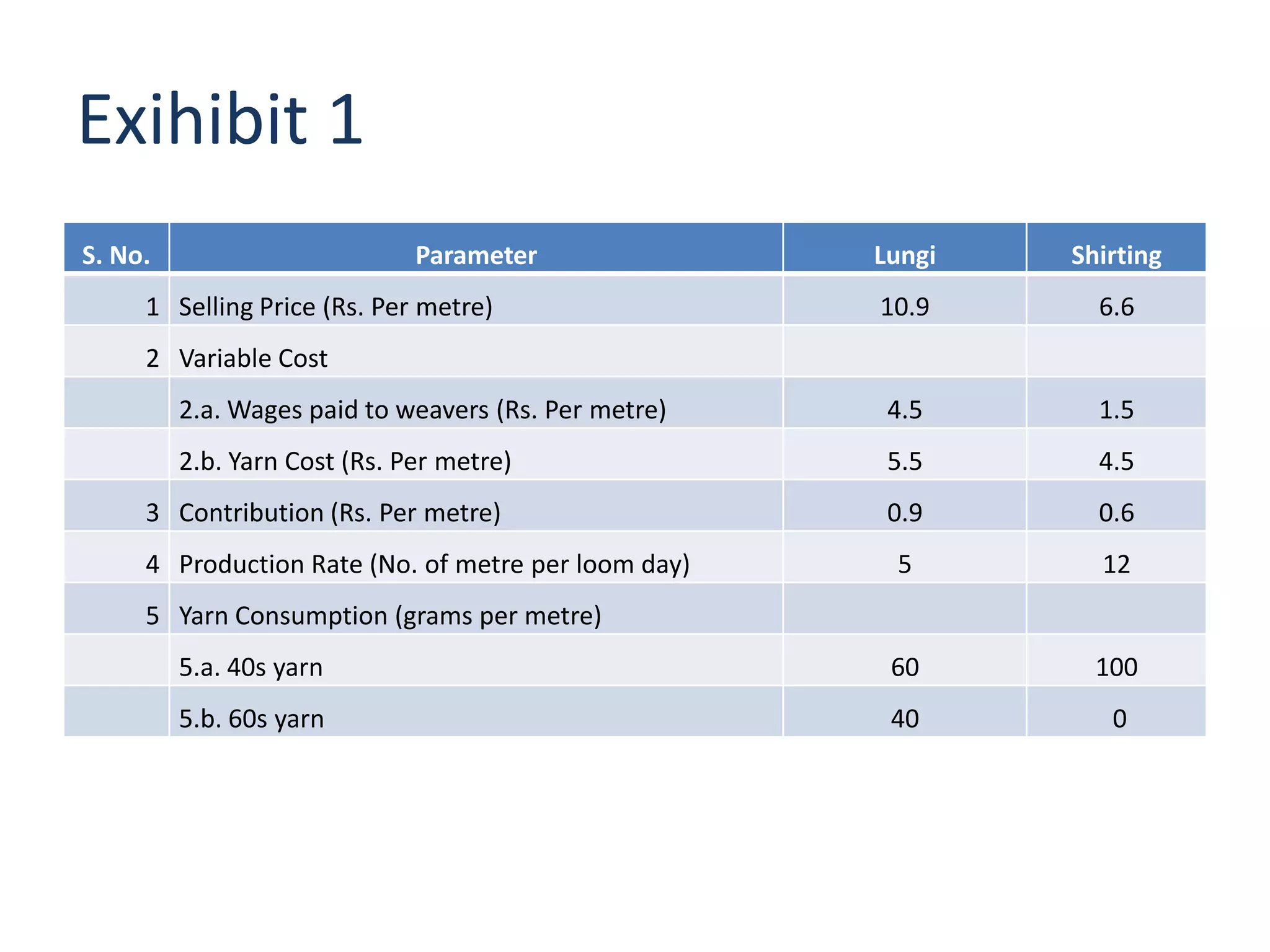
11. Problem #2 – Additional Constraint
• Additional constraint added to ensure that on an
average, the production paid as wages to the weavers at
least Rs. 20.5 per loom day.
• Total wages for the production could be given by
4.5X1 + 1.5X2
• Total number of loom days used could be given by
(X1/5) + (X2/12)
• Therefore
4.5X1 + 1.5X2 >= 20.5 x [(X1/5) + (X2/12)]
» (4.5-20.5/5)X1 + (1.5 - 20.5/12)X2 >= 0
» 0.4X1 – 0.2083X2 >= 0 -- (6)

12. Problem #2 - Solution
• Refer “Model_Question2” sheet in the attached Solver Model excel
file.
For wages >=
Plan suggested in Q.1 Rs.20.5/loom day
X1 = Length of Lungi to be produced (in meters) 6666.67 8333.33
X2 = Length of Shirting to be produced (in meters) 20000 16000
Wages to weavers per loom day 20 20.5
Total Profit 18000 17100
• Hence to satisfy the minimum wage constraint for weavers,
following should be the production plan for next month:
• Length of Lungi to be produced = 8333.33 metres
• Length of Shirting to be produced = 16000 metres
• Increase in wages paid to weavers in this way would be Rs. 0.5 per
loom day

13. Problem #3 – Additional Constraint
• As informed by Finance Manager, Cash
available with Panchtantra Corporation is Rs.
1.50 Lakhs
• Variable (Wages and Yarn cost) were paid in
cash. Therefore, total variable cost during
production will be :
(4.5+5.5)X1 + (1.5+4.5)X2
• Hence, the additional constraint :
(4.5+5.5)X1 + (1.5+4.5)X2 <= 150000 --(7)

14. Problem #3 – Solution
• Refer “Model_Question3” sheet in the attached
Solver Model excel file.
• Hence, by taking the cash constraint into the
consideration, following should be the production
plan for next month:
X1 = Length of Lungi to be produced (in metres) 6970.26
X2 = Length of Shirting to be produced (in metres) 13382.90
Optimal Profit 14302.97

15. Solver Answer Report
• Wages and Cash constraints are binding constraints that
limit the optimal profit.
• All the other constraints are having slack which indicates
the possibilities of increased profit if wage or cash
constraints are eased.

16. Solver Sensitivity Report

17. End of slides