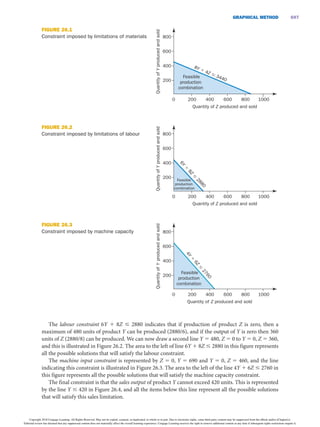
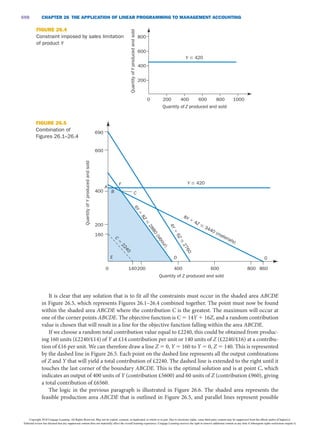
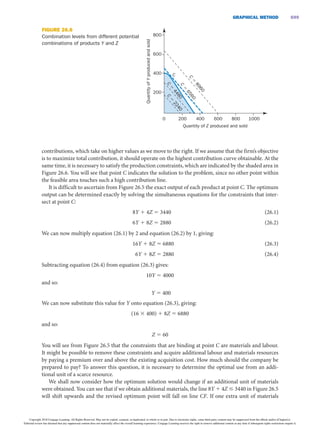
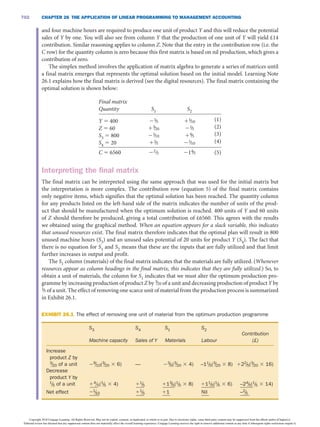
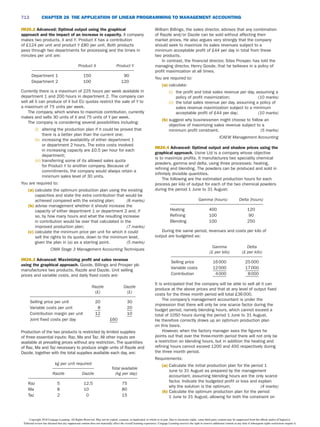
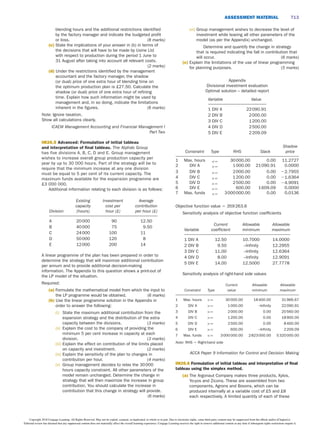
This document discusses using linear programming techniques to determine the optimal production program when more than one scarce resource exists. It presents an example problem involving a company that produces two products with limitations on labor hours, materials, and machine capacity. The document formulates the linear programming model to maximize total contribution subject to the resource constraints. It describes using the graphical method to visualize and solve the problem when only two products are involved, finding the optimal output levels that satisfy all constraints.