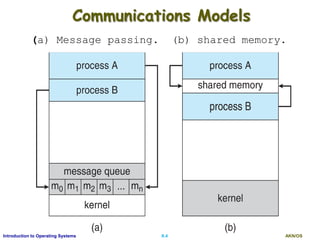
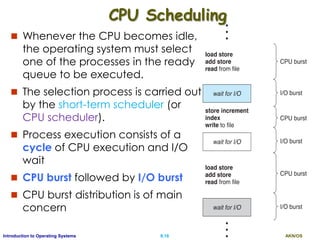
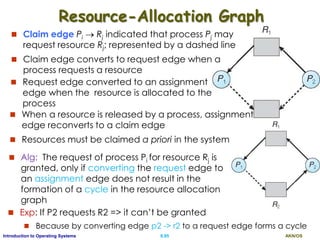
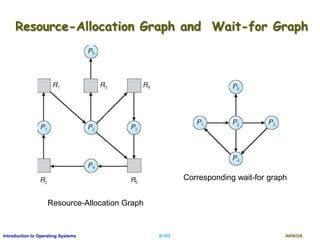
This document discusses interprocess communication and CPU scheduling in operating systems. It covers two models of interprocess communication: shared memory and message passing. It also describes different CPU scheduling algorithms like first-come first-served (FCFS), shortest job first (SJF), priority scheduling, and round-robin. The key aspects of process synchronization, producer-consumer problem, and implementation of message passing are explained.





















![AKN/OSII.24Introduction to Operating Systems
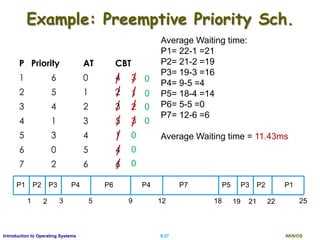
SJF Contd.
SJF can either be preemptive or non- preemptive
Preemptive SJF is known as shortest-remaining-time-first
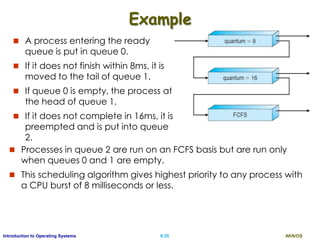
Example
Proc. A.Time Burst
P1 0 8
P2 1 4
P3 2 9
P4 3 5
P1 P2 P4 P3
0 8 12 17 26
Non-preemptive
P4
0 1 26
P1
P2
10
P3
P1
5 17
Preemptive
Average waiting time for non-preemptive SJF?
[(0-0)+(8-1)+(12-3)+(17-2) ]/ 4 = 7.75ms
Average Waiting time for preemptive SJF?
[(0-0)+(1-1)+(5-3) +(10-1) +(17-2)]/4 = 6.5 ms](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-24-320.jpg)
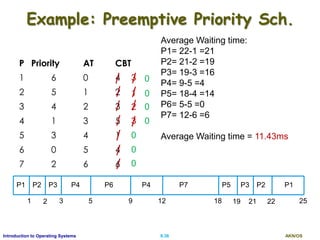
![AKN/OSII.25Introduction to Operating Systems
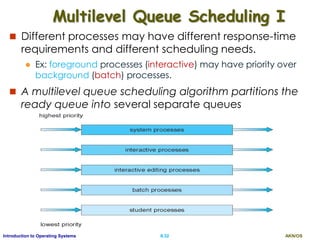
Priority Scheduling
A priority is associated with each process, and the CPU
is allocated to the process with the highest priority.
Equal-priority processes are scheduled in FCFS order.
An SJF algorithm is simply a priority algorithm where the
priority (p) is the inverse of the (predicted) next CPU
burst.
The larger the CPU burst, the lower the priority, and vice versa.
Example (lowest integer is highest priority)
Proc. Burst Priority
P1 10 3
P2 1 1
P3 2 4
P4 1 5
P5 5 2
Average Waiting time?
[0+1+6+16+18]/5 = 8.2 ms
P2 P5 P1 P3 P4
0 1 196 16 18](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-25-320.jpg)



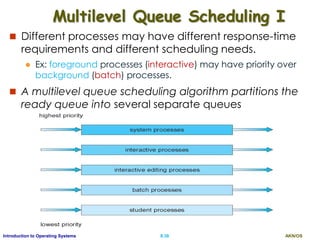
![AKN/OSII.30Introduction to Operating Systems
Round-Robin Example with TQ=4
Process Burst
P1 24
P2 3
P3 3
P P P1 1 1
0 18 3026144 7 10 22
P2
P3
P1
P1
P1
Average waiting time?
[(10-4) + 4+ 7]/3 = 5.67ms
If there are n processes in the ready queue and the time quantum is
q, then each process gets 1/n of the CPU time in chunks of at most q
time units.
Each process must wait no longer than (n - 1) x q time units until its
next time quantum.
Example: Five processes and a time quantum of 20ms.
i.e. each process will get up to 20 milliseconds in every 100ms.](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-30-320.jpg)







![AKN/OSII.43Introduction to Operating Systems
Producer
while (true) {
/* produce an item in next_produced*/
while (counter == BUFFER_SIZE) ;
/* do nothing */
buffer[in] = next_produced;
in = (in + 1) % BUFFER_SIZE;
counter++;
} while (true) {
while (counter == 0) ;
/* do nothing */
next_consumed = buffer[out];
out = (out + 1) % BUFFER_SIZE;
counter--;
/* consume the item in next_consumed*/
}
Consumer](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-43-320.jpg)






















![AKN/OSII.66Introduction to Operating Systems
Dining-Philosophers Problem
It is a simple representation of allocating several resources among
several processes in a deadlock-free and starvation-free manner.
represent each chopstick with a semaphore.
Semaphore chopstick [5]
All elements are initialized to 1
Philosophers spend their lives alternating
thinking and eating
Don’t interact with their colleagues, when
hungry, try to pick up 2 chopsticks (one at a
time) that are closest to her
When a hungry philosopher has both her
chopsticks at the same time, she eats.
When she is finished eating, she puts
down both of her chopsticks and starts
thinking again.](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-66-320.jpg)
![AKN/OSII.67Introduction to Operating Systems
The structure of Philosopher i
do {
wait (chopstick[i] );
wait (chopStick[ (i + 1) % 5] );
// eat
signal (chopstick[i] );
signal (chopstick[ (i + 1) % 5] );
// think
} while (TRUE);
Solution guarantees that no two neighbors are eating
simultaneously
But may result in a deadlock
If all five philosophers become hungry simultaneously and each
grabs her left chopstick.
All the elements of chopstick will now be equal to 0. When they
try to grab their right chopstick, they will be delayed forever.](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-67-320.jpg)







![AKN/OSII.76Introduction to Operating Systems
Monitor Solution to Dining Philosophers
monitor DiningPhilosophers {
enum { THINKING; HUNGRY, EATING) state [5] ;
condition self [5];
void pickup (int i) {
state[i] = HUNGRY;
test(i); //makes eating if two chopsticks found
if (state[i] != EATING) self[i].wait;
}
void putdown (int i) {
state[i] = THINKING;
// test left and right neighbors
test((i + 4) % 5);
test((i + 1) % 5);
}](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-76-320.jpg)
![AKN/OSII.77Introduction to Operating Systems
Solution to Dining Philosophers (Cont.)
void test (int i) {
if ((state[(i + 4) % 5] != EATING) &&
(state[i] == HUNGRY) &&
(state[(i + 1) % 5] != EATING) ) {
state[i] = EATING ;
self[i].signal () ;
}
}
initializationCode() {
for (int i = 0; i < 5; i++)
state[i] = THINKING;
}
}](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-77-320.jpg)















![AKN/OSII.97Introduction to Operating Systems
Data Structures for the Banker’s Algorithm
Let n = # of processes, and m = # of resource types
Available: Vector of length m.
If available [ J ] = k, there are k instances of resource type RJ
available
Max: n x m matrix.
If Max [ i, J ] = k, then process Pi may request at most k
instances of resource type RJ
Allocation: n x m matrix.
If Allocation[ i, J ] = k, then Pi is allocated with k instances of RJ
Need: n x m matrix.
If Need[i, J] = k, then Pi may need k more instances of RJ to
complete its task
Need [ i, J ] = Max[ i, J ] – Allocation [ i, J]](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-97-320.jpg)
![AKN/OSII.98Introduction to Operating Systems
Banker’s Safety Algorithm
1. Let Work and Finish be vectors of length m and n,
respectively. Initialize:
Work = Available
Finish [ i ] = false for i = 0, 1, …, n- 1
2. Find an i such that both:
(a) Finish [ i ] = false
(b) Needi Work
If no such i exists, go to step 4
3. Work = Work + Allocationi
Finish[i] = true
go to step 2
4. If Finish [i] == true for all i, then the system is in a safe
state](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-98-320.jpg)
![AKN/OSII.99Introduction to Operating Systems
Resource-Request Algorithm for Process Pi
Requesti = request vector for Pi.
Requesti [ J ] = k , Pi wants k instances of RJ
Algorithm
1. If Requesti Needi go to step 2.
a) Otherwise, raise error, since it has exceeded its maximum claim
2. If Requesti Available, go to step 3.
a) Otherwise Pi must wait, since resource not available
3. Pretend to allocate requested resources to Pi by modifying
the state as follows:
a) Available = Available – Requesti;
b) Allocationi = Allocationi + Requesti;
c) Needi = Needi – Requesti;
4. If safe the resources are allocated to Pi
a) Otherwise Pi must wait, and the old resource-allocation state is
restored](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-99-320.jpg)

![AKN/OSII.101Introduction to Operating Systems
P1 Request (1,0,2)
Check that Request Available (that is, (1,0,2) (3,3,2) true
So find the new state at time T1
Allocation Need Available
A B C A B C A B C
P0 0 1 0 7 4 3 2 3 0
P1 3 0 2 0 2 0
P2 3 0 2 6 0 0
P3 2 1 1 0 1 1
P4 0 0 2 4 3 1
Now execute safety algorithm and find the safe sequence
1. Work = Available, Finish [ i ] = false for i = 0, 1, 2, 3, 4
2. Find an i such that
Finish [ i ] = false & Needi Work
If no such i exists, go to step 4
3. Work = Work + Allocationi
Finish[i] = true, go to step 2
4. If Finish [i] == true for all i, is in a safe state
Safe sequence is < P1, P3, P4, P0, P2>, so request allowed.
Can request for (3,3,0) by P4 be granted? At T0, if yes then find the
safety sequence
Can request for (0,2,0) by P0 be granted? At T0 , if yes then find
the safety sequence](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-101-320.jpg)

![AKN/OSII.104Introduction to Operating Systems
Several Instances of a Resource Type
Available:
A vector of length m => the number of available
resources instances
Allocation:
An n x m matrix => the number of resources
instances of each type currently allocated.
Request:
An n x m matrix => the current request of each
process.
If Request [i][J] = k, then process Pi is requesting k
more instances of resource type RJ.](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-104-320.jpg)
![AKN/OSII.105Introduction to Operating Systems
Detection Algorithm
1. Let Work and Finish be vectors of length m and n, initialized as
follows
(a) Work = Available
(b) For i = 1,2, …, n, if Allocationi 0, then
Finish[i] = false; otherwise, Finish[i] = true
2. Find an index i such that:
(a) Finish[i] == false
(b) Requesti Work
If no such i exists, go to step 4
3. Work = Work + Allocationi
Finish[i] = true
go to step 2
4. If Finish[i] == false, for some i, 1 i n, then the system is in
deadlock state.
Moreover, if Finish[i] == false, then Pi is deadlocked
Algorithm requires an order of
O(m x n2) operations to detect
a deadlocked state](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-105-320.jpg)
![AKN/OSII.106Introduction to Operating Systems
Example of Detection Algorithm
Five processes P0 through P4; three resource types
A (7 instances), B (2 instances), and C (6 instances)
Snapshot at time T0:
Allocation Request Available
A B C A B C A B C
P0 0 1 0 0 0 0 0 0 0
P1 2 0 0 2 0 2
P2 3 0 3 0 0 0
P3 2 1 1 1 0 0
P4 0 0 2 0 0 2
Find if there is a deadlock?, if no then find the sequence.
Sequence <P0, P2, P3, P1, P4> will result in Finish[i] = true for all i
Suppose P2 requests an additional instance of type C, then find the
system status
i.e. No deadlock => process execution sequence
Deadlock => list of deadlocked process](https://image.slidesharecdn.com/ospartii-170526070622/85/Operating-Systems-Part-II-Process-Scheduling-Synchronisation-Deadlock-106-320.jpg)


