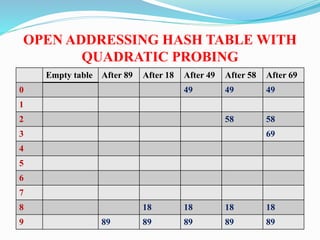
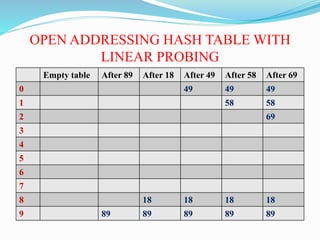
The document discusses different techniques for handling collisions in hash tables, including separate chaining and open addressing. Separate chaining uses linked lists to chain together elements that hash to the same slot, while open addressing resolves collisions by probing to alternate slots using functions like linear probing, quadratic probing, and double hashing. Pseudocode is provided for initializing and inserting elements into a hash table using separate chaining with linked lists.

1. HASHING
(Separate chaining, Closed Hashing)
K.HARIPRITHA.
M.Sc(Info Tech).
Nadar Saraswathi college of arts and science.

2. Synopsis:
 SEPARATE CHAINING
 Open Hashtable.
 Type declaration for separate chaining.
 Insert routine for separate chaining Hash
Table
 Initialization routine for separate chaining
Hash table.
OPEN ADDRESSING
Linear Probing
Quadric Probing
Double Hashing

3. SEPARATE CHANNING
(Open hashing)
 Open hashing is to keep a list of all elements that hash to
the same value.
 In the space is tight , it might be preferable to avoid their
use.
 In this section that the keys are the first 10 perfect squares
and that the hash function is simply Hash(X)=X mod 10.
 That we use the hash function to determine which list to
traverse this list in the normal manner , returning the
position where the item is found.

4. OPEN HASH TABLE

5.  To be involve insert. we travese down the appropriate list to
check then the element is placed.
 If the element turns out to be new it is inserted either at the
front of the list or at the end of the list.
 This is easily addressed while the code is being written.In the
new element are sometimes are inserted at thre front of the list.The class
specification required to implement the open hashing.
 Last item is accessed by the accessing item in the current list
with the ()operator.
 The lists are automatically initialized by the list constructor.
 Routines to copy and reinitialize are provided. Line 4 through 6 allocate a
hash table structure.
 H will be point to s structure containing an integer and a pointer to a
list.Line 7 sets table size to a prime number and lines 8 through 10 attempt to
allocate an array of list.
 Implementation uses header allocate one header per list and set its next field
to NULL.

6. Type declaration for separate chaining
hash table
#ifndef_hashsep_H
Struct ListNode;
Typedef struct ListNode *Position;
Struct HashTbl;
typedef struct HashTbl *Hash Table;
HashTable Initialize (int Tablesize);
Void DestroyTable (HashTable H);
Position Find (ElementType Key,
HashTable);
Void insert(ElementType key, HashTable
H);
Element type retrive(position p);
/*Routines such as Delete and make
empty are omitted */
#endif /*_Hashsep_H*/
/* Place in the implementation file*/
struct ListNode
{
ElementType Element;
Position Next;
};
Typedef Position Lists;
/*List *The List will be an array of
lists,allocated later
/*The lists use header (for simplicity,*),*/
/*though this wastes space*/
Struct HashTb
{
int TableSize;
Lists*TheLists;
};

7. Insert routine for separate chaining Hash table
Void
Insert(ElementType key,HashTable H)
{
Position pos,Newcell;
List L;
/*1*/ Pos=Find(key, H);
/*2*/if (pos==NULL)/*Key is not found*/
/*3*/Newcell=malloc(sizeof(struct ListNode));
/*4*/if(Newcell==NULL)
/*5*/ Fatalerror(“Out of space”);
else
{
/*6*/ L=H->The Lists[Hash(Key,H->TableSize)];
/*7*/Newcell->Next=L->Next;
/*8*/Newcell->Element=key; /*Probably need strcpy!*/
/*9*/L->Next =NewCell;
}
}
}

8. Initialization routine for separate
chaining hash table
HashTable
InitializeTable(int Tablesize)
{
HashTable H;
int I;
/*1*/ if (TableSize<MinTableSize)
{
/*2*/ Error (“table size too small”);
/*3*/ return NULL;
}
/*Allocate table*/
/*4*/H=malloc(sizeof(struct HashTbl));
/*5*/if(H==NULL)
/*6*/FatalError(“Out of space!!!”);
/*7*/H->Tablesize = Nextprime(TableSize)
/*Allocate arraay of list*/
/*8*/H->The lists =malloc (sizeof(List)*H-
>TableSize);
/*9*/if (H->TheLists==NULL)
/*10*/ FatalError(“Out of space!!!”);
/*Allocate list header*/
/*11*/ for (i=0;i<H->TableSize;i++)
{
/*12*/H->The Lists [i]=malloc(Sizeof(struct
ListNode));
/*13*/if (H->The lists[i]==NULL)
/*14*/FatalError(“Out of space!!!”);
else
/*15*/ H->The lists[i]->Next=NULL;
}
/*16*/ return H;
}

9.  The deletion routine is a straightforward implementation
of deletion in a linked list,so will not bother with it here.
 If the table is large and the hash function is good,all the
lists should be short so it is not worthwhile to try anything
cmplicated.
 The loaded factor ʎ of a hash table to the ratio of the
number element to the hash table to the table
size.(ex:above ʎ=1.0. The average length of the list is ʎ)
 The number of the link to traverse is ʎ on average.A
successful search requires that about 1+(ʎ+2)link be
traversed.
 The general rule for separate chaining hashing is to make
the table size about the large as the number of the element
expected

10. OPEN ADDRESSING
 Open addressing, or closed hashing, is a method
of collision resolution in hash tables.
Open addressing hashing is an alternative to resolving
collisions with linked list.
Separate chaining hashing has the disadvantage of using
linked lists.
The algorithm down a bit because of the time to allocate
new cells.
Its essentially requires the implements of a second data
structure.

11. Cells h0(x),h1(x),h2(x)... N.
F(0)=0 the function f, is the collision
resolution strategy.
The load factor ℷ=0.5
hi(x)=(hash(x)+f(i))

12. LINEAR PROBING
The amounts to trying cells sequentially in search of
empty cell.
The result of inserting keys {89,18,49,58,69} into a
hash table using the same hash function.
The collision resolution strategy ,f(i)=i.
The first collision occurs when 49 is inserted; in spot
0,which is open.
Unsuccessful search ½(1+1/(1-ℷ)2)
Successful search ½(1+1/(1-ℷ))

13. 0
1
2
3
4
5
6
7
8
9
 Linear Probing: after
checking spot h(k), try
spot h(k)+1, if that is full,
try h(k)+2, then h(k)+3,
etc.
Insert:
38
19
8
109
10

14. OPEN ADDRESSING HASH TABLE WITH
LINEAR PROBING
Empty table After 89 After 18 After 49 After 58 After 69
0 49 49 49
1 58 58
2 69
3
4
5
6
7
8 18 18 18 18
9 89 89 89 89 89

15. Quadratic Probing
f(i) = i2
Probe sequence:
0th probe = h(k) mod Table size
1th probe = (h(k) + 1) mod Table size
2th probe = (h(k) + 4) mod Table Size
3th probe = (h(k) + 9) mod Table Size
. . .
ith probe = (h(k) + i2) mod Table Size

16. Quadratic Probing:
Success guarantee for  < ½
• show for all 0  i,j  size/2 and i  j
(h(x) + i2) mod size  (h(x) + j2) mod size
• by contradiction: suppose that for some i  j:
(h(x) + i2) mod size = (h(x) + j2) mod size
 i2 mod size = j2 mod size
 (i2 - j2) mod size = 0
 [(i + j)(i - j)] mod size = 0
Because size is prime(i-j)or (i+j) must be zero, and
neither can be

17. OPEN ADDRESSING HASH TABLE WITH
QUADRATIC PROBING
Empty table After 89 After 18 After 49 After 58 After 69
0 49 49 49
1
2 58 58
3 69
4
5
6
7
8 18 18 18 18
9 89 89 89 89 89

18. DOUBLE HASHING
The last collision resolution method
examine is double hashing.
Double hashing f(i)=i⋅hash2(x).
Hash function to x and probe at a distance
hash2(x),2hash2(x)…,
A function such as hash2(x)=R-(x mod R),
with R a prime smaller than Table Size.

19. f(i) = i * g(k)
where g is a second hash function
Probe sequence:
0th probe = h(k) mod Table Size
1th probe = (h(k) + g(k)) mod Table Size
2th probe = (h(k) + 2*g(k)) mod Table Size
3th probe = (h(k) + 3*g(k)) mod Table Size
. . .
ith probe = (h(k) + i*g(k)) mod Table Size

20. Resolving Collisions with Double
Hashing
 Insert these values into the hash table in this order.
Resolve any collisions with double hashing:
13
28
33
147
43
Hash Functions:
H(K) = K mod M
H2(K) = 1 + ((K/M) mod (M-1))

21. THANK YOU