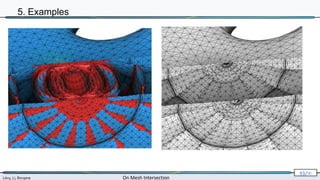
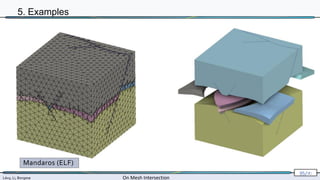
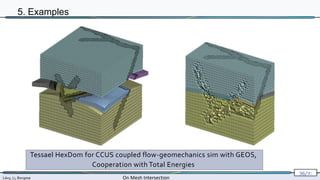
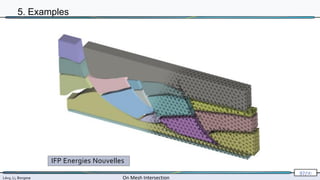
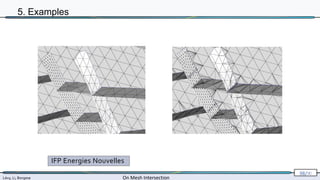
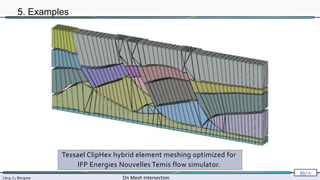
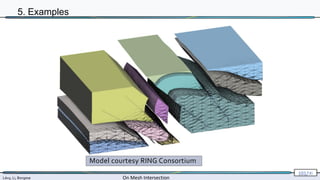
The document presents research by Lévy, Li, and Borgese on efficient and robust methods for mesh intersection. It covers algorithmic approaches for identifying intersecting triangles, including candidate selection, triangle-triangle intersection handling, and re-triangulation using constrained Delaunay triangulation strategies. The content is technical, referencing various configurations, computational techniques, and their implementation in programming contexts.


![Lévy, Li, Borgese On Mesh Intersection
4/∞
Lévy, Li, Borgese On Mesh Intersection
4/∞
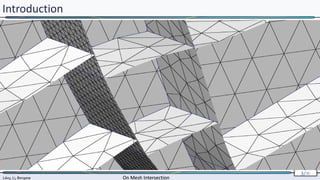
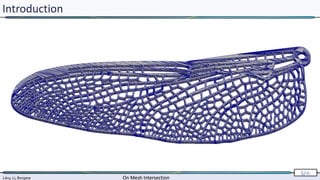
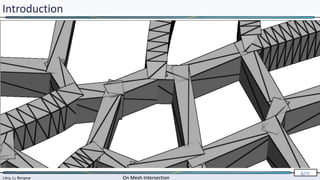
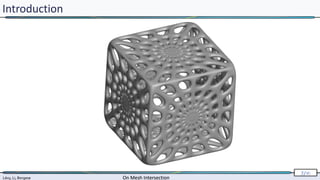
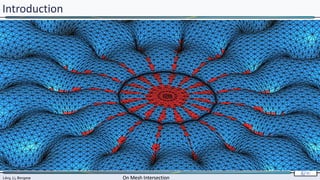
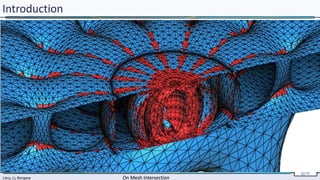
Introduction
Gocad’s “cut” functionality :
[Sword 1996]
[Caumon, Sword, Mallet 2003]
[Legentil et.al. 2022]
[Mallet 2002]
A stream of articles :
[Cherchi, Livesu, Attene
2020-2022]](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-4-320.jpg)
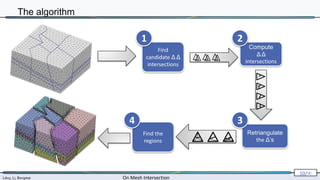

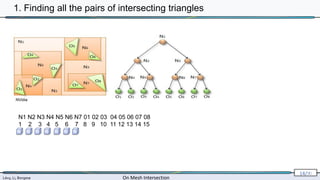
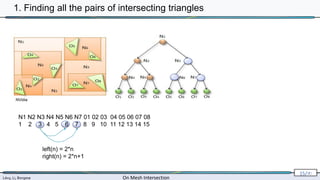
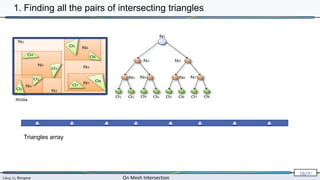
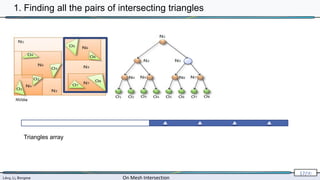
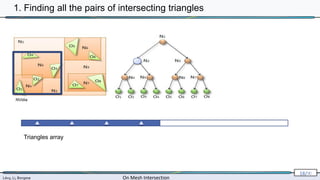
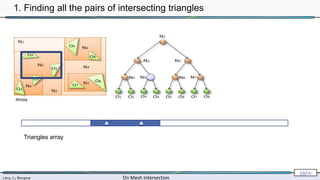
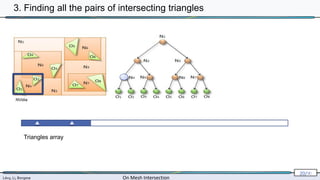
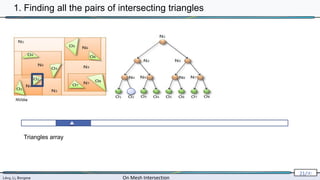
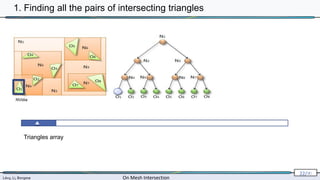
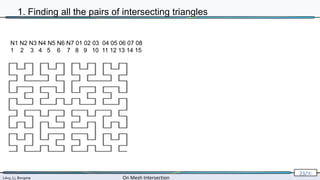
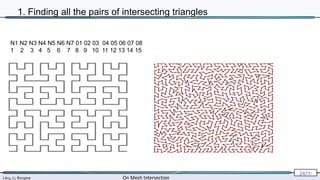
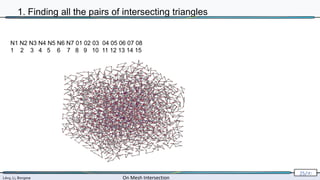
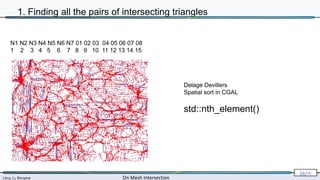


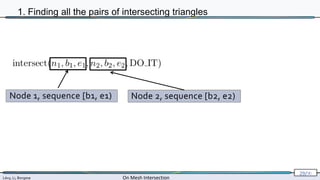
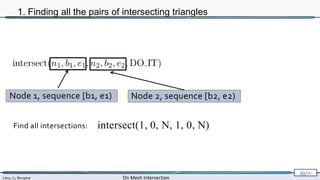
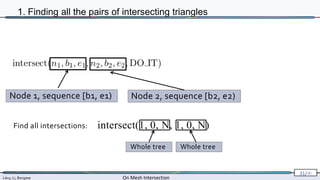



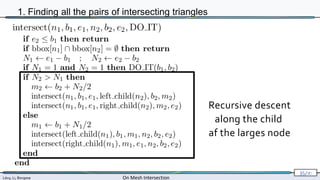
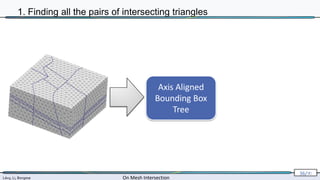
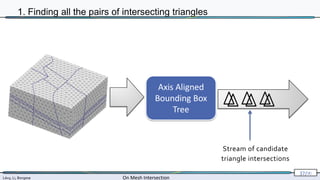


![Lévy, Li, Borgese On Mesh Intersection
54/∞
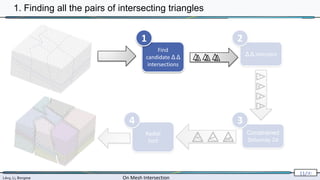
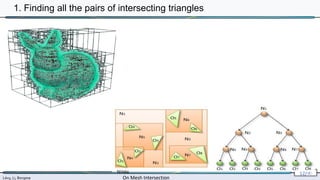
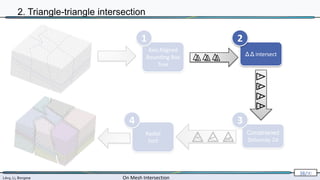
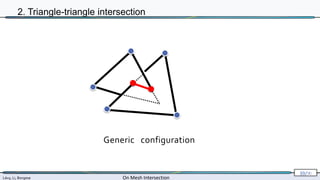
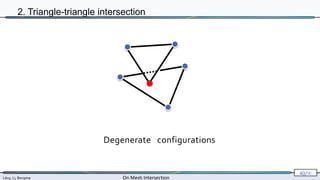
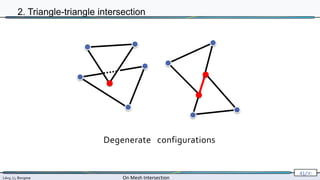
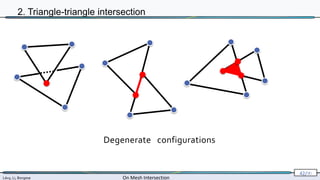
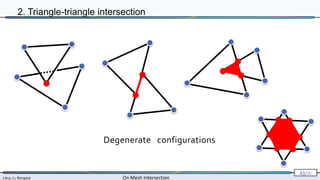
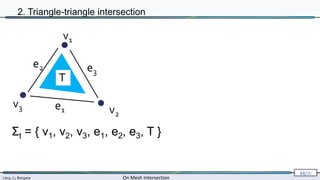
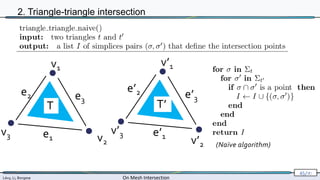
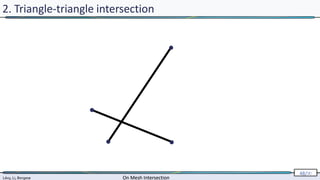
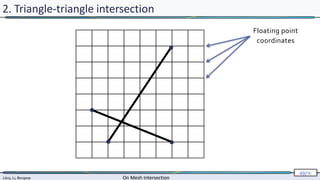
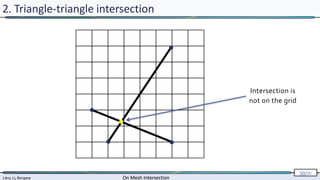
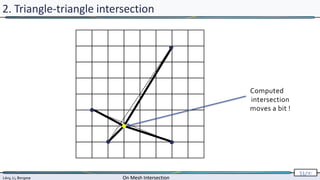
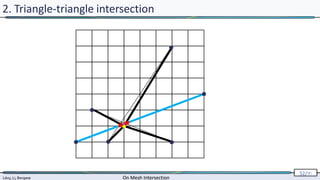
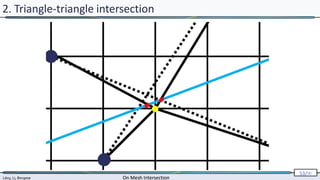
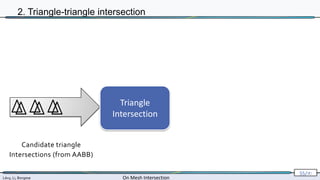
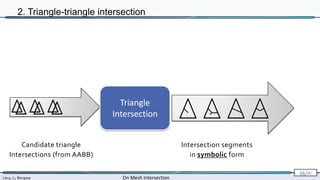
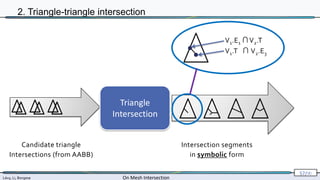
2. Triangle-triangle intersection
computed exactly
[Shewchuk 96,97]](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-54-320.jpg)

![Lévy, Li, Borgese On Mesh Intersection
64/∞
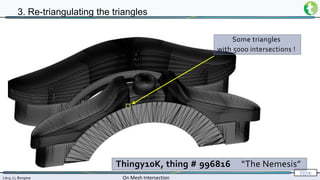
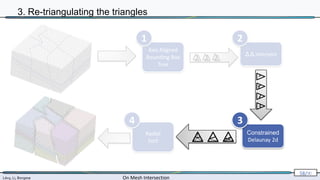
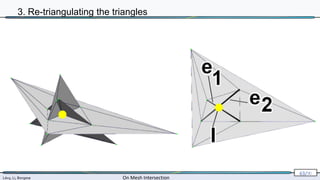
3. Re-triangulating the triangles
[Sloan 1992]](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-64-320.jpg)
![Lévy, Li, Borgese On Mesh Intersection
65/∞
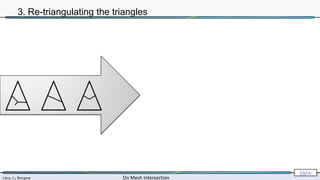
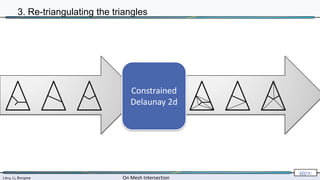
3. Re-triangulating the triangles
[Sloan 1992]](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-65-320.jpg)

![Lévy, Li, Borgese On Mesh Intersection
71/∞
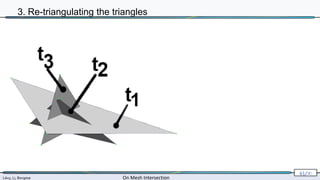
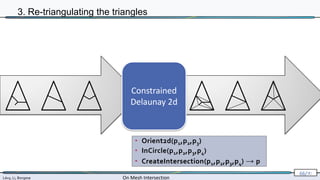
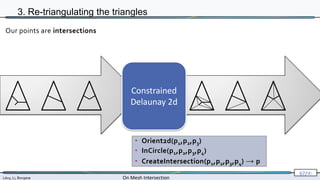
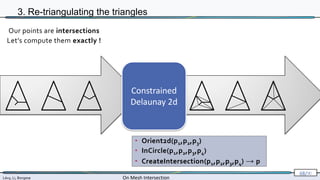
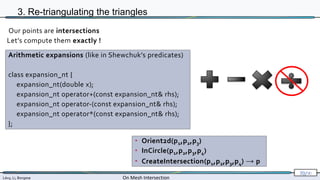
3. Re-triangulating the triangles
• Orient2d(p1,p2,p3)
• InCircle(p1,p2,p3,p4)
• CreateIntersection(p1,p2,p3,p4) → p
Our points are intersections
Let’s compute them exactly !
Arithmetic expansions (like in Shewchuk’s predicates)
class expansion_nt {
expansion_nt(double x);
expansion_nt operator+(const expansion_nt& rhs);
expansion_nt operator-(const expansion_nt& rhs);
expansion_nt operator*(const expansion_nt& rhs);
};
How to divide ?
Homogeneous coordinates !
(like in OpenGL)
[x y z w]
↕
[ x/w y/w z/w ]](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-71-320.jpg)
![Lévy, Li, Borgese On Mesh Intersection
72/∞
3. Re-triangulating the triangles
• Orient2d(p1,p2,p3)
• InCircle(p1,p2,p3,p4)
• CreateIntersection(p1,p2,p3,p4) → p
How to make it faster ?
Arithmetic expansions (like in Shewchuk’s predicates)
class expansion_nt {
expansion_nt(double x);
expansion_nt operator+(const expansion_nt& rhs);
expansion_nt operator-(const expansion_nt& rhs);
expansion_nt operator*(const expansion_nt& rhs);
};
How to divide ?
Homogeneous coordinates !
(like in OpenGL)
[x y z w]
↕
[ x/w y/w z/w ]](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-72-320.jpg)
![Lévy, Li, Borgese On Mesh Intersection
73/∞
3. Re-triangulating the triangles
• Orient2d(p1,p2,p3)
• InCircle(p1,p2,p3,p4)
• CreateIntersection(p1,p2,p3,p4) → p
How to make it faster ?
Arithmetic expansions (like in Shewchuk’s predicates)
class expansion_nt {
expansion_nt(double x);
expansion_nt operator+(const expansion_nt& rhs);
expansion_nt operator-(const expansion_nt& rhs);
expansion_nt operator*(const expansion_nt& rhs);
};
How to divide ?
Homogeneous coordinates !
(like in OpenGL)
[x y z w]
↕
[ x/w y/w z/w ]
class interval_nt
filter](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-73-320.jpg)
![Lévy, Li, Borgese On Mesh Intersection
74/∞
3. Re-triangulating the triangles
• Orient2d(p1,p2,p3)
• InCircle(p1,p2,p3,p4)
• CreateIntersection(p1,p2,p3,p4) → p
How to make it faster ?
Arithmetic expansions (like in Shewchuk’s predicates)
class expansion_nt {
expansion_nt(double x);
expansion_nt operator+(const expansion_nt& rhs);
expansion_nt operator-(const expansion_nt& rhs);
expansion_nt operator*(const expansion_nt& rhs);
};
How to divide ?
Homogeneous coordinates !
(like in OpenGL)
[x y z w]
↕
[ x/w y/w z/w ]
class interval_nt
filter
Does it always work ?
What about
overflows / underflows ?](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-74-320.jpg)
![Lévy, Li, Borgese On Mesh Intersection
75/∞
3. Re-triangulating the triangles
• Orient2d(p1,p2,p3)
• InCircle(p1,p2,p3,p4)
• CreateIntersection(p1,p2,p3,p4) → p
How to make it faster ?
Arithmetic expansions (like in Shewchuk’s predicates)
class expansion_nt {
expansion_nt(double x);
expansion_nt operator+(const expansion_nt& rhs);
expansion_nt operator-(const expansion_nt& rhs);
expansion_nt operator*(const expansion_nt& rhs);
};
How to divide ?
Homogeneous coordinates !
(like in OpenGL)
[x y z w]
↕
[ x/w y/w z/w ]
class interval_nt
filter
Does it always work ?
What about
overflows / underflows ?
multiprecision
class exact_nt](https://image.slidesharecdn.com/mathiasintersections-231222063716-8f2e20bf/85/On-Mesh-Intersection-exact-computation-and-efficiency-75-320.jpg)