Three sentences: The document summarizes techniques for meshing and re-meshing used in computer graphics. It discusses using Voronoi diagrams and Delaunay triangulations to reconstruct meshes from point clouds, and using centroidal Voronoi tessellations to improve existing meshes through re-meshing by minimizing quantization noise. The document outlines methods for reconstruction, re-meshing scanned meshes, and converting meshes to subdivision surfaces.

1. Meshing for Computer Graphics
International Meshing Roundtable 2012 - short course
Bruno Lévy
ALICE Géométrie & Lumière
CENTRE INRIA Nancy Grand-Est

2. Recommended books:
Polygon Mesh Processing, Botsch, Kobbelt, Pauly, Alliez, L., CRC Press
Delaunay triangulation and meshing, George & Borouchaku, Hermes
Le Maillage Facile, Frey & George, Hermes
Algorithmic Geometry, Boissonnat & Yvinec, Cambridge U. Press
Delaunay Mesh Generation, Cheng, Dey, Shewchuk, CRC Press
See also this survey paper:
State of the art in quad meshing, Bommes, L., Pietroni, Puppo, Silva, Tarini, Zorin,
Eurographics State of the Art report, 2012

3. Introduction - Motivations
1

4. Part 1. Motivations meshes in C.G.
Two classes of meshes used in computer Graphics:

5. Part 1. Motivations meshes in C.G.
Designed meshes subdivision surfaces

6. Part 1. Motivations meshes in C.G.
Designed meshes subdivision surfaces

7. Part 1. Motivations meshes in C.G.
Designed meshes subdivision surfaces
See also

8. Part 1. Motivations meshes in C.G.
Designed meshes subdivision surfaces

9. Part 1. Motivations meshes in C.G.
Designed meshes subdivision surfaces
+

10. Part 1. Motivations meshes in C.G.
Designed meshes subdivision surfaces
+ =

11. Part 1. Motivations meshes in C.G.
Designed meshes subdivision surfaces

12. Part 1. Motivations meshes in C.G.
Scanned meshes

13. Part 1. Motivations meshes in C.G.
Two classes of meshes used in computer Graphics:
Some Meshing Topics in Computer Graphics:
Reconstruction (from pointsets to surfaces)
Improving the quality of a mesh (re-meshing)
Computing tex. coordinates / reverse engineering
Quad remeshing / mesh to subd. surface conversion

14. Part 1. Motivations reconstruction
Output of the 3D scanner (points)

15. Part 1. Motivations reconstruction
Output of the 3D scanner (points) Triangulated mesh

16. Part 1. Motivations re-meshing
(Re)-meshing [Du et.al], [Alliez et.al], [Yan et.al ]

17. Creating a CAD model from a real car ...
1970's: purely manual acquisition (Y. Sutherland)
Part 1. Motivations reverse engineering

18. 3D laser scanner Reconstructed shape
1 million vertices, 2 million triangles:
Cannot be used in CAD/CAM software
Creating a CAD/CAM model of a car
Part 1. Motivations reverse engineering

19. Splines (cubic equations)
Q: How can we "find the equation" of this car ?
output of the scanner CAD/CAM representation
Part 1. Motivations reverse engineering

20. u
vRI
3
RI
2
S
Object space (3D) Texture space (2D)
u(x,y,z)
x(u,v)
Notion of parameterization
Part 1. Motivations
Parameterization

21. Part 1. Motivations - Parameterization
Converting a mesh into a parametric representation

22. Converting a scanned mesh into a subdivision surface
Part 1. Motivations - Parameterization
See also Tom keynote -Splines

23. Part 1. Overview
Creating a mesh from a pointset
Reconstruction
Improving an initial mesh (scanned or modeled)
Re-meshing
Computing texture coordinates for a mesh
Parameterization
Converting a scanned mesh into a subdivision surface
Global Parameterization and Quad Remeshing

24. Reconstruction
From pointsets to surfaces
2

25. Output of the scanner
(after merging)
Part 2. Reconstruction

26. Introduction
Q1: how to
connect the points ?
Part 2. Reconstruction

27. Introduction
Q2: how to
improve the mesh ?
Part 2. Reconstruction coming next (3.)

28. Introduction
Q2: how to
improve the mesh ?
Part 2. Reconstruction coming next (3.)

29. Introduction
See also:
Jonathan Shewchuk course
Jean-François Remacle course
Part 2. Reconstruction coming next (3.)

30. Part 2. Reconstruction

31. Intuitively: based on proximity
Part 2. Reconstruction

32. Voronoi diagram
X = (x1, x2, xn) set of points
xi = (xi,yi) one of the points
Part 2. Reconstruction

33. X = (x1, x2, xn) set of points
xi = (xi,yi) one of the points
Vor(i) = { x / d(x,xi) < d(x,xj) } j
Voronoi diagram
Part 2. Reconstruction

34. X = (x1, x2, xn) set of points
xi = (xi,yi) one of the points
Vor(i) = { x / d(x,xi) < d(x,xj) } j
Euclidean distance
Voronoi diagram
Part 2. Reconstruction

35. Voronoi diagram
Part 2. Reconstruction

36. Voronoi diagram of two points
x1
x2
Part 2. Reconstruction

37. Voronoi diagram of two points
x1
x2
Part 2. Reconstruction

38. Voronoi diagram of two points
x1
x2
Vor(x1):
d(x,x1) < d(x,x2)
Part 2. Reconstruction

39. Voronoi diagram of two points
x1
x2
Vor(x2):
d(x,x2) < d(x,x1)
Part 2. Reconstruction

40. Voronoi diagram of two points
x1
x2
Bisector:
d(x,x1) = d(x,x2)
Part 2. Reconstruction

41. Voronoi diagram of two points
x1
x2
Bisector:
d(x,x1) = d(x,x2)
Part 2. Reconstruction

42. Voronoi diagram of three points
x1
x3x2
Part 2. Reconstruction

43. Voronoi diagram of three points
x1
x3x2
Part 2. Reconstruction

44. x1
x3x2
d(x,x1) = d(x,x2)
Part 2. Reconstruction

45. x1
x3x2
d(x,x1) = d(x,x3)
Part 2. Reconstruction

46. x1
x3x2
d(x,x2) = d(x,x3)
Part 2. Reconstruction

47. x1
x3x2
p
d(p,x1) = d(p,x2) = d(p,x3)
Part 2. Reconstruction

48. x1
x3x2
p
p is the circumcenter of the triangle (x1,x2,x3)
Part 2. Reconstruction

49. Voronoi
diagram
of N points
Part 2. Reconstruction

50. Voronoi diagram
Cell
Part 2. Reconstruction
Delaunay triangulation

51. Voronoi diagram
Cell
Part 2. Reconstruction
Delaunay triangulation

52. Voronoi diagram
Cell
Part 2. Reconstruction
Delaunay triangulation

53. Voronoi diagram
Cell Vertex
Part 2. Reconstruction
Delaunay triangulation

54. Voronoi diagram
Cell
Edge
Vertex
Part 2. Reconstruction
Delaunay triangulation

55. Voronoi diagram
Cell
Edge
Vertex
Edge
Part 2. Reconstruction
Delaunay triangulation

56. Voronoi diagram
Cell
Edge
Vertex
Vertex
Edge
Part 2. Reconstruction
Delaunay triangulation

57. Voronoi diagram
Cell
Edge
Vertex
Vertex
Edge
Cell
(triangle)
Part 2. Reconstruction
Delaunay triangulation

58. Voronoi diagram
Cell
Edge
Vertex
Vertex
Edge
Cell
(triangle)
Duality
Part 2. Reconstruction
Delaunay triangulation

59. Voronoi diagram
Part 2. Reconstruction
Delaunay triangulation

60. Voronoi diagram
Part 2. Reconstruction
Delaunay triangulation

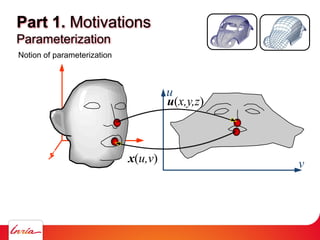
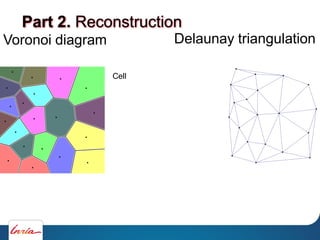
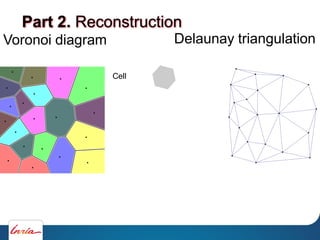
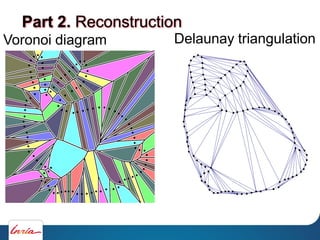
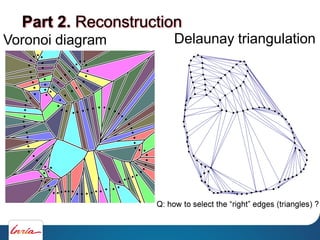
61. Voronoi diagram
Amenta et.al, 1998]
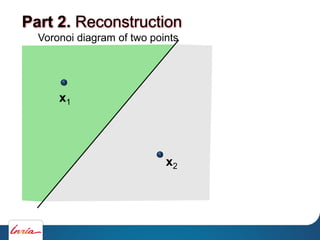
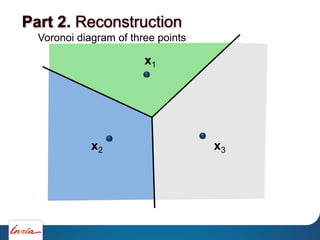
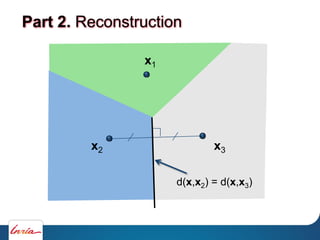
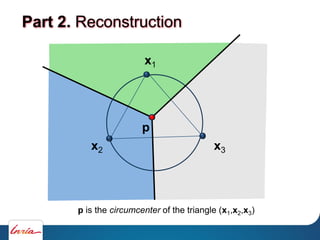
Part 2. Reconstruction
Delaunay triangulation

62. Voronoi diagram
Medial axis
Part 2. Reconstruction
Delaunay triangulation

63. Voronoi diagram Delaunay triangulation
Insert the Voronoi vertices (red) into the triangulation
Part 2. Reconstruction

64. Part 2. Reconstruction

65. tetrahedra)
Part 2. Reconstruction
A problem: in 3D the set of Voronoi vertices does not converge to the medial axis !

66. A problem: in 3D the set of Voronoi vertices does not converge to the medial axis !
tetrahedra)
Circumcenter
Part 2. Reconstruction

67. Solution: the set of poles (subset of Voronoi vertices) converge to the medial axis !
x
Part 2. Reconstruction

68. Solution: the set of poles (subset of Voronoi vertices) converge to the medial axis !
+ Pole of x cell = furthest Voronoi vertex
x
Part 2. Reconstruction

69. Solution: the set of poles (subset of Voronoi vertices) converge to the medial axis !
+ Pole of x cell = furthest Voronoi vertex
- Pole = furthest Voronoi vertex in opposite direction
x
Part 2. Reconstruction

70. Amenta et.al 98]
1)Compute Del(X)
Part 2. Reconstruction

71. Amenta et.al 98]
1)Compute Del(X)
2)Compute the poles
Part 2. Reconstruction

72. Amenta et.al 98]
1)Compute Del(X)
2)Compute the poles
3)Compute Del(X U {poles})
Part 2. Reconstruction

73. Amenta et.al 98]
1)Compute Del(X)
2)Compute the poles
3)Compute Del(X U {poles})
4)Extract the triangles
Part 2. Reconstruction

74. Amenta et.al 98]
1)Compute Del(X)
2)Compute the poles
3)Compute Del(X U {poles})
4)Extract the triangles
- Amenta, Bern, Dey]
Part 2. Reconstruction

75. 1. Reconstruction
- -sampling of S, with < 0.1
lfs(p) = d(p, medial axis)
For all point p of S, there is a point x in X
nearer to p than lfs(p)
Part 2. Reconstruction

76. 1. Reconstruction
- -sampling of S, with < 0.1
Sampling density proportional to 1/lfs
lfs measures curvature and thickness
Part 2. Reconstruction

77. 1. Reconstruction
- -sampling of S, with < 0.1
Sampling density proportional to 1/lfs
lfs measures curvature and thickness
Part 2. Reconstruction

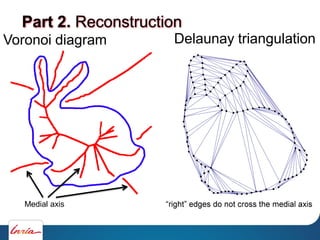
78. 1. Reconstruction
Amenta, Bern, Kamvysselis 98]
Part 2. Reconstruction

79. 1. Reconstruction
Amenta, Bern, Kamvysselis 98]
Further reading:
-
(See Nina Amenta, Tamal website)
eigencrust Kolluri and Shewchuk]
Boissonnat and Yvinec, Computational Geometry
Polygon Mesh Processing
Part 2. Reconstruction

80. 1. ReconstructionPart 2. Reconstruction
This image: Poisson Surface Reconstruction [Kahzdan et.al, SGP 2006]
Implementation in CGAL (www.cgal.org)

81. Re-meshing
Improving an existing mesh
3

82. IntroductionPart 3. Re-meshing

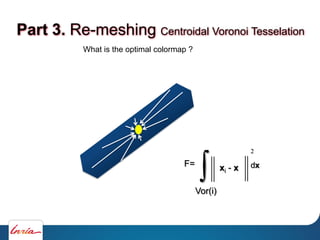
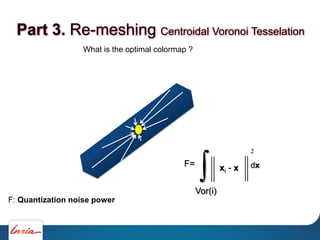
83. Part 3. Re-meshing Centroidal Voronoi Tesselation
Color quantization
[Leung et.al, GPU Pro, AK Peters, 2010]

84. R
G
B
What is the optimal colormap ?
Centroidal Voronoi Tesselation from
the information theory
Part 3. Re-meshing Centroidal Voronoi Tesselation

85. R
G
B
What is the optimal colormap ?
xi = (ri,gi,bi) Colormap entry
Part 3. Re-meshing Centroidal Voronoi Tesselation

86. R
G
B
What is the optimal colormap ?
xi = (ri,gi,bi) Colormap entry
Vor(i) = { x / d(x,xi) < d(x,xj) } i j
xi
Part 3. Re-meshing Centroidal Voronoi Tesselation

87. What is the optimal colormap ?
A « bad » colormap entry / Voronoi cell
xi
Part 3. Re-meshing Centroidal Voronoi Tesselation

88. What is the optimal colormap ?
A « bad » colormap entry / Voronoi cell
: a color poorly approximated
by the colormap entry xi
Because Vor(xi) contains
xi
Why bad ?
Part 3. Re-meshing Centroidal Voronoi Tesselation

89. What is the optimal colormap ?
Part 3. Re-meshing Centroidal Voronoi Tesselation

90. What is the optimal colormap ?
2
dx
Vor(i)
xi - xF=
Part 3. Re-meshing Centroidal Voronoi Tesselation

91. What is the optimal colormap ?
2
dx
Vor(i)
xi - xF=
F: Quantization noise power
Part 3. Re-meshing Centroidal Voronoi Tesselation

92. What is the optimal colormap ?
2
dx
Vor(i)
xi - xF=
F: Quantization noise power
Part 3. Re-meshing Centroidal Voronoi Tesselation

93. What is the optimal colormap ?
F=
Vor(i)
2
dxxi - x
i
Minimize
Part 3. Re-meshing Centroidal Voronoi Tesselation

94. The classical method:
F=
Vor(i)
2
dxxi - x
i
Part 3. Re-meshing Centroidal Voronoi Tesselation

95. The classical method:
F|xi = 2 mi (xi - gi) [Iri et.al], [Du et.al]
F=
Vor(i)
2
dxxi - x
i
Part 3. Re-meshing Centroidal Voronoi Tesselation

96. The classical method:
F|xi = 2 mi (xi - gi) [Iri et.al], [Du et.al]
Volume of Vor(i)
F=
Vor(i)
2
dxxi - x
i
Part 3. Re-meshing Centroidal Voronoi Tesselation

97. The classical method:
F|xi = 2 mi (xi - gi) [Iri et.al], [Du et.al]
Volume of Vor(i) Centroid of Vor(i)
F=
Vor(i)
2
dxxi - x
i
Part 3. Re-meshing Centroidal Voronoi Tesselation

98. The classical method:
F=
Vor(i)
2
dxxi - x
i
F|xi = 2 mi (xi - gi) [Iri et.al],
[Du et.al]
Volume of Vor(i) Centroid of Vor(i)
If xi coincides with the centroid of Vor(i),
we got a stationary point of F (therefore a « good sampling »)
Part 3. Re-meshing Centroidal Voronoi Tesselation

99. The classical method:
F=
Vor(i)
2
dxxi - x
i
F|xi = 2 mi (xi - gi) [Iri et.al],
[Du et.al]
Volume of Vor(i) Centroid of Vor(i)
If xi coincides with the centroid of Vor(i),
we got a stationary point of F (therefore a « good sampling »)
Vor(X): Centroidal Voronoi Tesselation
Part 3. Re-meshing Centroidal Voronoi Tesselation

101. (Geometric point of view)
Loop
Move the xi's to the gi's
Re-triangulate
End loop
Part 3. Re-meshing Centroidal Voronoi Tesselation

102. (Geometric point of view)
Loop
Move the xi's to the gi's
Re-triangulate
End loop
+ Provably decreases F [Du et.al]
+ Reasonably easy to implement
- Slow (linear) convergence
Part 3. Re-meshing Centroidal Voronoi Tesselation

103. Part 3.
Idea:
Use method for minimizing the non-linear function F
[Liu, Wang, L, Yan, Lu, ACM TOG 2008]

104. Part 3.
While | F | >
2
x,x F X x F= -
solve
X X + X
End while
-linear function F

105. Part 3.
While | F | >
solve
X X + X
End while
-linear function F
2
x,x F X x F= -
Gradient = 1st order derivatives

106. Part 3.
While | F | >
solve
X X + X
End while
-linear function F
Hessian = 2nd order derivatives
2
x,x F X x F= -

107. Part 3.
Theorem: F is C2 almost everywhere
[Liu, Wang, L, Sun, Yan, Lu and Yang 09]

108. Part 3.
Theorem: F is C2 almost everywhere
[Liu, Wang, L, Sun, Yan, Lu and Yang 09]
If you want to know: it is not C2 when:
A bisector is aligned with an edge of the boundary
Two sites coincide [Du, Emelinanenko et.al, 2011]

109. Part 3.
Other Newton-type solvers for CVT

110. Part 3.
Quasi-Newton solver (LBFGS)
As easy to implement as gradient descent
(Nearly) as fast as full Newton solver

111. Part 3. Newton CVT - Evaluation

112. Part 3. Newton CVT - Evaluation

113. Part 3. Newton CVT - Evaluation
Computer
precision
reached
|| F|| == 0.0

114. Part 3.
CVT in 2D

115. Part 3.

116. Part 3.
CVT in 2D
CVT on surfaces

117. Part 3.

118. Part 3.
CVT in 2D
CVT on surfaces
CVT in volumes
[Yan, Wang, L, Liu SIGGRAPH 2010]

119. Part 3.

120. 2. Remeshing
Validity of Restricted Voronoi Diagram / Restricted Delaunay Triangulation
Theorem : [Edelsbrunner & Shah 1997]
Topological Ball Property: if each face of the
Restricted Voronoi Diagram is homeomorphic to a
disc, then the Restricted Delaunay Triangulation is
homeomorphic to the surface S
Part 3.

121. Part 3.

122. 2. Remeshing
Validity of Restricted Voronoi Diagram / Restricted Delaunay Triangulation
Theorem : [Edelsbrunner & Shah 1997]
Topological Ball Property: if each k-face of the
Restricted Voronoi Diagram is homeomorphic to a
disc, then the Restricted Delaunay Triangulation is
homeomorphic to the surface S
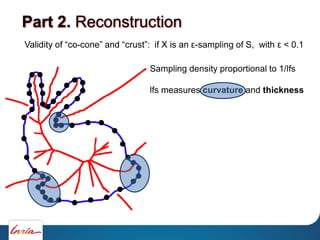
Theorem: [Amenta & Bern 1999]
if X is an -sampling of S, with < 0.1, then the Restricted
Delaunay triangulation is homeomorphic to the surface S
Part 3.

123. Part 3. Conclusions on Newton CVT
Definition (optimal sampler): Minimize F =
Vor(i)
2
dxxi - x
i

124. Part 3. Conclusions on Newton CVT
Definition (optimal sampler): Minimize F =
Vor(i)
2
dxxi - x
i
Property of the minimizer: i, xi = gi

125. Part 3. Conclusions on Newton CVT
Definition (optimal sampler): Minimize F =
Vor(i)
2
dxxi - x
i
method
for CVT
Sticking to the definition
(rather than the property)

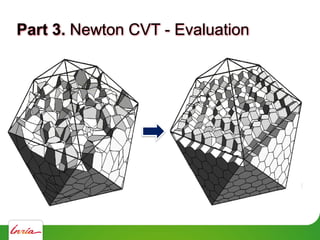
126. Part 3. Conclusions on Newton CVT
Sticking to the definition
(rather than the property)
Benefits:
Faster convergence
[Liu, Wang, L, Sun, Yan, Lu and Yang 09]
More general algorithm Chap. 4.

127. Blowing Square Bubbles
Quad remeshing with L Centroidal Voronoi Tesselations
4

128. Part 4. Lp Centroidal Voronoi Tesselation
1. Motivations Hex meshing

129. Tet Meshing
1. Fully Automated
2. Millions of elements in
minutes/seconds
3. Adequate for some analysis
4. Inaccurate for other Analysis
Hex Meshing
1. Partially Automated, some Manual
2. Millions of elements in
days/weeks/months
3. Preferred by some analysts for solution
quality
[Matt Staten] (Sandial Labs)
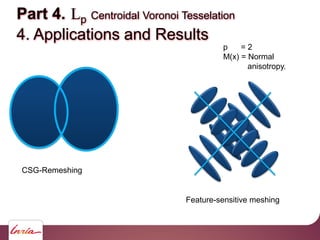
Part 4. Lp Centroidal Voronoi Tesselation
1. Motivations Why Hexes ?

130. p=2 p=4 p=8
Part 4. Lp Centroidal Voronoi Tesselation
2. Blowing Square Bubbles
See also: Research Note, this IMR, Thibaud Mouton & Eric Bechet

131. Part 4.

132. F=
Vor(i)
2
dx(xi x)
i
Standard CVT:
Part 4. Lp Centroidal Voronoi Tesselation
3. Algorithm

133. F=
Vor(i)
2
dx(xi x)
i
Standard CVT:
F=
Vor(i)
p
dxM(x) (xi x)
i p
Lp CVT:
[L and Liu 2010]
Part 4. Lp Centroidal Voronoi Tesselation
3. Algorithm

134. F=
Vor(i)
p
dxM(x) (xi x)
i p
Lp CVT:
Anisotropy, encodes desired orientation
Riemannian metric G = Mt M
Part 4. Lp Centroidal Voronoi Tesselation
3. Algorithm

135. F=
Vor(i)
p
dxM(x) (xi x)
i p
Lp CVT:
Lp norm: || x ||
p
= |x|p + |y|p + |z|p
p
Part 4. Lp Centroidal Voronoi Tesselation
3. Algorithm

136. F=
Vor(i)
p
dxM(x) (xi x)
i p
Lp CVT:
Lp norm: || x ||
p
= |x|p + |y|p + |z|p
p
= xp + yp + zpIf p is even: || x ||
p
p
Part 4. Lp Centroidal Voronoi Tesselation
3. Algorithm

137. Part 4. Lp Centroidal Voronoi Tesselation
4. Applications and Results
p = 2
M(x) = ppal dir.
of curvature.
See also: this IMR, Anisotropic CVT with VORPALINE, L and Bonneel

138. p = 2
M(x) = Normal
anisotropy.
Feature-sensitive meshing
Part 4. Lp Centroidal Voronoi Tesselation
4. Applications and Results

139. p = 2
M(x) = Normal
anisotropy.
Feature-sensitive meshing
CSG-Remeshing
Part 4. Lp Centroidal Voronoi Tesselation
4. Applications and Results

140. Part 4. Lp Centroidal Voronoi Tesselation
4. Applications and Results

141. p = 8
M(x) = ppal dir.
of curvature.
Part 4. Lp Centroidal Voronoi Tesselation
4. Applications and Results

142. Part 4. Lp Centroidal Voronoi Tesselation

143. + many other examples in paper
and supplemental material.
Part 4. Lp Centroidal Voronoi Tesselation
4. Applications and Results

144. Parameterization
Computing texture coordinates & reverse engineering
5

145. u
vRI
3
RI
2
S
Object space (3D) Texture space (2D)
u(x,y,z)
x(u,v)
Part 5. Parameterization - definition

146. RI
3
RI
2
u
v
Pi
ui ,vi
Object space (3D) Texture space (2D)
Q: How can we find all these (ui, vi)'s ?
Part 5. Parameterization triangulated mesh

147. i
j1
j2
j 2) The border is mapped to
a convex polygon
Then we got a valid mapping
(ui,vi) = ai,j(uj,vj)
j Ni
i,j ai,j > 0
ai,i = - ai,j
1) we got some coefficients ai,j
such that
Part 5. Parameterization Tutte theorem
If...

148. Tutte's theorem characterizes a familly of valid mappings
Why not using it to construct a valid mapping ?
Part 5. Parameterization

149. 1. Map the border to a convex polygon
Part 5. Parameterization

150. 1. Map the border to a convex polygon
2. Solve A u = u'
3. Solve A v = v'
Part 5. Parameterization

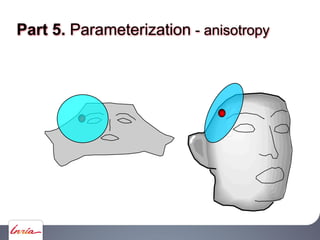
151. 1. Map the border to a convex polygon
2. Solve A u = u'
3. Solve A v = v'
Q: How do you choose
the coeffs. of A = [ai,j]
Part 5. Parameterization

152. aij
A
Problem: distortion !!!
Part 5. Parameterization How to chose aij ?

153. [Greiner et.al]: Variational principles
for geometric modeling with Splines
PDEs for geometric optimization
Can we port this principle to
the discrete setting ? [Hormann & Greiner]
Part 5. Parameterization

154. u
v
Part 5. Parameterization - anisotropy

155. v
u
u
x/ u
P
TP(S)
Part 5. Parameterization Partial derivatives

156. v
u
uv
x/ u
x/ v
P
TP(S)
Part 5. Parameterization Partial derivatives

157. u0,v0
P
w
Part 5. Parameterization Partial derivatives

158. u0,v0
P
w
Part 5. Parameterization Partial derivatives

159. u0,v0
P
w
dxP(w)
dxP(w) = / t ( x( (u0,v0)+ t.w )) )
Part 5. Parameterization Partial derivatives

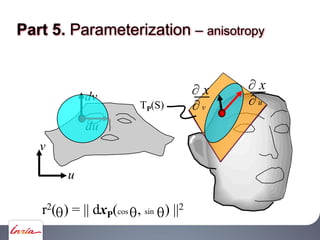
160. JP =
x/ u
y/ u
z/ u
x/ v
y/ v
z/ v
[ ]
x/ u
x/ v
P
dxP(w)
u
v
w
dxP(w) = wu x/ u + wv x/ v = JP.w
u0,v0
Part 5. Parameterization Jacobian matrix JP

161. TP(S)
V1 = dxp(w1) ; V2 = dxp(w2)
u
v
V1
V2
w1w2
Part 5. Parameterization Metric tensor GP

162. TP(S)
V1 = dxp(w1) ; V2 = dxp(w2)
u
v
V1
t V2 = (J w1)t J w2 = w1
t Jt J w2 = w1
t Gp w2
V1
V2
w1w2
Part 5. Parameterization Metric tensor GP

163. Distances : || V1 ||2 = w1
t Gp w1
Angles : V1
t V2 = w1
t Gp w2
Gp is called the metric tensor
Part 5. Parameterization measuring with GP

164. u
v
dv
du
x
u
x
vTP(S)
r2( ) = || dxP(cos , sin ) ||2
Part 5. Parameterization anisotropy

165. || dxP(w) ||2 = || JP.w ||2
= (JPw).(JPw)t
= wt.JP
t.JP.w
= wt.IP.wIP =
x
u
2
x
v
2x
u
x
v
x
u
x
v
Part 5. Parameterization Metric tensor GP

166. a
b
r2( ) = || dxP(cos w1 + sin w ) ||2
= (cos .w1 + sin .w2)t.Ip.(cos .w1 + sin .w2)
= cos2 .||w1||2. 1 + sin2 .||w2||2. 2+
sin . cos ( 1.wt
2.w1 + 2.wt
1.w2)
w1, w2 unit eigen vectors of Ip
1, 2 associated eigen values
r2( )= cos2 . 1 + sin2 . 2
Part 5. Parameterization Metric tensor GP

167. a
b r2( )= cos2 . 1 + sin2 . 2
d/d r2( ) ) = 2. sin . cos .( 2 - 1)
= sin(2 ).( 2 - 1)
a = 1 ; b = 2 (eigen values of Ip)
Part 5. Parameterization Eigen structure of GP

168. a
b
Jp =
x
u
x
v
y
u
y
v
z
u
z
v
= U V
t
a 0
0 b
0 0
Singular values decomposition (SVD) of J
Rem: Ip = Jt.J a = 1 ; b = 2
See also
[Hormann]
Part 5. Parameterization Eigen structure of GP

169. RI
3
RI
2
u
v
Pi
ui ,vi
Object space (3D) Texture space (2D)
Part 5. Parameterization Meshes

170. u
v
Part 5. Parameterization Meshes

171. u
v
Part 5. Parameterization Meshes

172. first fundamental form
eigenvalues of
singular values of (anisotropy ellipse axes)
Gp
Jp
Part 5. Parameterization Meshes

173. Define some energy functional F in function of Jp, Ip, 1, 2
Expand their expression in F in function of the unknown ui, vi
Design an algorithm to find the ui,vi's that minimizes F
Part 5. Parameterization Meshes

174. [Hormann & Greiner]
[Maillot & Verroust]
[Sander & Hoppe]
Part 5. Parameterization Meshes

175. [Hormann & Greiner]
[Maillot & Verroust]
[Sander & Hoppe]
Part 5. Parameterization Meshes

176. aij = 1
mean value coordinates[Floater]
The only one with th. guarantees
Part 5. Parameterization Meshes

177. 2 = 1
Part 5. Parameterization Conformal maps
1 = 2

178. x
u
x
v
x
v
x
u
^ N =
2 = 1
Part 5. Parameterization Conformal maps

179. u
v
u
x
=v
y
u
y
= -v
x
Cauchy-Riemann:
Part 5. Parameterization Conformal maps

180. u
v
u
x
=v
y
u
y
= -v
x
Cauchy-Riemann:
No Piecewise Linear solution in general
Part 5. Parameterization Conformal maps

181. Minimize
2
u
x
v
y
u
y-
v
x
-
T
Part 5. Parameterization Least Squares Conformal Maps
[L, Petitjean, Ray Maillot 2002]

182. Minimize
2
u
x
v
y
u
y-
v
x
-
T
Part 5. Parameterization Least Squares Conformal Maps
[L, Petitjean, Ray Maillot 2002]

183. Limits of analytic methods
distortions ; validity
Geometric methods
LSCM ; DNCP
Part 5. Parameterization Geometric Methods

184. Variables: angles
characterization of planar triangulation
Part 5. Parameterization Geometric Methods
Angle Based Flattening [Sheffer & De Sturler]

185. Cut by Seamster
[Sheffer & Hart]
initial ABF [Sheffer & de Sturler]
faster one [Sheffer et.al 04]
linABF [Zayer et.al 07]
u
v
Part 5. Parameterization Geometric Methods

186. Normal mapping
Part 5. Parameterization Geometric Methods

188. Create a « geographic coordinate system »
Part 5. Parameterization Arbitrary topology

189. Part 5. Parameterization Arbitrary topology

190. Part 5. Parameterization Arbitrary topology
From mesh to T-Splines (see also Tom keynote)

191. Part 5. Parameterization singularities

192. Archibald Higgins Adventures (used with author permission)
For french readers, Archibald is known as Anselme Lanturlu
http://www.savoir-sans-frontieres.org
Part 5. Parameterization singularities

193. Part 5. Parameterization singularities

194. Part 5. Parameterization singularities

195. Poincarré Hopf
N-Symmetry
direction fields
[Ray et.al]
See also N-Rosy
[Zhang et.al]
Part 5. Parameterization singularities

196. A N-symmetry direction field is, for each point of a surface, a set of N
unit vectors of the tangent plane that is invariant by rotation of 2 /N.
N = 1 N = 2 N = 4 N = 6
Part 5. Parameterization singularities

197. N = 1 N = 2 N = 4
Part 5. Parameterization singularities

198. Singularities generalize poles (and saddles) of vector fields.
N = 1 N = 2 N = 4 N = 6
Part 5. Parameterization singularities

199. I /2
I =1 I =-1 I =2
N = 1 N = 1 N = 1
x
y
Index of a singularity
Part 5. Parameterization singularities

200. I =1 I =-1 I =2
I =1/2 I =1/4 I =1/6
N = 2 N = 4 N = 6
N = 1 N = 1 N = 1
Part 5. Parameterization singularities

201. Arbitrary genus
Part 5. Parameterization singularities

202. Arbitrary genus additional degrees of freedom
1
2
T( 1) = 0; T( 2) = 0
1
2
T( 1) = 0; T( 2) = -1
1
2
T( 1) = -1/2; T( 2) = 0
Part 5. Parameterization singularities

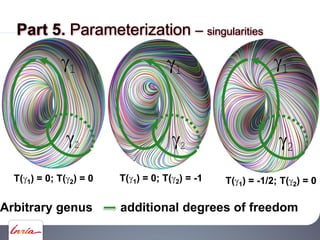
203. Extension of the Poincaré-Hopf
theorem to N-symmetry
Discrete Index theory
[Ray et.al, ACM TOG 2008]
I = 2-2g
Design with full topology control
3/4
1/4
-1/4
Controlled influence of geometry/topology [Ray et.al, ACM TOG 2009]
Index Genus
Part 5. Parameterization singularities

204. Extension of the Poincaré-Hopf
theorem to N-symmetry
Discrete Index theory
[Ray et.al, ACM TOG 2008]
I = 2-2g
Design with full topology control
3/4
1/4
-1/4
Controlled influence of geometry/topology [Ray et.al, ACM TOG 2009]
Index Genus
Part 5. Parameterization singularities
See also this IMR, Kovalski, Ledoux and Frey, PDE-based quad meshing

205. Part 5. Parameterization singularities

206. Q: How can we «integrate» a N-Symmetry direction field?
Part 5. Parameterization singularities

207. Guidance vector fields
Part 5. Parameterization singularities
Periodic Global Parameterization [Ray et.al, 2006]

208. ( ) : Parametric coordinates
Part 5. Parameterization singularities
Periodic Global Parameterization [Ray et.al, 2006]

209. Part 5. Parameterization singularities
Periodic Global Parameterization [Ray et.al, 2006]

210. Part 5. Parameterization singularities
Periodic Global Parameterization [Ray et.al, 2006]

211. Part 5. Parameterization singularities
Periodic Global Parameterization [Ray et.al, 2006]

212. Polycubemaps
Semi-manual construction[Tarini et.al]
Part 5. Parameterization quad base complex

213. Part 5. Parameterization quad meshing
More references
on quad meshing in:
State of the art in quad meshing,
Bommes, L., Pietroni, Puppo, Silva,
Tarini, Zorin,
Eurographics State of the Art report,
2012

214. Merci
Thank you for your attention
http://alice.loria.fr