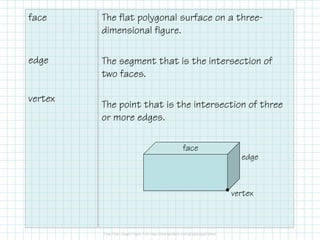
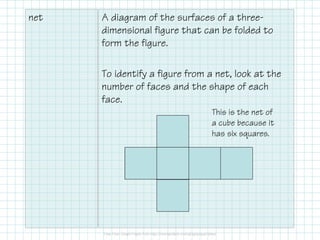
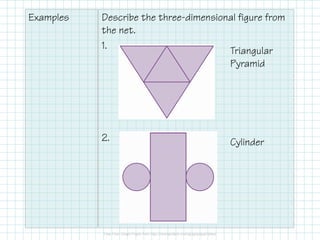
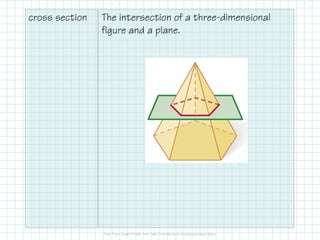
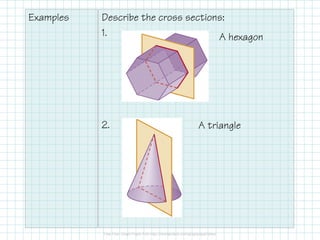
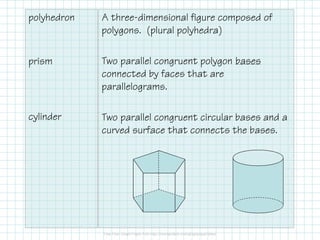
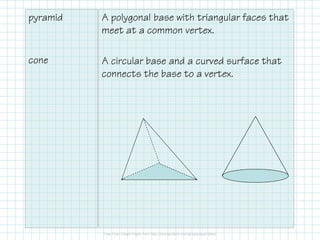
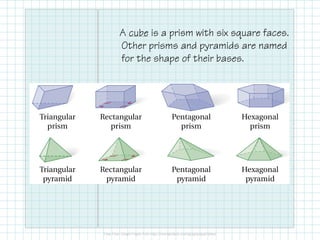
This document defines key terms and concepts in solid geometry, including: - Classifying three-dimensional figures according to their properties like faces, edges, and vertices. - Using nets and cross sections to analyze three-dimensional shapes. - Common solids like prisms, pyramids, cylinders, and their properties. - Euler's formula relating the number of vertices, edges, and faces in a polyhedron. 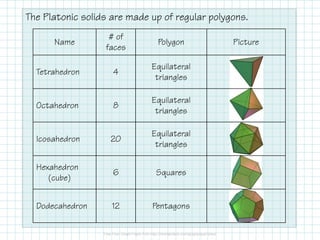- The five Platonic solids - regular polyhedra with faces of identical regular polygons.

1. Solid Geometry
The student is able to (I can):
• Classify three-dimensional figures according to their
properties.
• Use nets and cross sections to analyze three-dimensional
figures.

2. face
edge
vertex
The flat polygonal surface on a three-
dimensional figure.
The segment that is the intersection of
two faces.
The point that is the intersection of three
or more edges.
face
edge
vertex•

3. polyhedron
prism
cylinder
A three-dimensional figure composed of
polygons. (plural polyhedra)
Two parallel congruent polygon bases
connected by faces that are
parallelograms.
Two parallel congruent circular bases and a
curved surface that connects the bases.

4. pyramid
cone
A polygonal base with triangular faces that
meet at a common vertex.
A circular base and a curved surface that
connects the base to a vertex.

5. A cube is a prism with six square faces.
Other prisms and pyramids are named
for the shape of their bases.

6. net A diagram of the surfaces of a three-
dimensional figure that can be folded to
form the figure.
To identify a figure from a net, look at the
number of faces and the shape of each
face.
This is the net of
a cube because it
has six squares.

7. Examples Describe the three-dimensional figure from
the net.
1.
2.
Triangular
Pyramid
Cylinder

8. cross section The intersection of a three-dimensional
figure and a plane.

9. Examples Describe the cross sections:
1.
2.
A hexagon
A triangle

10. Euler’s
Formula
For any polyhedron with V vertices, E edges,
and F faces, V − E + F = 2.
Example: If a given polyhedron has 12
vertices and 18 edges, how many faces
does it have?
− + =
− + =
=
V E F 2
12 18 F 2
F 8

11. The Platonic solids are made up of regular polygons.
Name
# of
faces
Polygon Picture
Tetrahedron 4
Equilateral
triangles
Octahedron 8
Equilateral
triangles
Icosahedron 20
Equilateral
triangles
Hexahedron
(cube)
6 Squares
Dodecahedron 12 Pentagons