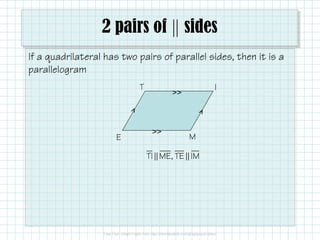
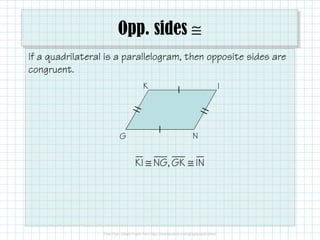
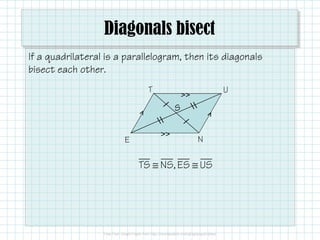
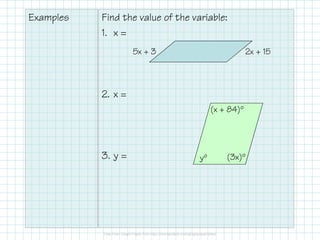
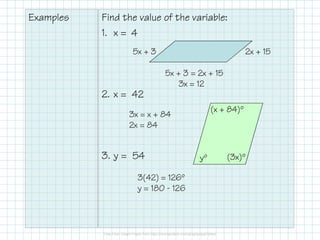
The document provides the properties and conditions of parallelograms, including definitions, congruencies of sides and angles, and the nature of diagonals. It outlines that opposite sides are parallel and congruent, opposite angles are congruent, consecutive angles are supplementary, and diagonals bisect each other. It also includes examples for proving quadrilaterals are parallelograms and solving for variables.

1. Obj. 26 Parallelograms
The student is able to (I can):
• Prove and apply properties of parallelograms.
• Use properties of parallelograms to solve problems.
• Prove that a given quadrilateral is a parallelogram.

2. parallelogram
A quadrilateral with two pairs of parallel
sides.
A parallelogram has the following
properties:
Opposite sides are parallel. (Definition)
Opposite sides are congruent.
Opposite angles are congruent.
Consecutive angles are supplementary.
Diagonals bisect each other.

3. 2 pairs of sides
If a quadrilateral has two pairs of parallel sides, then it is a
parallelogram
T
>>
E
I
>>
M
TI ME, TE IM

4. Opp. sides ≅
If a quadrilateral is a parallelogram, then opposite sides are
congruent.
K
G
I
N
KI ≅ NG, GK ≅ IN

5. Opp. angles ≅
If a quadrilateral is a parallelogram, then opposite angles are
congruent.
K
>>
G
O
>>
N
∠K ≅ ∠N, ∠O ≅ ∠G

6. Cons. angles supp.
If a quadrilateral is a parallelogram, then consecutive angles
are supplementary.
1
4
2
3
m∠1 + m∠2 = 180°
m∠2 + m∠3 = 180°
m∠3 + m∠4 = 180°
m∠4 + m∠1 = 180°

7. Diagonals bisect
If a quadrilateral is a parallelogram, then its diagonals
bisect each other.
T
U
>>
S
>>
E
N
TS ≅ NS, ES ≅ US

8. Examples
Find the value of the variable:
1. x =
5x + 3
2x + 15
2. x =
(x + 84)º
3. y =
yº
(3x)º

9. Examples
Find the value of the variable:
1. x = 4
5x + 3
2x + 15
5x + 3 = 2x + 15
3x = 12
2. x = 42
(x + 84)º
3x = x + 84
2x = 84
3. y = 54
3(42) = 126º
y = 180 - 126
yº
(3x)º

10. Conditions for Parallelograms
If one pair of opposite sides of a quadrilateral is congruent
and parallel then the quadrilateral is a parallelogram.
parallel,
We can also use the converses of the theorems from the
previous section to prove that quadrilaterals are
parallelograms.
Parallelogram
⇔
Opposite sides ≅
Opposite angles ≅
Cons. ∠s supp.
Diagonals bisect