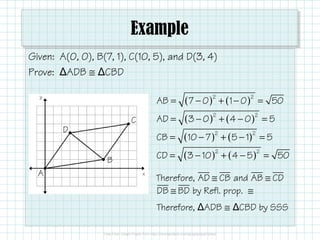
The student is able to prove conjectures about geometric figures on a coordinate plane using coordinate proofs. A coordinate proof uses coordinate geometry and algebra by placing a figure in the coordinate plane and using properties like slope, distances between points, and coordinates of vertices to prove statements about the figure. For example, a coordinate proof can show that the diagonals of a rectangle bisect each other by finding the midpoints of the diagonals have the same coordinates.

1. Obj. 20 Coordinate Proof
The student is able to (I can):
• Prove conjectures about geometric figures on a
coordinate plane

2. coordinate
proof
A style of proof that uses coordinate
geometry and algebra. Once a figure is
placed in the coordinate plane, we can use
slope, the coordinates of the vertices, the
Distance Formula, or the Midpoint Formula
to prove statements about the figure.
Example
Given: Rectangle ABCD with A(0, 0),
B(4, 0), C(4, 10), and D(0, 10)
Prove: The diagonals bisect each other.
The midpoint of AC is (2, 5), and the
midpoint of BD is also (2, 5). Therefore,
the two diagonals bisect each other.

3. Example
Given: A(0, 0), B(7, 1), C(10, 5), and D(3, 4)
Prove: ADB ≅ CBD
2
2
AB = ( 7 − 0 ) + ( 1 − 0 ) = 50
C
D
2
2
2
CB = ( 10 − 7 ) + ( 5 − 1) = 5
2
B
A
2
AD = ( 3 − 0 ) + ( 4 − 0 ) = 5
2
CD = ( 3 − 10 ) + ( 4 − 5 ) = 50
Therefore, AD ≅ CB and AB ≅ CD
DB ≅ BD by Refl. prop. ≅
Therefore, ADB ≅ CBD by SSS