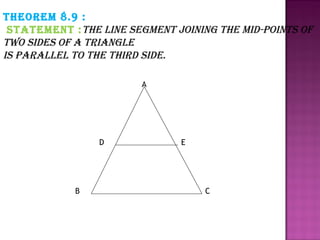
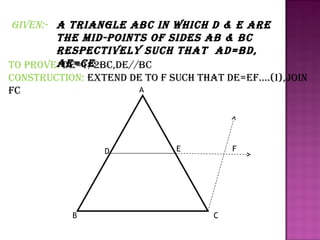
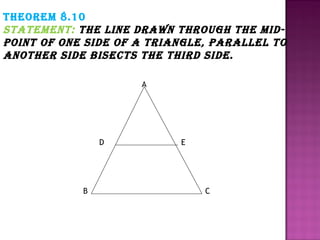
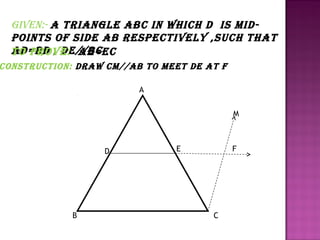
The document presents the proof of two theorems regarding lines and segments in a triangle: 1. The line segment joining the midpoints of two sides of a triangle is parallel to the third side. This is proved using properties of parallel lines and corresponding angles. 2. The line drawn through the midpoint of one side of a triangle, parallel to another side, bisects the third side. This is proved using angle-angle-side congruence and corresponding angles of parallel lines.

2. Theorem 8.9 :
STaTemenT : The line SegmenT joining The mid-poinTS of
Two SideS of a Triangle
iS parallel To The Third Side.
A
D
B
E
C

3. giVen:- a Triangle aBC in whiCh d & e are
The mid-poinTS of SideS aB & BC
reSpeCTiVelY SuCh ThaT ad=Bd,
ae=Ce
To proVe: de=1/2BC,de//BC
ConSTruCTion: exTend de To f SuCh ThaT de=ef....(i),join
A
fC
D
B
E
F
C

4. Proof: Δ AED & Δ CEF
DE=EF
∠ AED = ∠ CEF
AE=EC
Δ AED ≅ Δ CEF
∠DAE= ∠ ECF
AD=CF
(by eq no i)
(V.O.A)
(given)
(by SAS)
(by CPCT)......(ii)
(by CPCT)......(iii)
But ∠ DAE &∠ ECF are A.I.A
∴AB//CF
∴ED//CF
=> AD=BD ……….(iv)(given)
from eq (iii) & (iv)
BD=CF
Therefore, BD=CF,BD//CF
⇒BDCF is //gm
∴DE//BC (DE is part of DF)
⇒DF=DE + EF
= DF=DE + DE (DE=EF)
= DF=2DE
= 1/2DF=DE
= 1/2BC=DE (opp. Sides of //gm are equal)
=>1/2DE=BC,DE//BC
Hece,Proved

5. Theorem 8.10
STaTemenT: The line drawn Through The midpoinT of one Side of a Triangle, parallel To
anoTher Side biSecTS The Third Side.
A
D
B
E
C

6. giVen:- a Triangle abc in which d iS midpoinTS of Side ab reSpecTiVely ,Such ThaT
ad=bd , de//bc
To proVe: ae=ec
conSTrucTion: draw cm//ab To meeT de aT f
A
M
D
B
E
F
C

7. Proof: Δ AED & Δ CEF
∠ AED = ∠ CEF
(V.O.A)
∠ ADE= ∠ EFC
(A.I.A)
AD=FC
(∴ DB=FC,DB=DA)
Δ AED ≅ Δ CEF
(by ASA)
⇒AE=CE
⇒ Hence,Proved