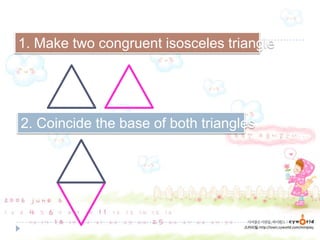
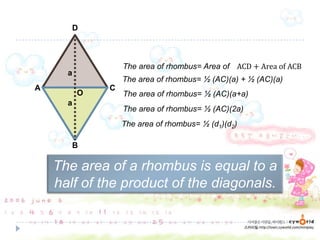
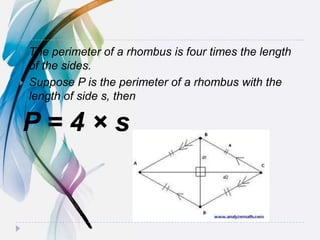
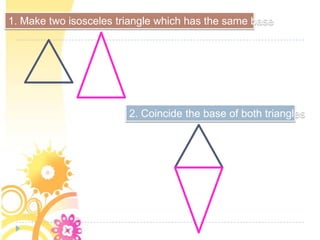
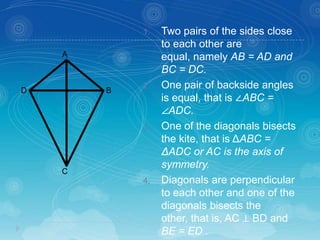
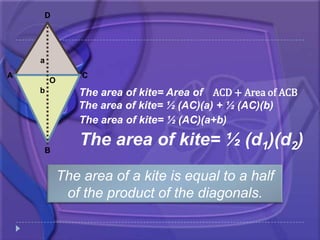
1. The document discusses formulas for calculating the perimeter and area of various shapes including rectangles, squares, rhombi, kites, and parallelograms. It provides the definitions and properties of these shapes. 2. Examples are given for calculating perimeter and area of rectangles with different dimensions. Exercises are also provided for finding missing values of rhombi, kites and parallelograms given some known information. 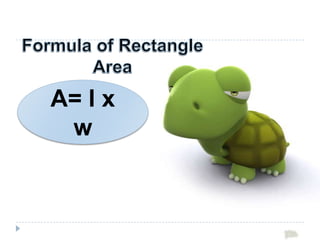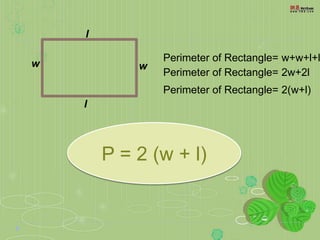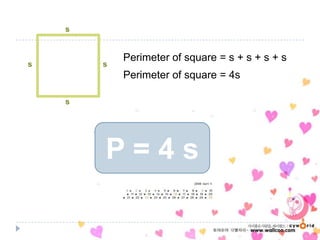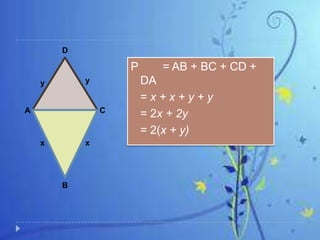3. The key formulas presented are that the area of any shape is equal to its base times its height, and the perimeter of any shape is the sum of the lengths of all its sides.

1. Calculate The perimeter and
area of triangle and
Rectangular Shape

2. A= l x
w

3. Formula of
Perimeter

4. P = 2 (w + l)
l
w w
l
Perimeter of Rectangle= w+w+l+l
Perimeter of Rectangle= 2w+2l
Perimeter of Rectangle= 2(w+l)

5. Exercise
1. Calculate the perimeter and the area of rectangles
with the following measures:
a. Length is 17 dm and width is 7 dm.
b. Length is 20 mm and width is 5 mm.
c. Length is 25 m and width is 8 cm.

6. a c t i iv t y 2

7. D
A B
C
AB=….cm ∠AOB =.......°
BC=….cm ∠BOC =.......°
CD=….cm ∠COD =.......°
AD=….cm ∠DOA =.......°
AC=….cm ∠OAD =.......°
BD=….cm ∠OBA =.......°
∠OCB =.......°
∠ODC =.......°
∠OAB =.......°
∠OBC =.......°
∠OCD =.......°
∠ODA =.......°

8. Properties

9. 1. The opposite sides are parallel.
2. All of the angles are right angles.
3. The diagonals are equal and bisect each other.
4. All the sides are equal.
5. The diagonals 1. The opposite sides are parallel.
2. All of the angles are right angles.
3. The diagonals are equal and bisect each other.
4. All the sides are equal.
5. The diagonals bisect the angles.
6. The diagonals cross perpendicularly.

10. Definition

11. Based on those properties, we can
say that a square is a rectangle
with 4 equal sides and one of its
angle is right angle.

12. Formula of The
Area

13. A = s x s
Suppose you have a room. The room
floor is in a square shape. The floor
will be covered with square tiles.

14. Formula of
Perimeter

15. P = 4 s
s
s
s
s
Perimeter of square = s + s + s + s
Perimeter of square = 4s

16. Rhombu
s

18. D
i
nf
e
i
i
ot
n

19. If both diagonals of a quadrilateral are
perpendicular and bisect each
other, then it is called a rhombus.
Rhombus is a
quadrilateral with four
equal sides.
We can also say

20. a c t i iv t y 3

21. 1. Make two congruent isosceles triangle
2. Coincide the base of both triangles

22. Properties

23.  All sides are equal
 Opposite sides are parallel
 Vertical angles are equal
 The diagonals bisect the angles
 Both diagonals are perpendicular and bisect
each other
 Diagonals bisect the rhombus or they are the
axis lines
 The sum of the two adjacent angles is 180°

24. Formula of
The Area

25. The area of rhombus= Area of ACD + Area of ACB
The area of rhombus= ½ (AC)(a) + ½ (AC)(a)
The area of rhombus= ½ (AC)(a+a)
The area of rhombus= ½ (AC)(2a)
The area of rhombus= ½ (d1)(d2)
a
a
C
D
A
B
O
The area of a rhombus is equal to a
half of the product of the diagonals.

26. Formula of
Perimeter

27.  The perimeter of a rhombus is four times the length
of the sides.
 Suppose P is the perimeter of a rhombus with the
length of side s, then
P = 4 × s

28. Exercise
The area of rhombus
ABCD is 180 cm2 .
The length of
diagonal AC is 24
cm. what is the
length of BD?

29. Kite

30. Kite is a quadrilateral with
diagonals perpendicular to each
other and one of the diagonals
bisects the other.

31. a c t i iv t y 4

32. 1. Make two isosceles triangle which has the same base
2. Coincide the base of both triangles

33. Propertie
s

34. 1. Two pairs of the sides close
to each other are
equal, namely AB = AD and
BC = DC.
2. One pair of backside angles
is equal, that is ∠ABC =
∠ADC.
3. One of the diagonals bisects
the kite, that is ΔABC =
ΔADC or AC is the axis of
symmetry.
4. Diagonals are perpendicular
to each other and one of the
diagonals bisects the
other, that is, AC ⊥ BD and
BE = ED .
B
C
D
A

35. Formula of
The Area

36. The area of kite= Area of ACD + Area of ACB
The area of kite= ½ (AC)(a) + ½ (AC)(b)
The area of kite= ½ (AC)(a+b)
The area of kite= ½ (d1)(d2)
a
b
C
D
A
B
O
The area of a kite is equal to a half
of the product of the diagonals.

37. Formula of
Perimeter

38. P = AB + BC + CD +
DA
= x + x + y + y
= 2x + 2y
= 2(x + y)
C
D
A
B
y y
x x

39. Exercise
Find the area of a kite with its diagonal:
a. 8cm and 12cm
b. 9cm and 16cm
c. 15cm and 18cm
d. 13cm and 21cm

40. Formula of The Area

41. D
i
s
c
v
o
e r
y

42. 1. Make a parallelogram and give the identity the
base and the height!
2. Cut on line DE and move the triangle AED such
that side ad coincide side BC, ∠A becomes
supplement of ∠B, and ∠D becomes complement
of ∠C. What shape do you get?
B
D C
A
Height
(t)
Base (a)

43. 3. What can you say about the area of the rectangle
and the area of the initial parallelogram? Are they
the same?
4. What is the area of a rectangular?
5. What can you conclude about the area of
parallelogram?

44. The Area and Perimeter of Parallelogram The area of parallelogram is defined as product of
the base and the height.
 The perimeter of a parallelogram is defined as twice
of two adjacent sides of the parallelogram.
 If a parallelogram has area A, base a, adjacent side
of a is b and height t, then
A = a × t
P = 2 (a + b)

45. T
A
N
K
H
u
y
o