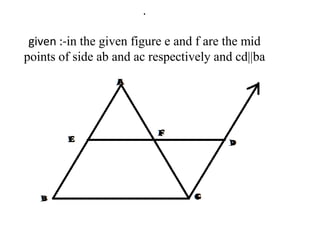
The mid-point theorem states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side. The proof uses properties of triangles, including alternate interior angles and congruence by the ASA criterion, to show that the quadrilateral formed by connecting the midpoints is a parallelogram, meaning the line segments are parallel.

1. PRESENTATION TO PROVE -

2. THE MID POINT
THEOREM
The mid point theorem state that
The line segment joining the mid
points of two sides of a triangle is
parallel to the third side

3. .
given :-in the given figure e and f are the mid
points of side ab and ac respectively and cd||ba

4. To prove :-
• The line segment joining
the mid points of two sides
of a triangle is parallel to
the third side.

5. Proof:In ∆AEF and ∆CDF
Angle EAF = CFD
(alternative interior angle)
AF = FC
(As F is the mid point of AC)
Angle AFC = DFC
(vertically opposite angles)
.∙.∆AEF is congruent to ∆CDF (ASA criteria for
congruence)
So, EF = DF
(by CPCT)
And, BE = AE
(Given)
Again, AE = DC
(by CPCT)

6. Therefore, BE = DC
(that are opposite sides
of BCDE)
As, the opposite sides of BCDE are equal
,therefore BCDE
is a parallelogram.
This gives EF||BC (As the sum of the adjacent
angles of a parallelogram is 180˚)
(Hence Proved)

7. THANK U