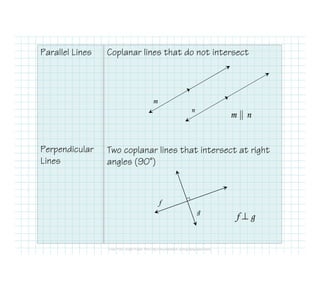
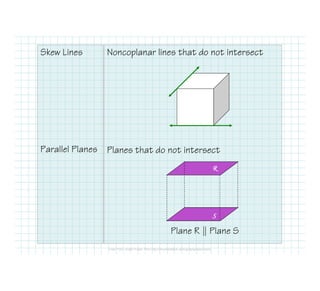
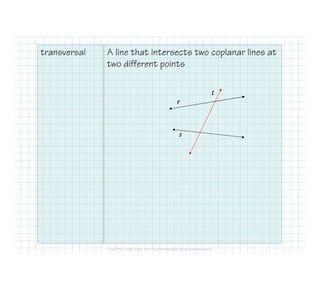
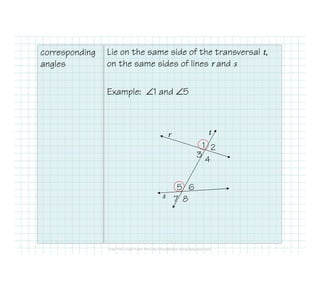
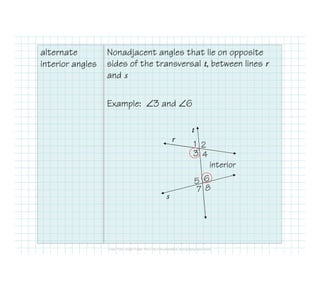
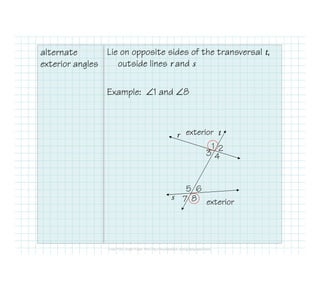
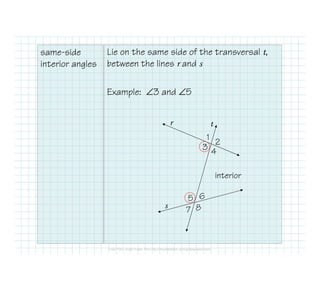
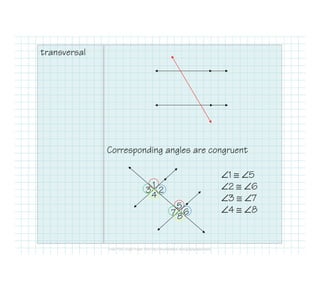
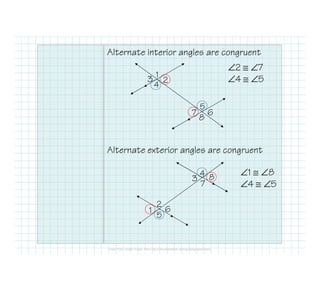
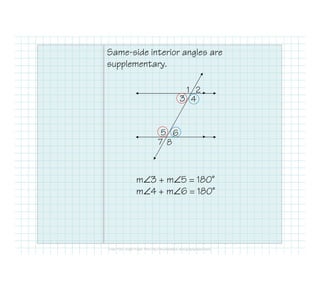
The document defines and identifies different types of lines and their relationships when intersected by a transversal line. It defines parallel lines, perpendicular lines, skew lines, and parallel planes. It also defines transversals and identifies the angle relationships that exist between corresponding angles, alternate interior angles, alternate exterior angles, and same-side interior angles when two lines are cut by a transversal. Examples are provided and properties such as corresponding angles and alternate angles being congruent are stated.

1. Obj. 12 Parallel Lines
The student is able to (I can):
• Identify parallel lines, perpendicular lines, skew lines, and
parallel planes
• Identify• Identify
— Transversals
— Corresponding angles
— Alternate Interior Angles
— Alternate Exterior Angles
— Same-side Interior Angles

2. Parallel Lines
Perpendicular
Coplanar lines that do not intersect
Two coplanar lines that intersect at right
m
n
m n
Perpendicular
Lines
Two coplanar lines that intersect at right
angles (90˚)
f
g
f ⊥ g

3. Skew Lines
Parallel Planes
Noncoplanar lines that do not intersect
Planes that do not intersectParallel Planes Planes that do not intersect
RRRR
SSSS
Plane R Plane S

4. transversal A line that intersects two coplanar lines at
two different points
r
s
t

5. corresponding
angles
Lie on the same side of the transversal t,
on the same sides of lines r and s
Example: ∠1 and ∠5
1 2
r t
87
65
4
3
1 2
s

6. alternate
interior angles
Nonadjacent angles that lie on opposite
sides of the transversal t, between lines r
and s
Example: ∠3 and ∠6
1 2
r
t
87
65
43
1 2
s
interior

7. alternate
exterior angles
Lie on opposite sides of the transversal t,
outside lines r and s
Example: ∠1 and ∠8
1 2
r texterior
87
65
43
1 2
s
exterior

8. same-side
interior angles
Lie on the same side of the transversal t,
between the lines r and s
Example: ∠3 and ∠5
3
1
2
r t
87
65
43
2
s
interior

9. transversal
Corresponding angles are congruentCorresponding angles are congruent
87 6
5
4
3
1
2
∠1 ≅ ∠5
∠2 ≅ ∠6
∠3 ≅ ∠7
∠4 ≅ ∠8

10. Alternate interior angles are congruent
Alternate exterior angles are congruent
8
7 6
5
4
3
1
2
∠2 ≅ ∠7
∠4 ≅ ∠5
Alternate exterior angles are congruent
8
7
6
5
4
3
1
2
∠1 ≅ ∠8
∠4 ≅ ∠5

11. Same-side interior angles are
supplementary.
87
65
43
1 2
87
m∠3 + m∠5 = 180˚
m∠4 + m∠6 = 180˚

12. 1. Find the measures of the
numbered angles
2. List each angle pair
corresponding angles
∠1 & ∠4; ∠2 & ∠5;
∠3 & ∠6; ∠8 & ∠7
1 2
3 125˚
(8)
Practice
m∠1 = 125˚; m∠2 = 55˚;
m∠3 = 55˚; m∠4 = 125˚;
m∠5 = 55˚; m∠6 = 55˚;
m∠7 = 125˚
∠3 & ∠6; ∠8 & ∠7
alt. interior angles
∠3 & ∠5; ∠8 & ∠4
alt. exterior angles
∠1 & ∠7; ∠2 & ∠6
same-side interior angles
∠3 & ∠4; ∠8 & ∠5
4 5
6 7