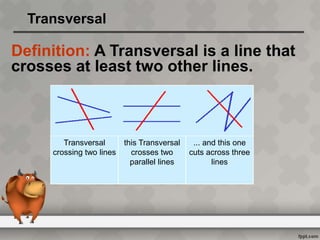
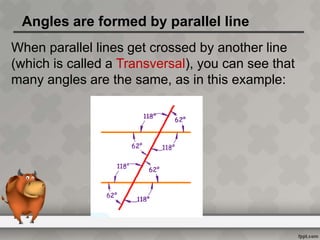
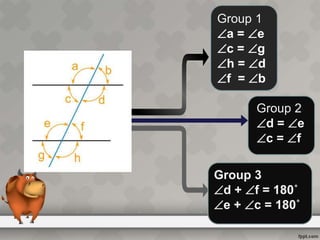
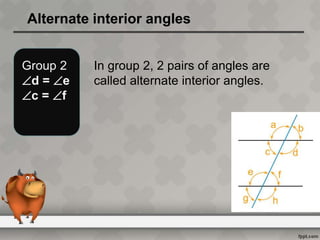
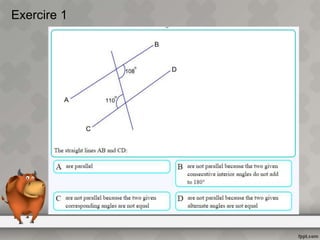
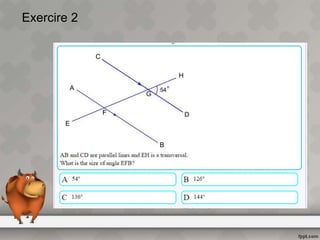
When parallel lines are crossed by a transversal, different types of angles are formed that have specific relationships. Corresponding angles are equal, as are alternate interior angles. Interior angles on the same side of the transversal but between different parallel lines sum to 180 degrees, making them supplementary. The document defines key terms like transversal and parallel lines and provides examples of the angle relationships that occur when parallel lines are cut by a transversal.

1. Angles and Parallel Lines

2. Trasversal
Parallel lines
Angles are formed
by parallel line
Angles and
Parallel Lines
1
2
3

3. Transversal
Definition: A Transversal is a line that
crosses at least two other lines.
Transversal
crossing two lines
this Transversal
crosses two
parallel lines
... and this one
cuts across three
lines

4. Paralell lines
Lines are parallel if they are always the same
distance apart (called "equidistant"), and will
never meet. Just remember:
Always the same distance apart and never
touching.The red line is parallel to the blue line in both these
cases:

5. Angles are formed by parallel line
When parallel lines get crossed by another line
(which is called a Transversal), you can see that
many angles are the same, as in this example:

6. Group 1
a = e
c = g
h = d
f = b
Group 2
d = e
c = f
Group 3
d + f = 180˚
e + c = 180˚

7. Corresponding angles
Group 1
a = e
c = g
h = d
f = b
In group 1, the 4 pairs of angles
are called corresponding angles.

8. Alternate interior angles
Group 2
d = e
c = f
In group 2, 2 pairs of angles are
called alternate interior angles.

9. Interior angles
Group 3
d + f = 180˚
e + c = 180˚
Group 3 consits of all the four
interior angles.
Thay are supplementary angles.

10. Exercire 1

11. Exercire 2