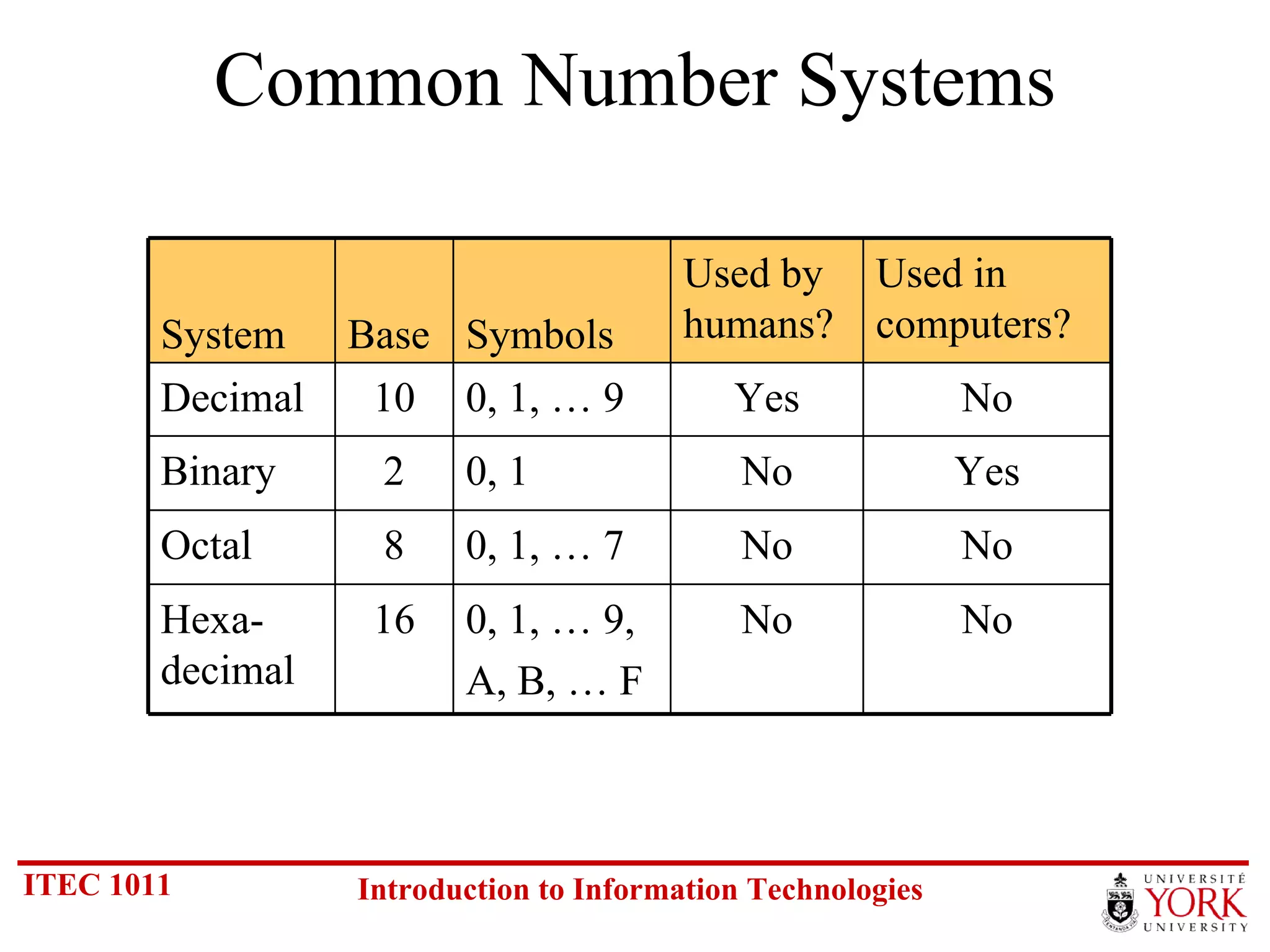
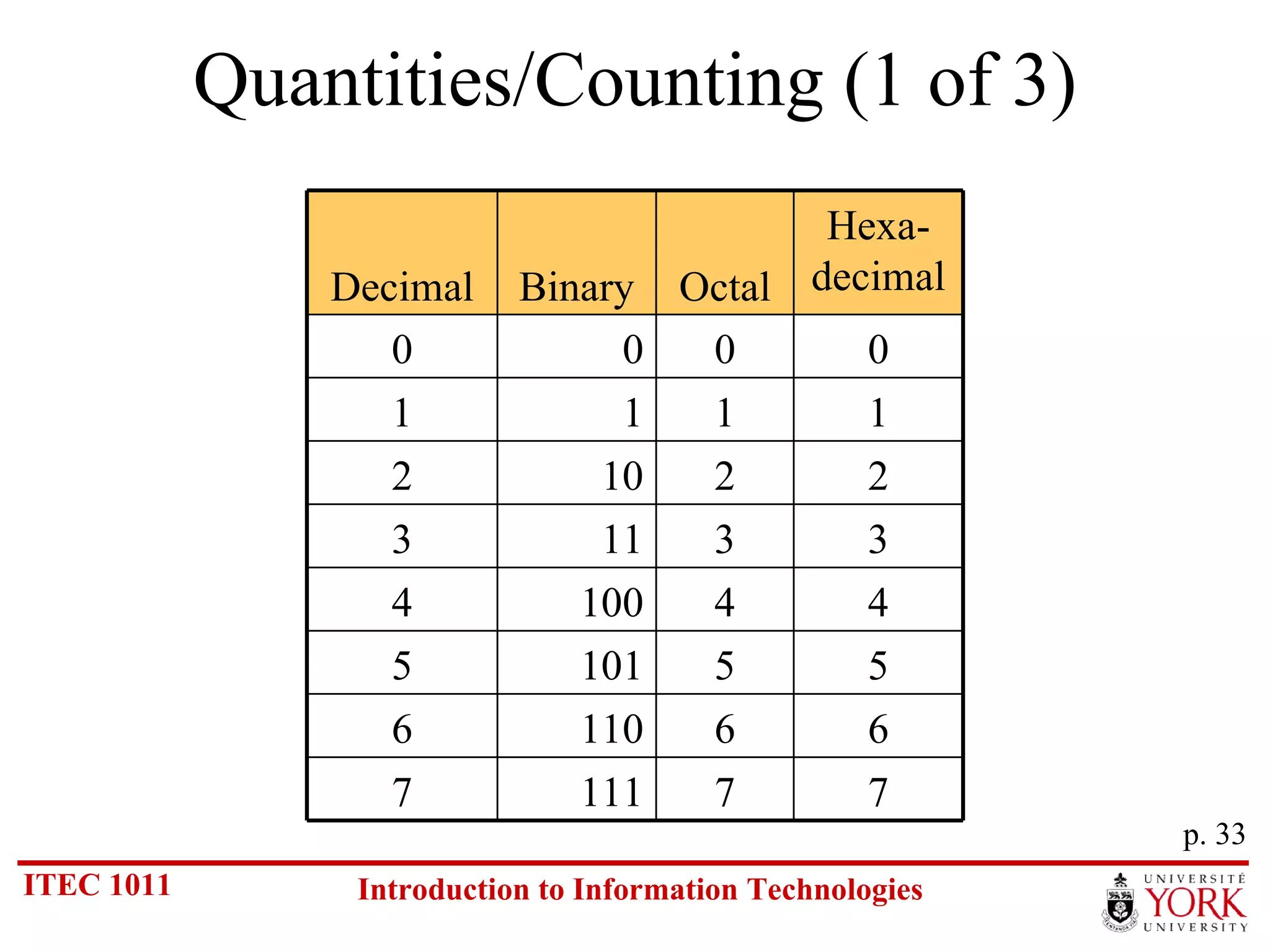
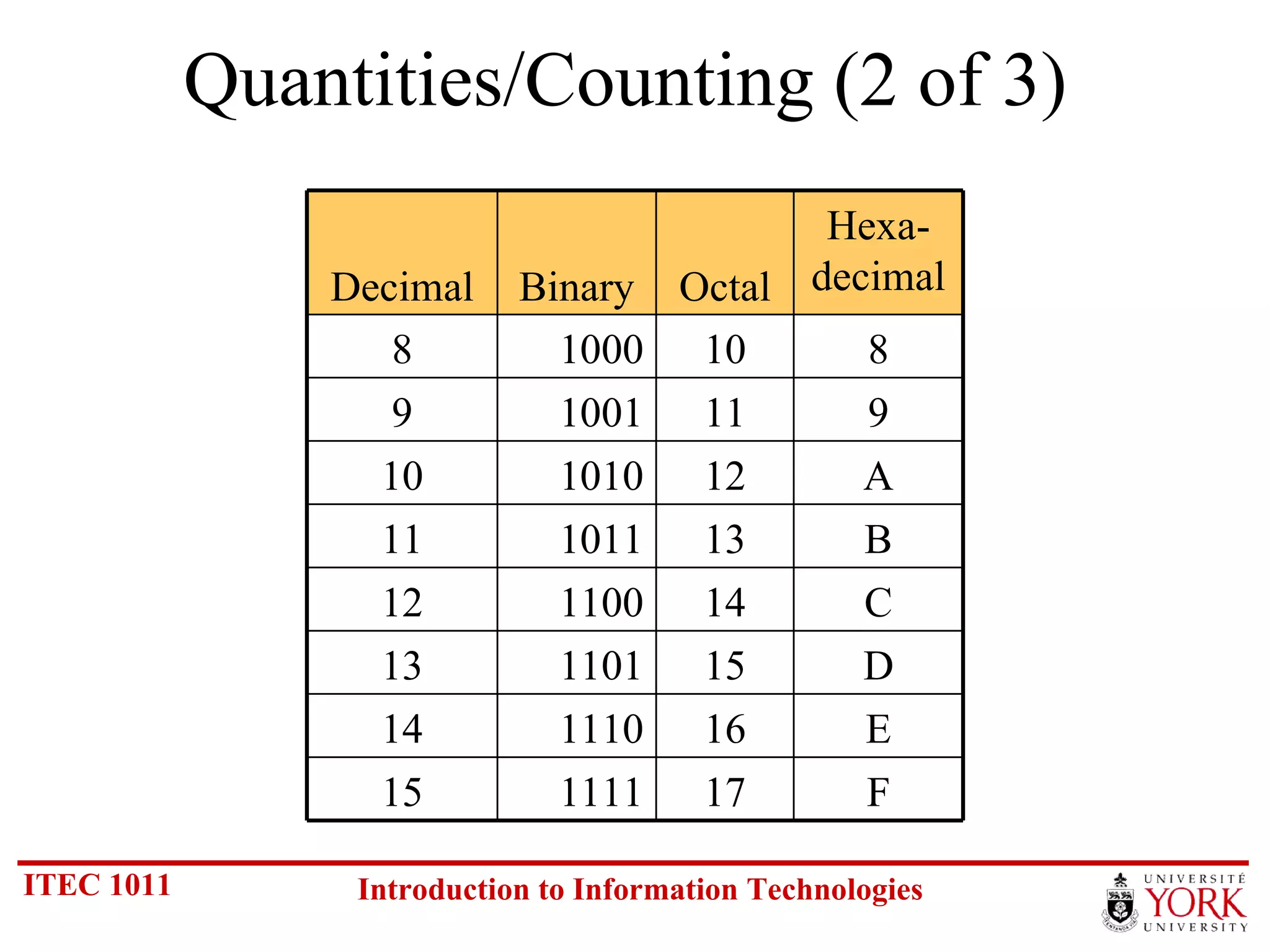
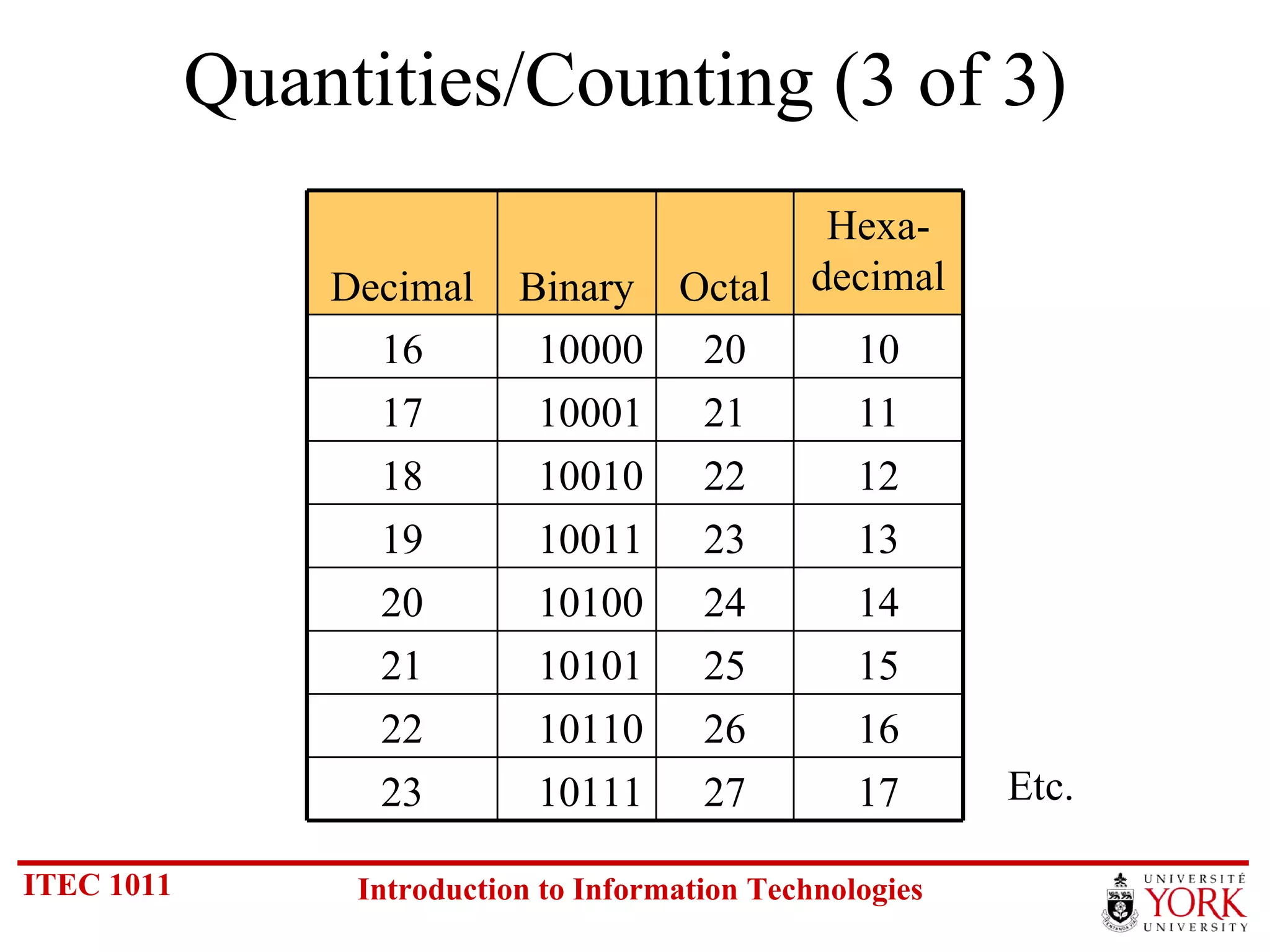
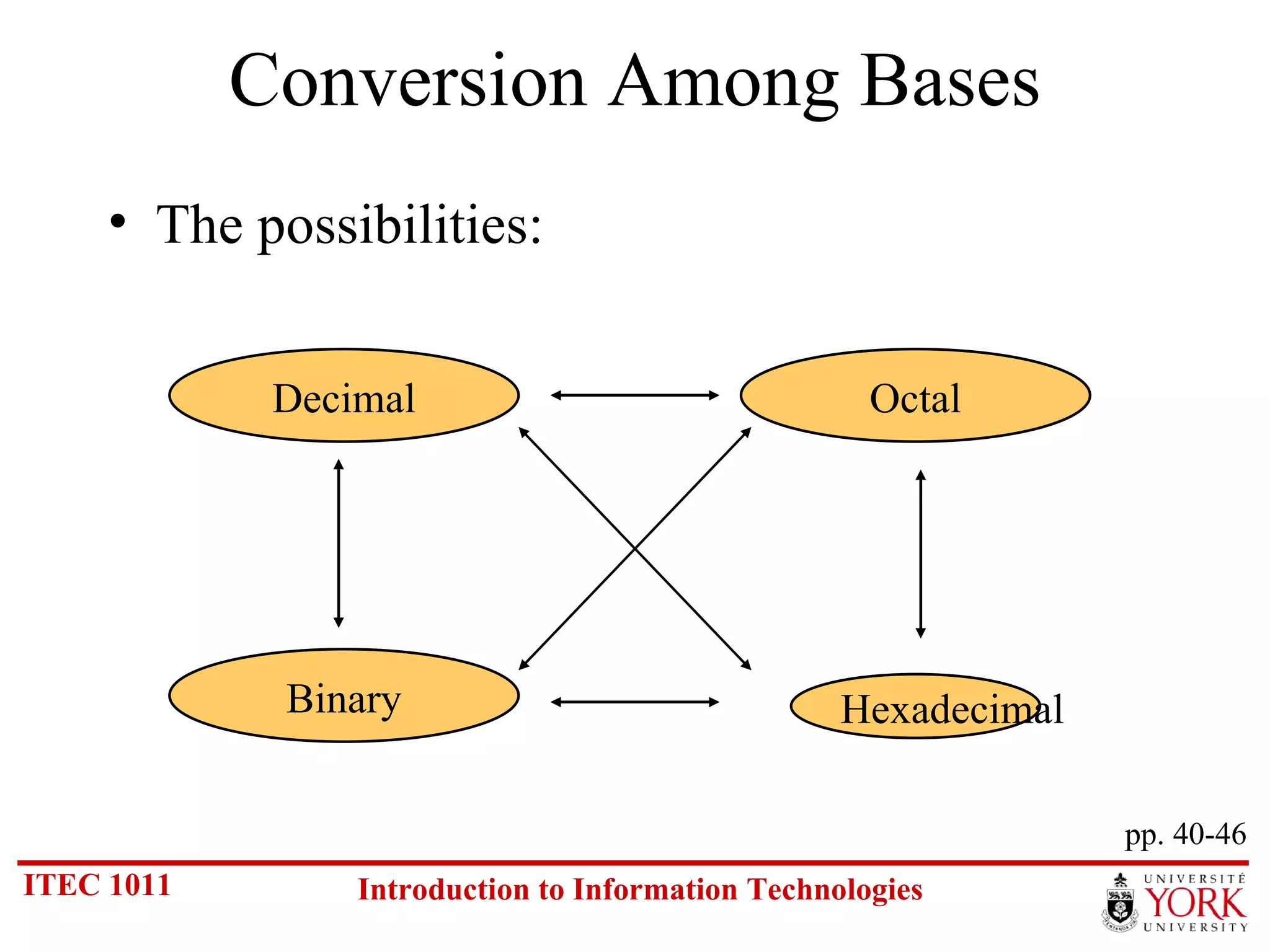
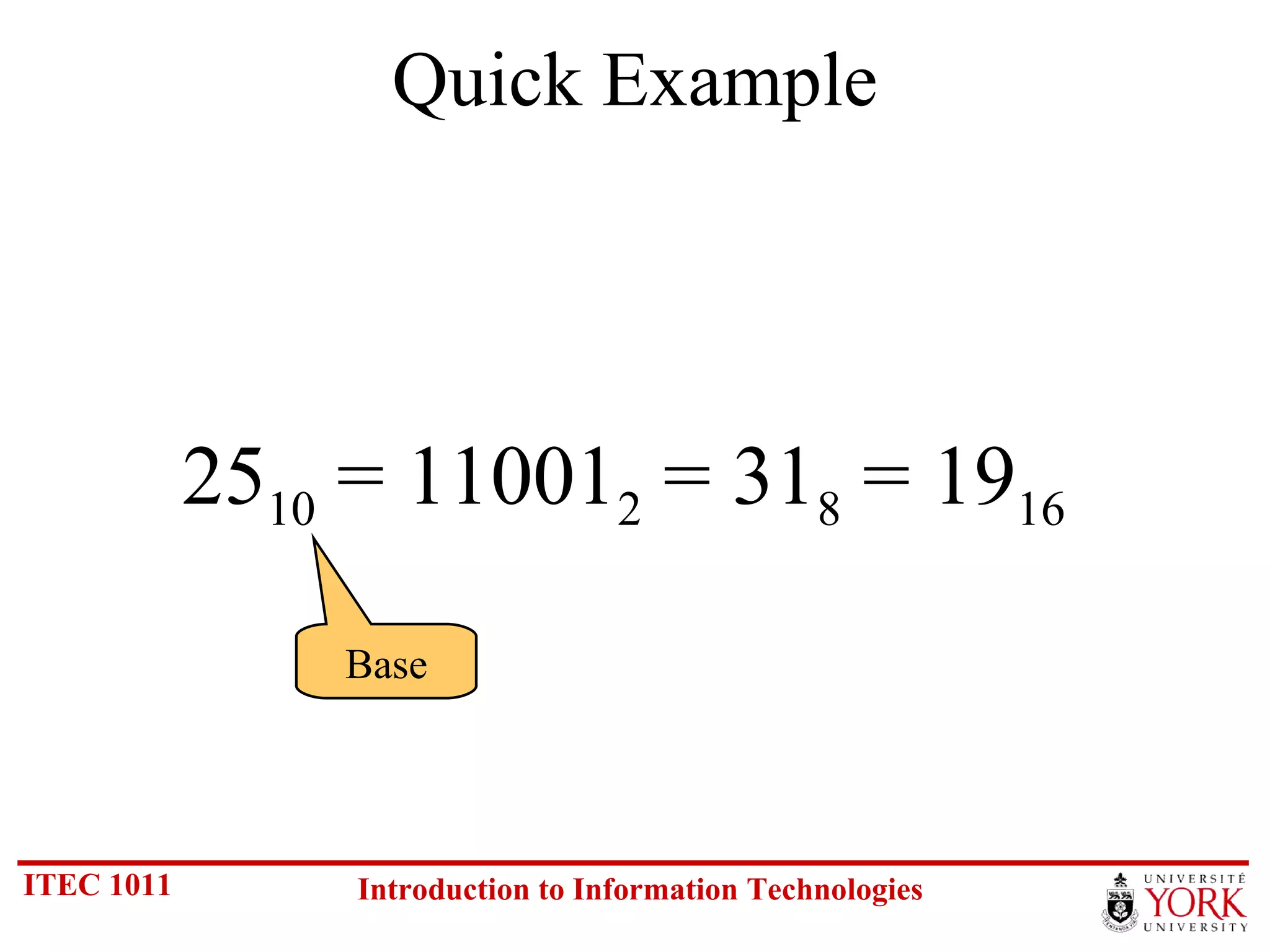
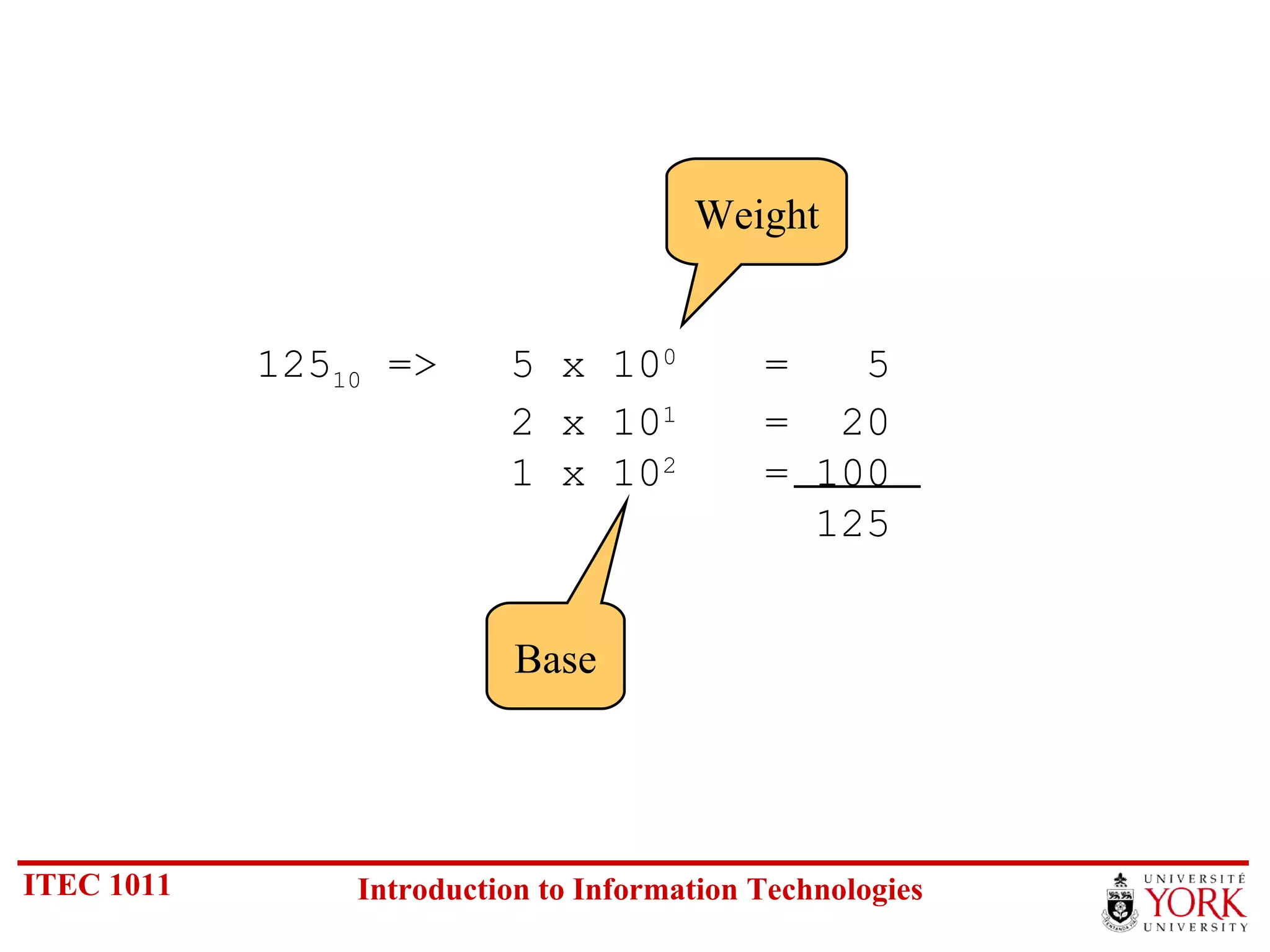
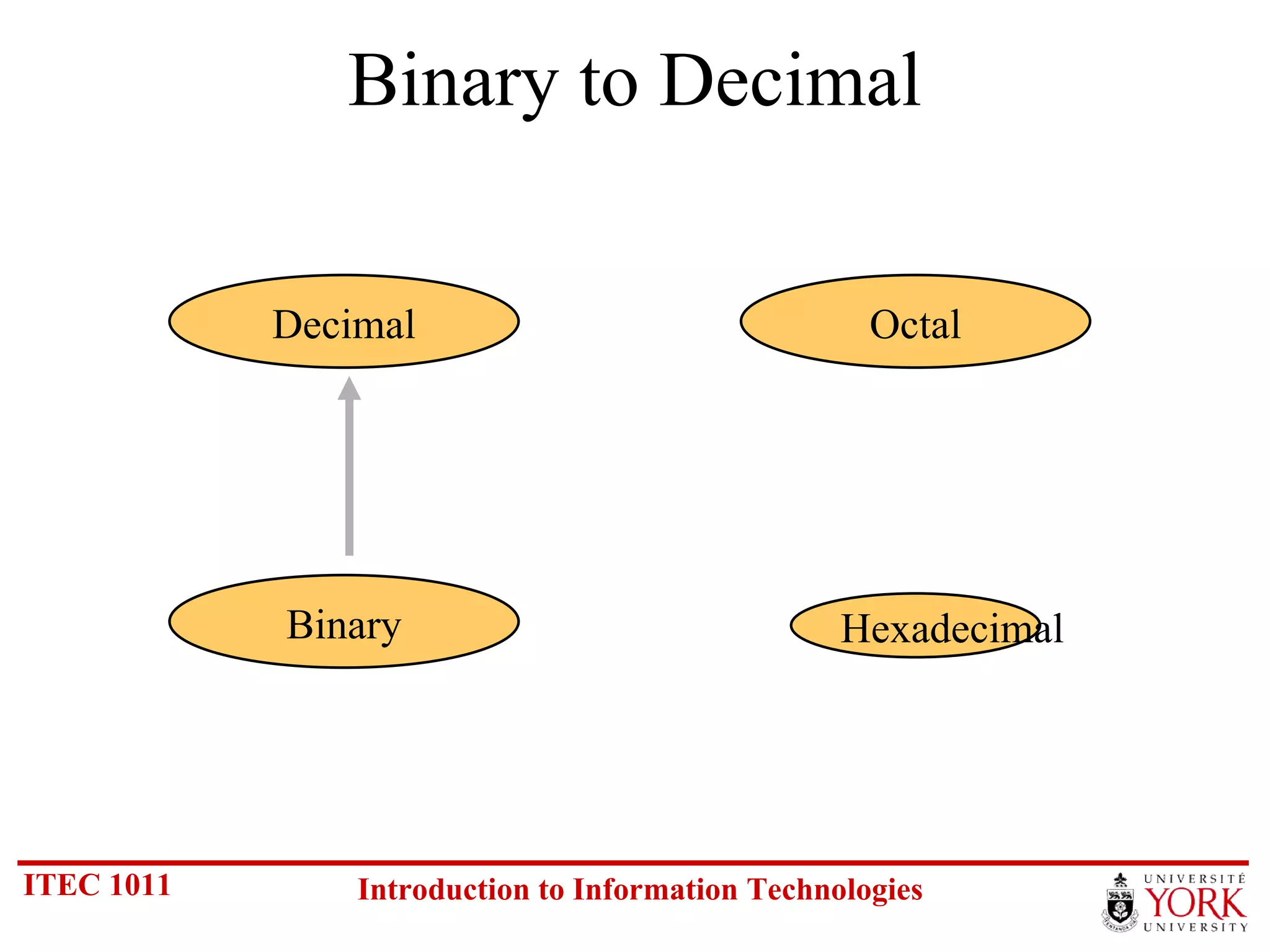
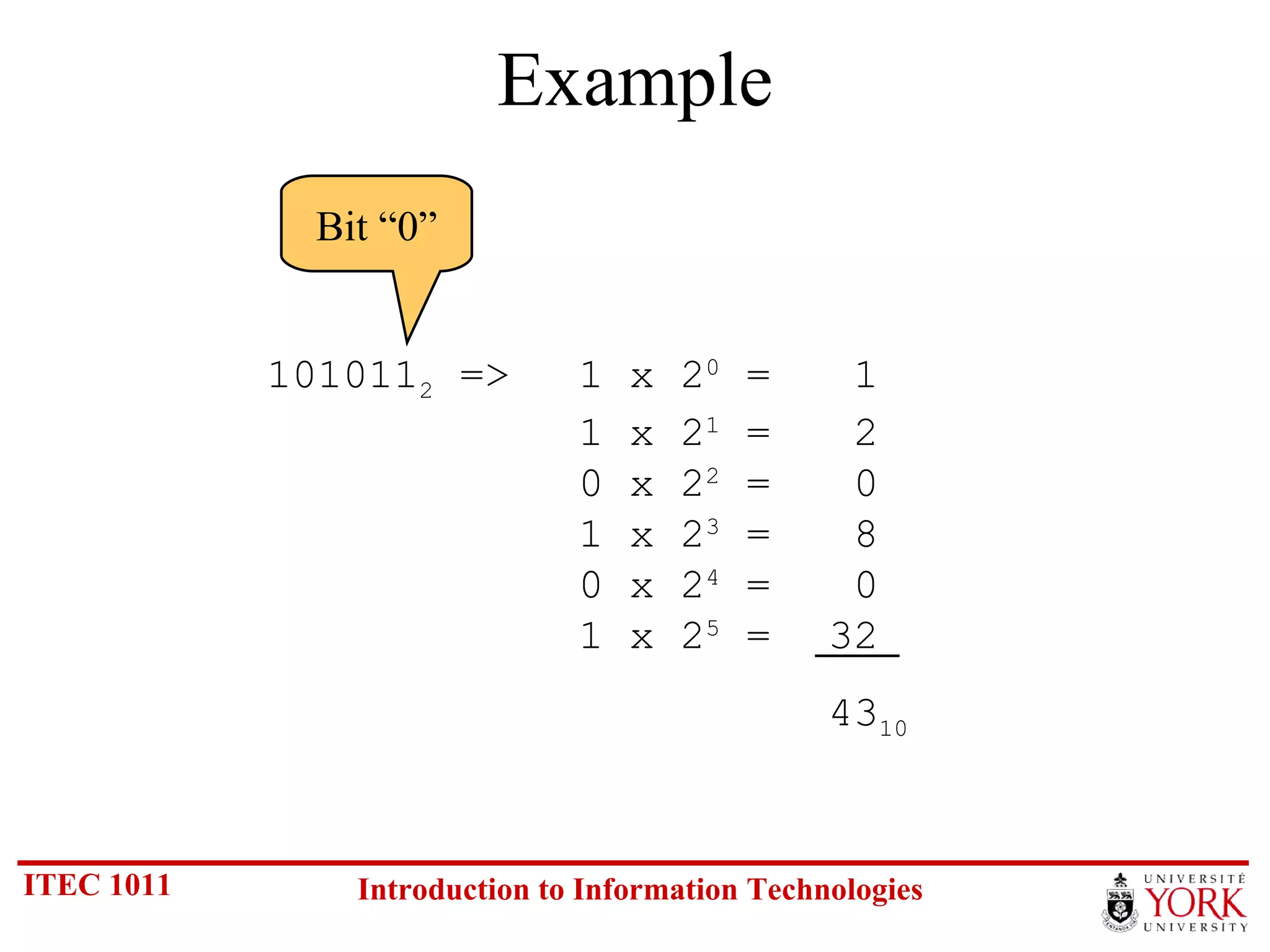
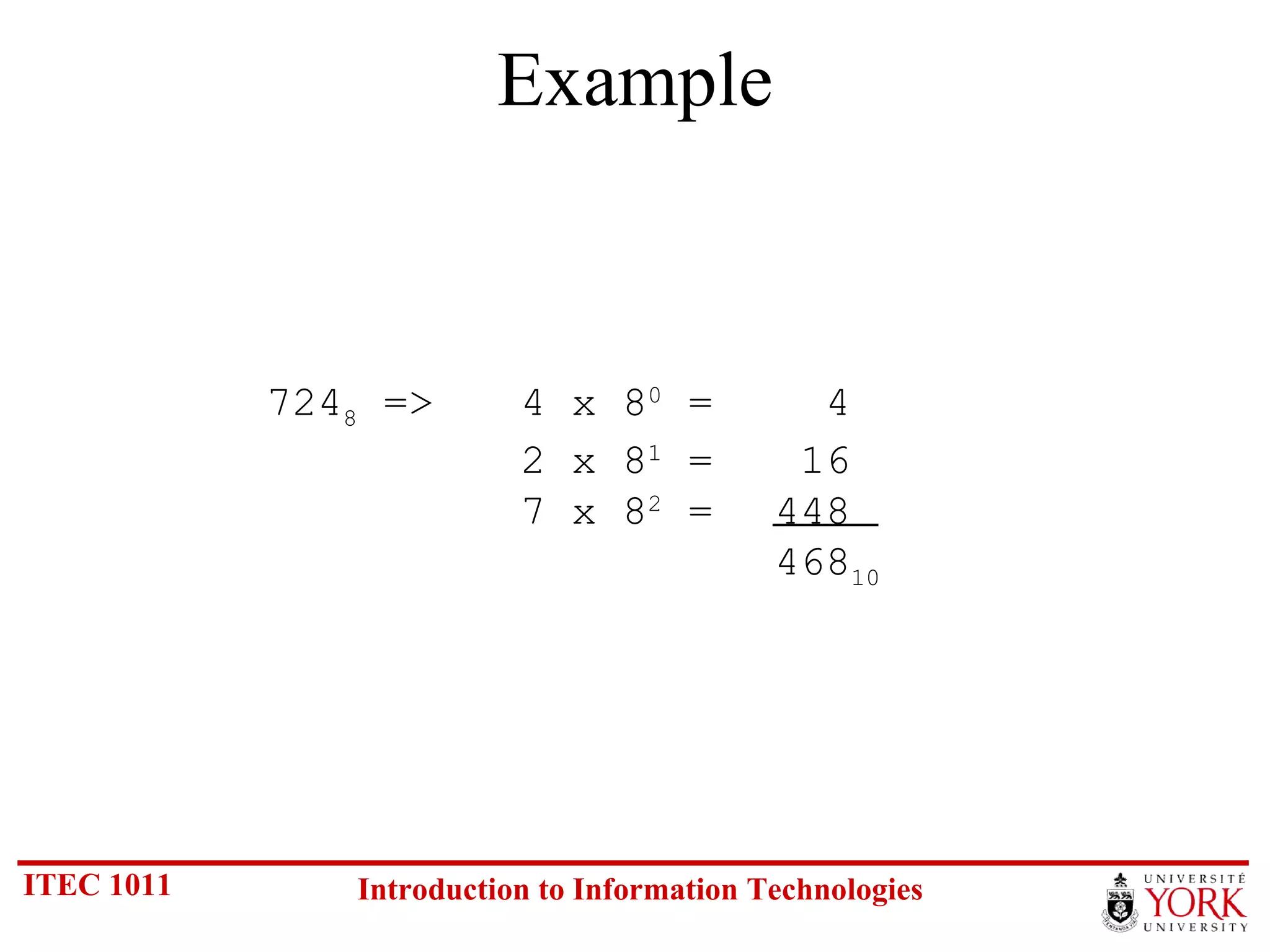
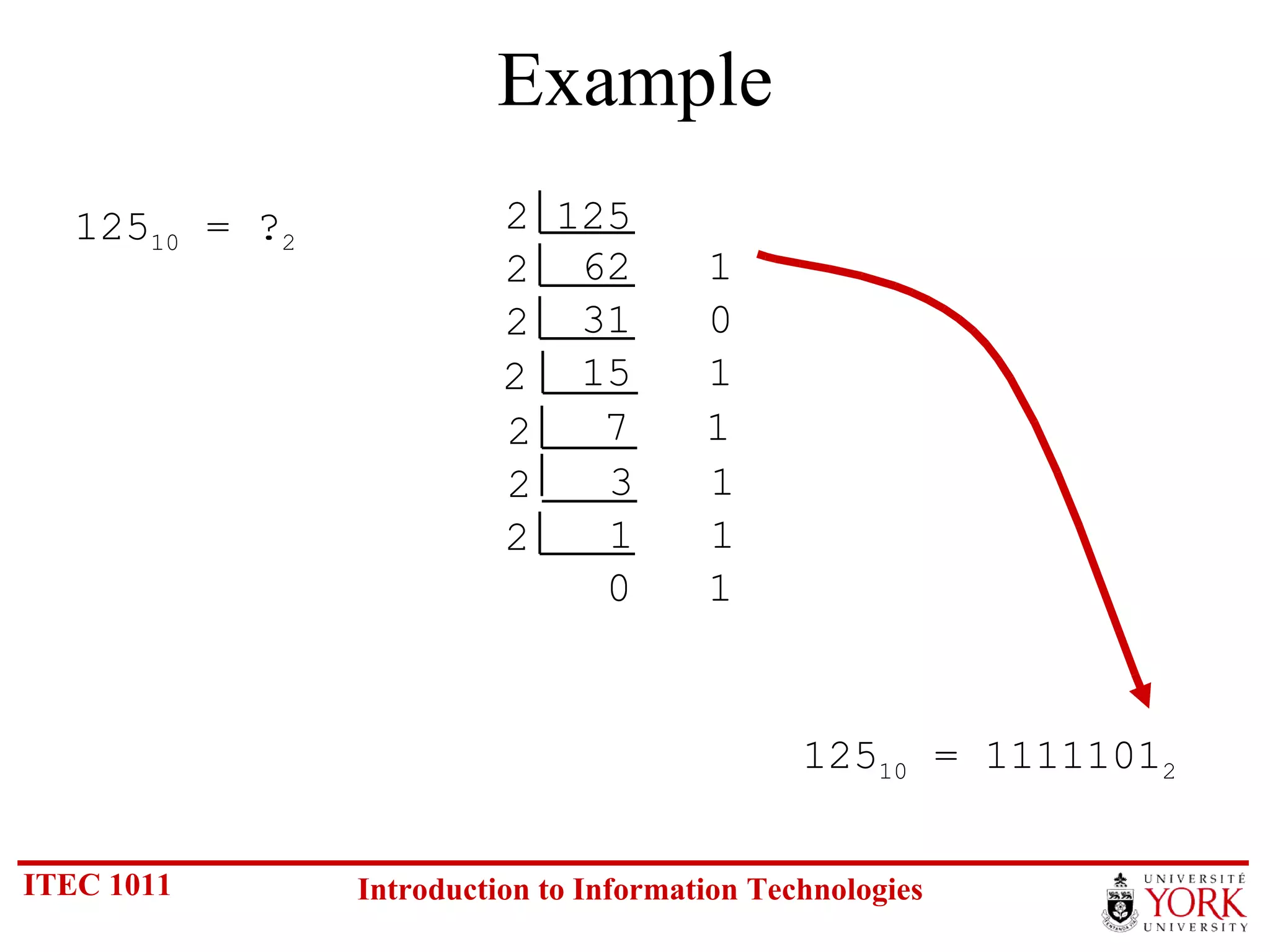
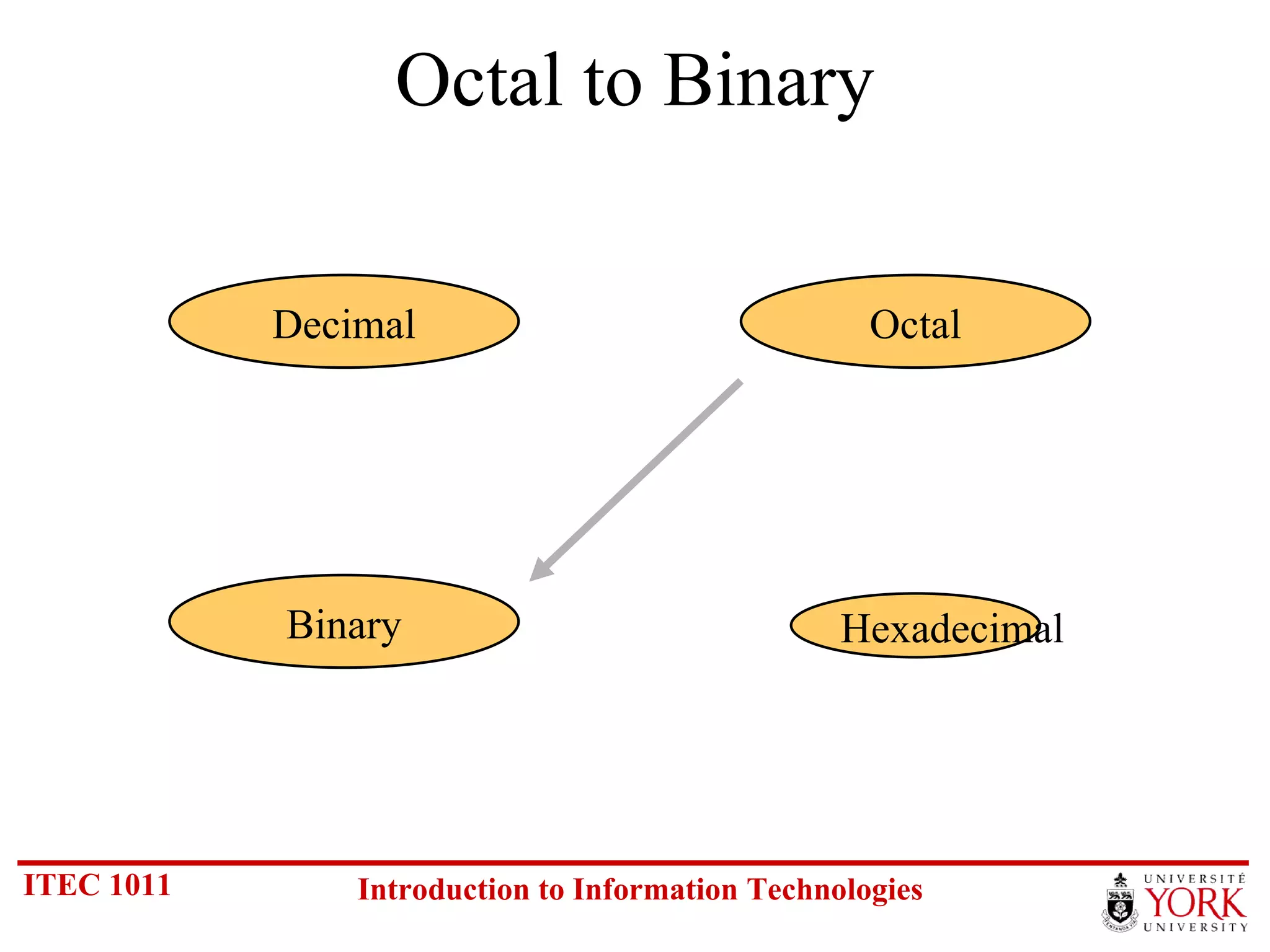
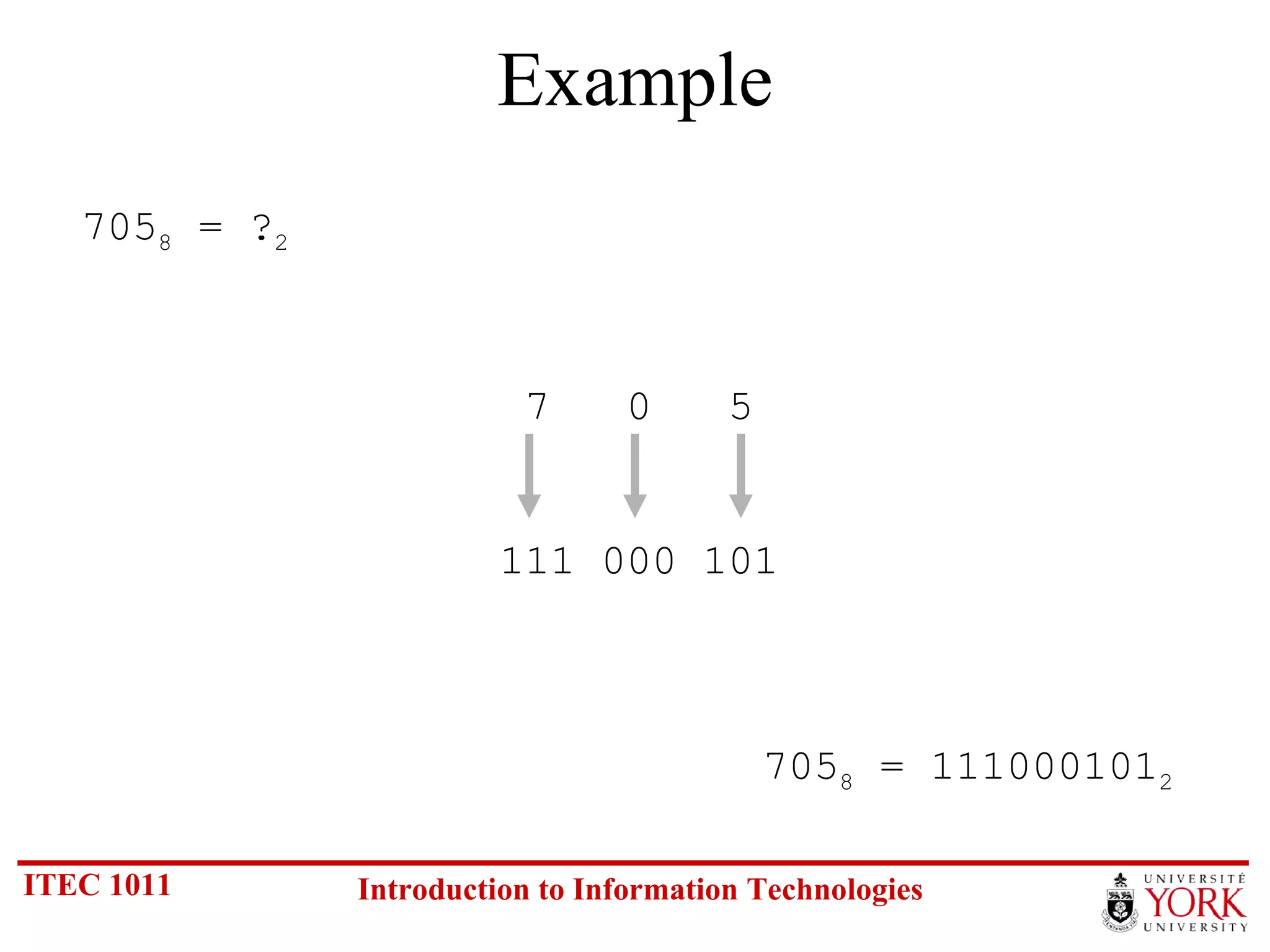
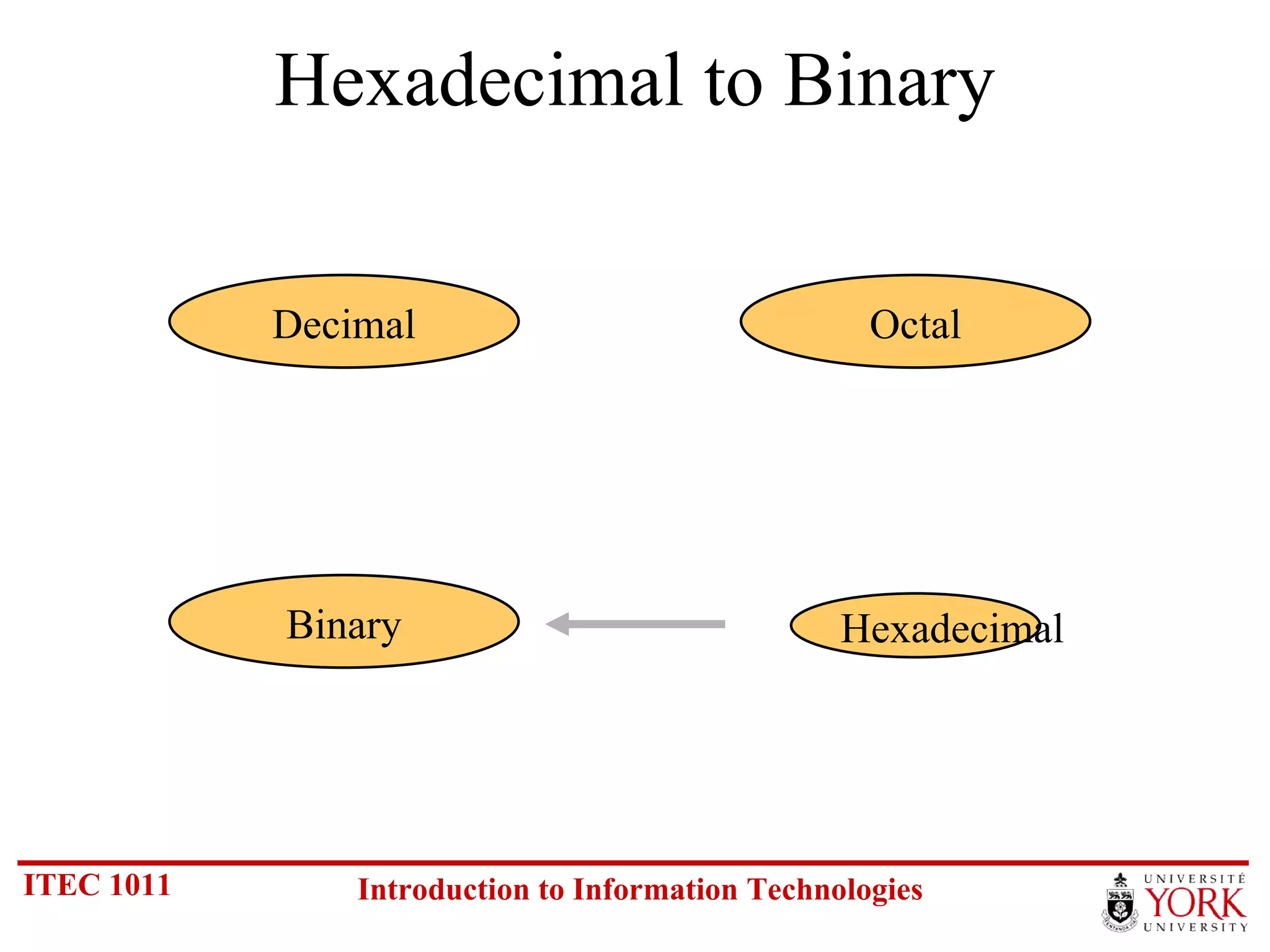
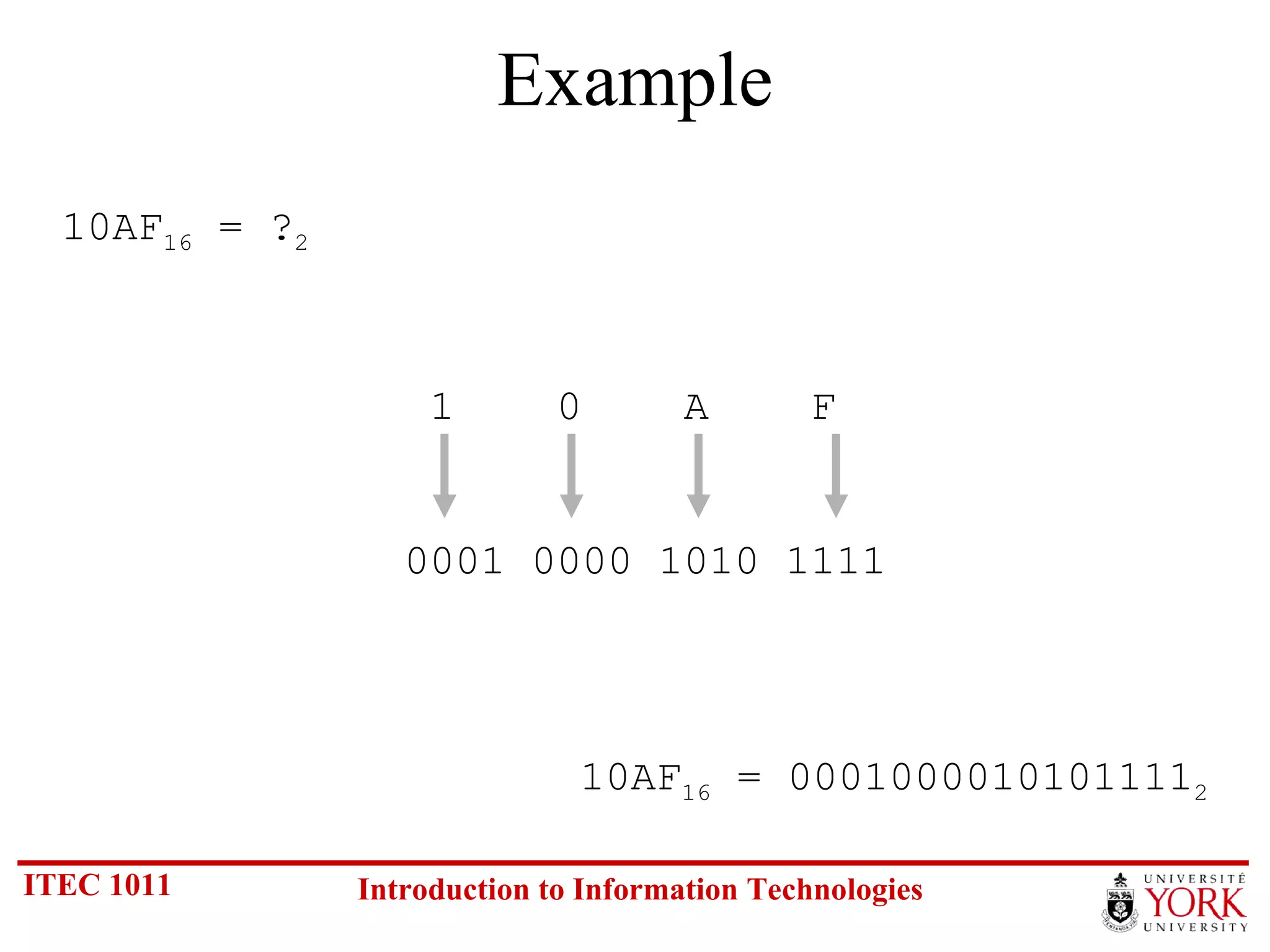
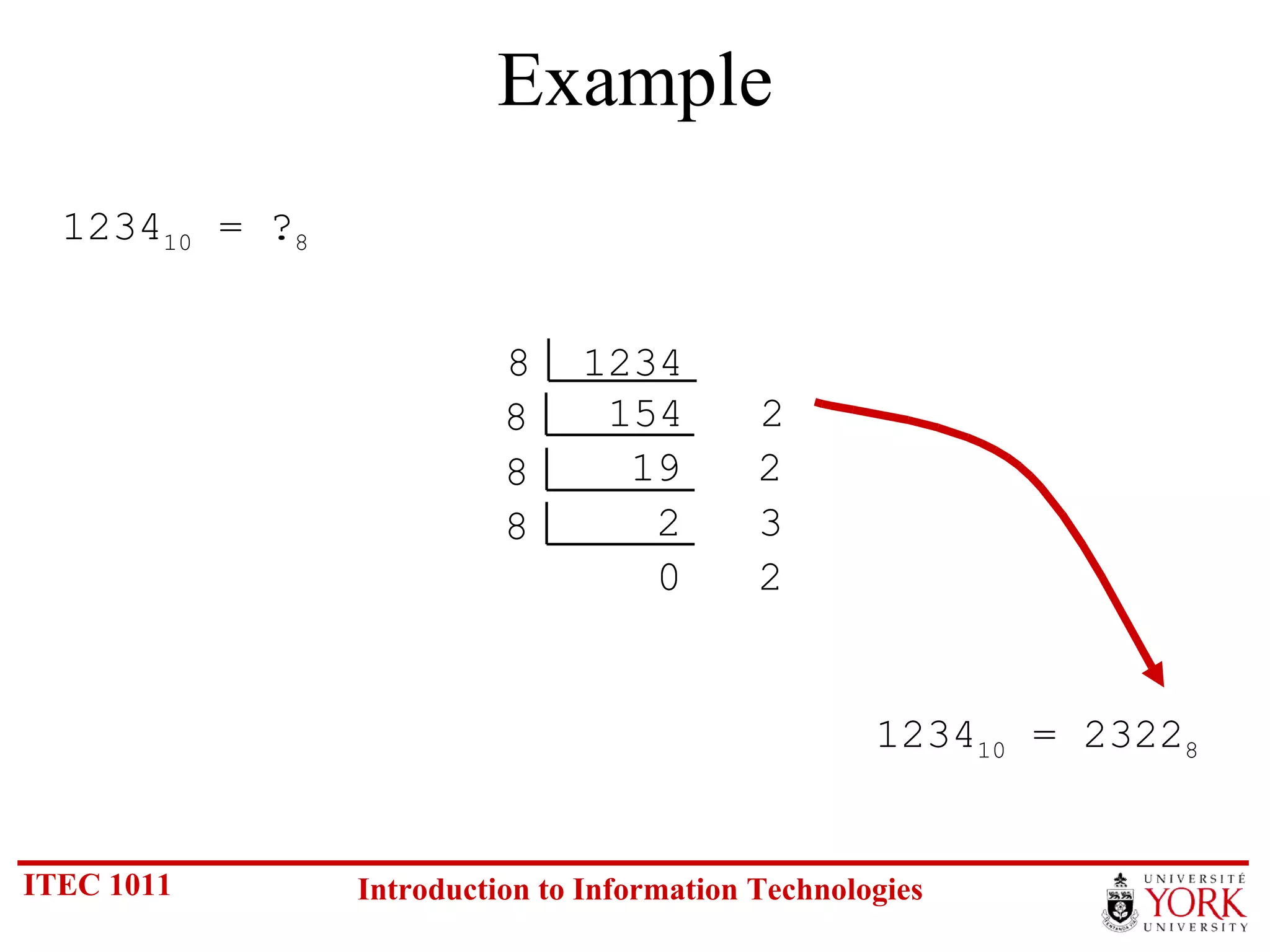
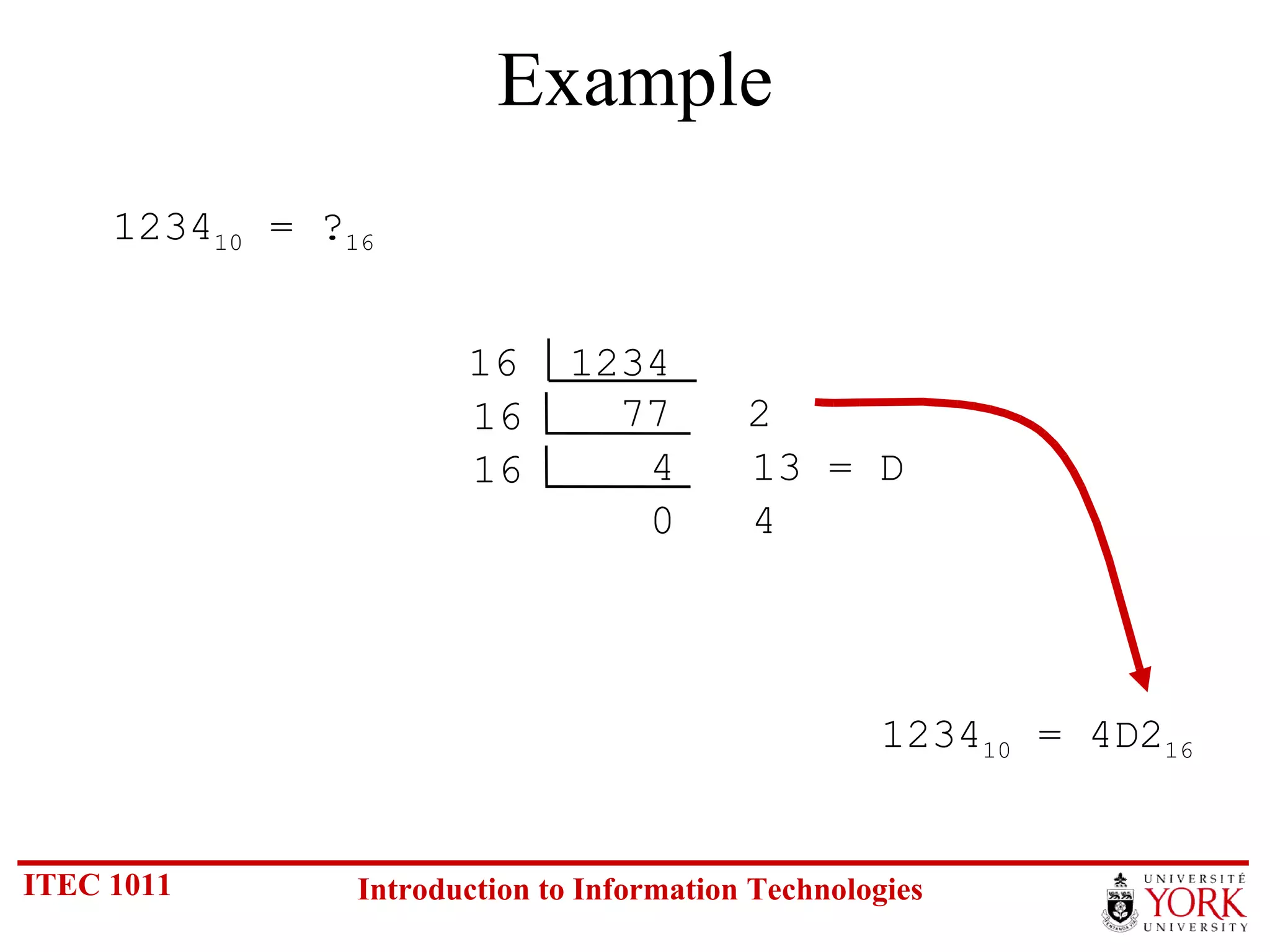
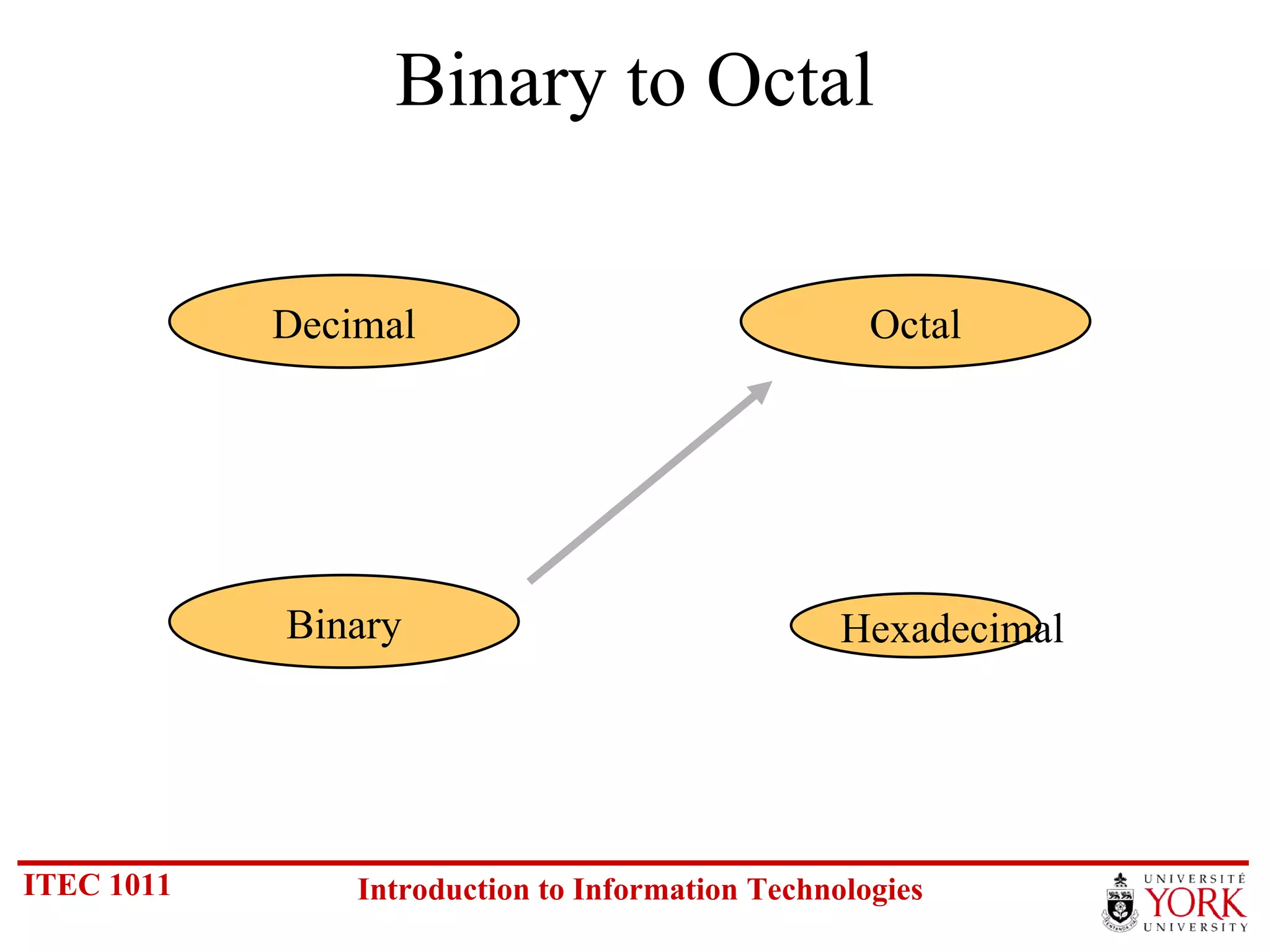
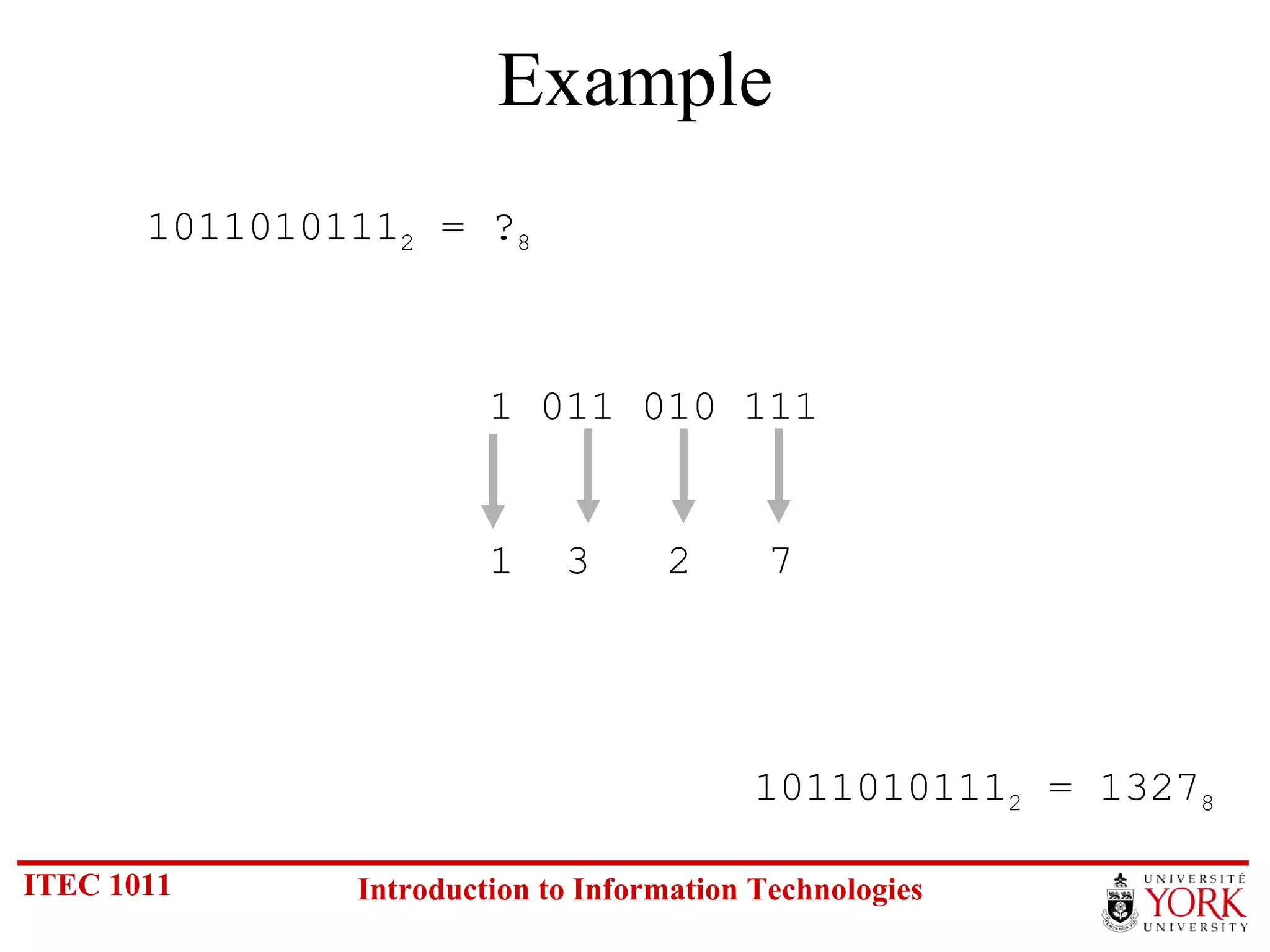
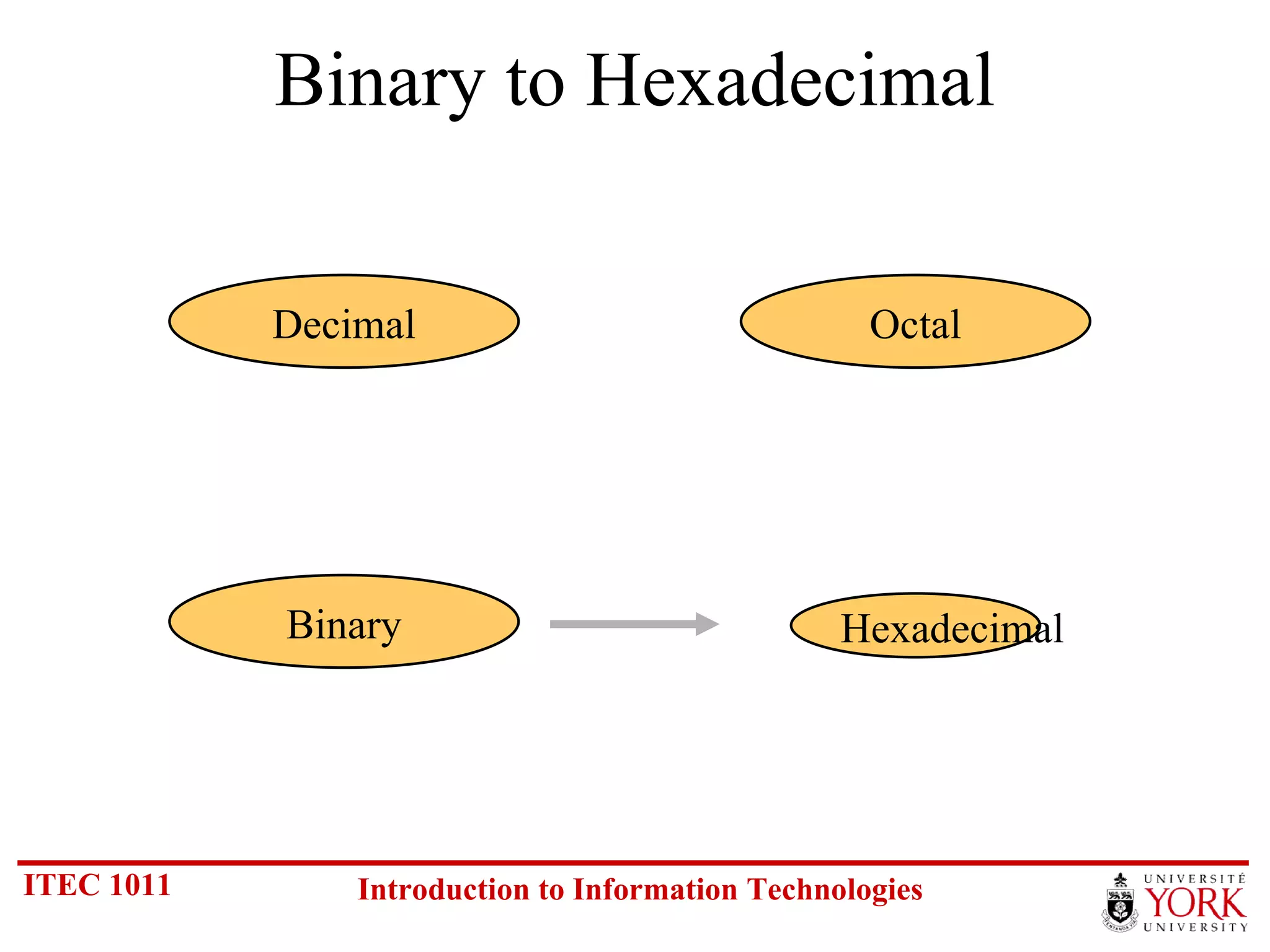
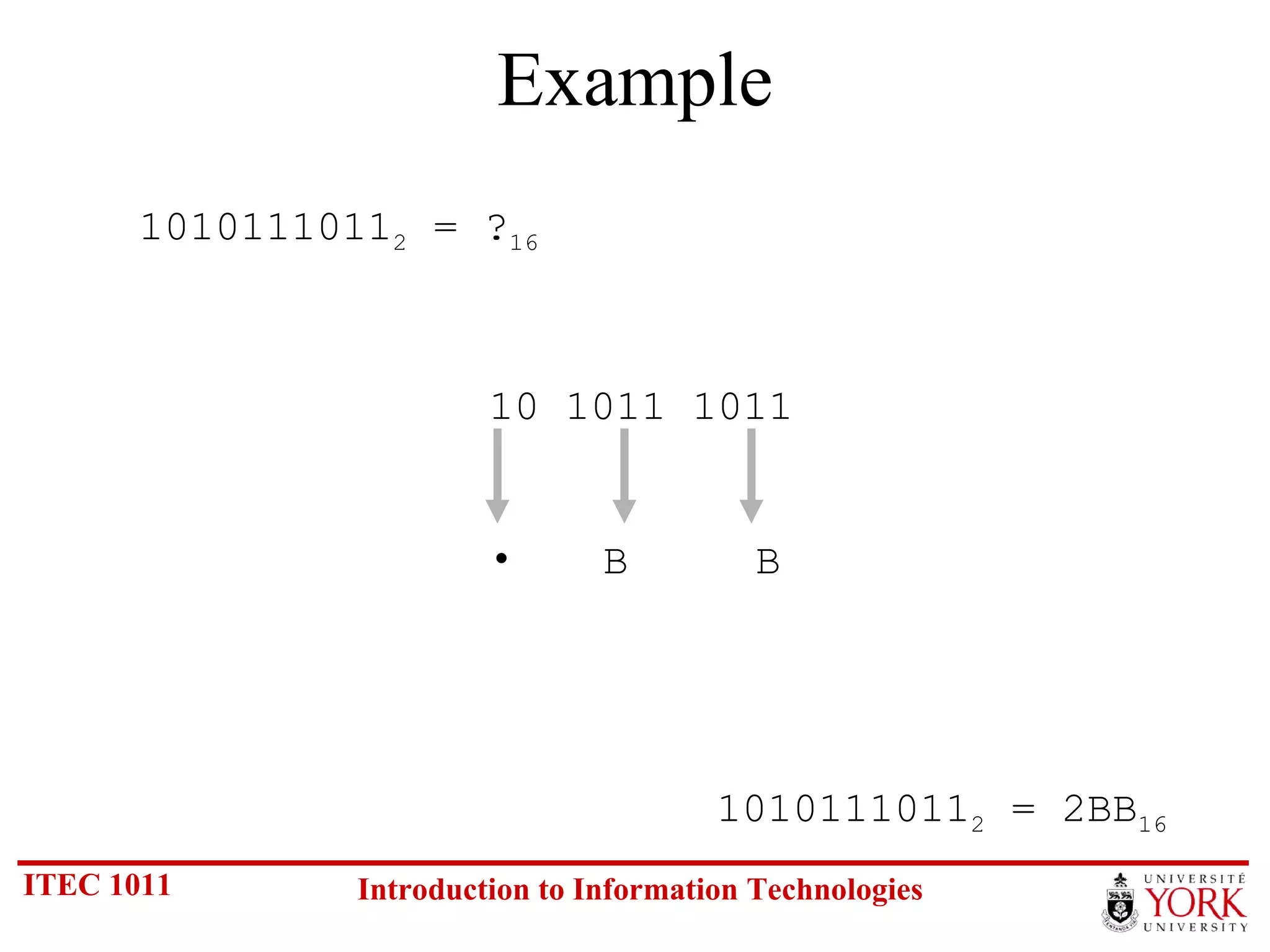
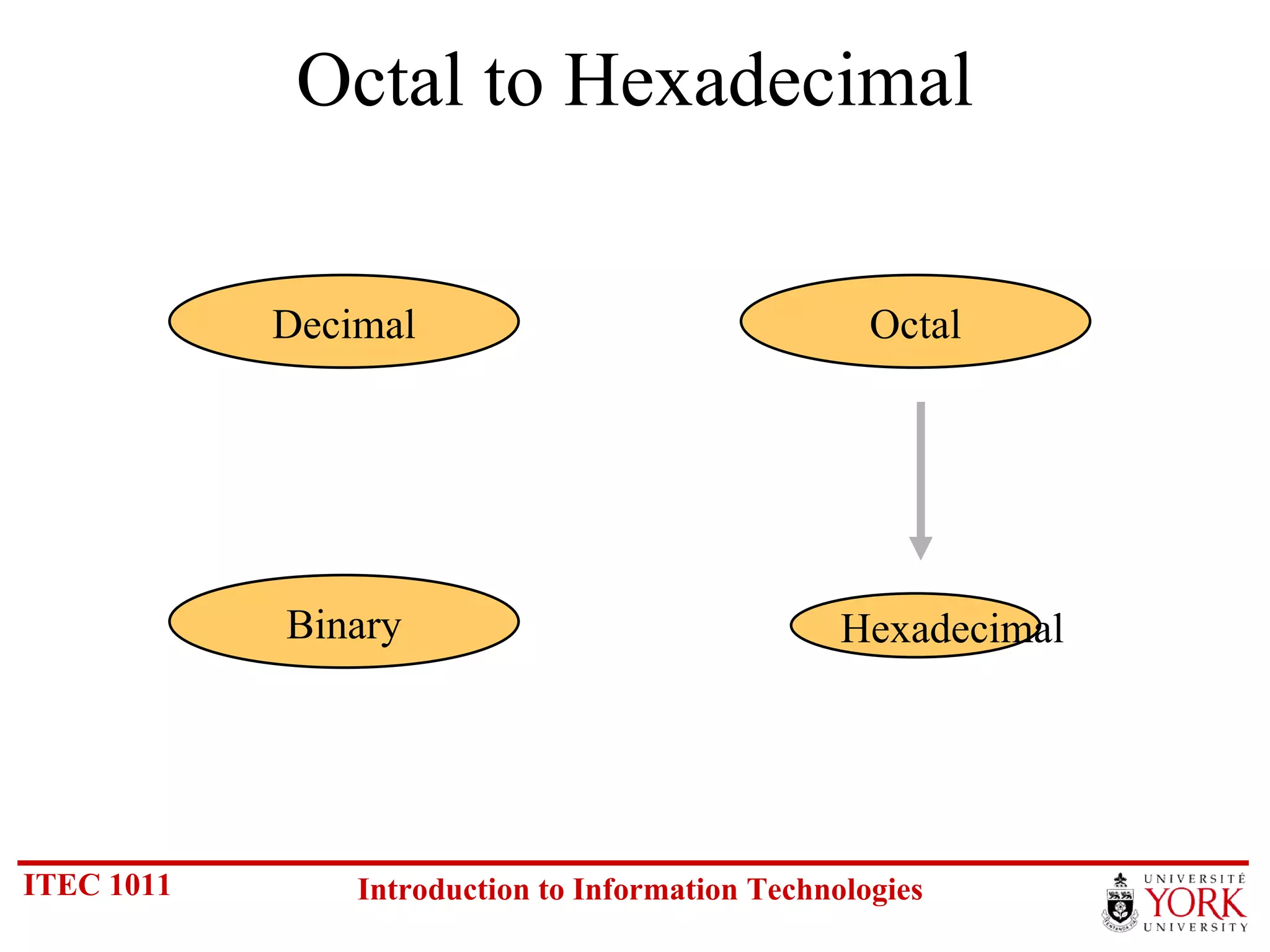
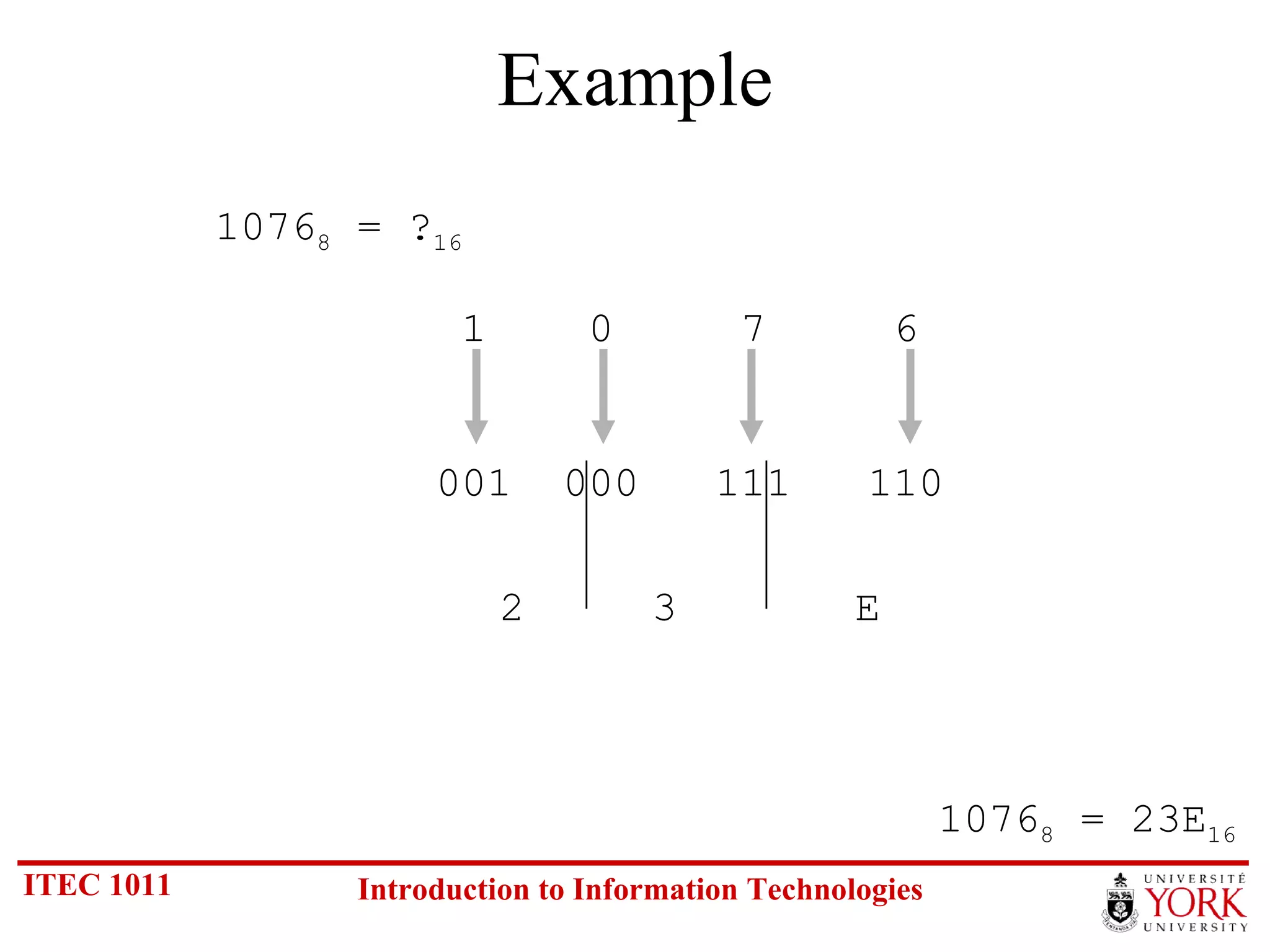
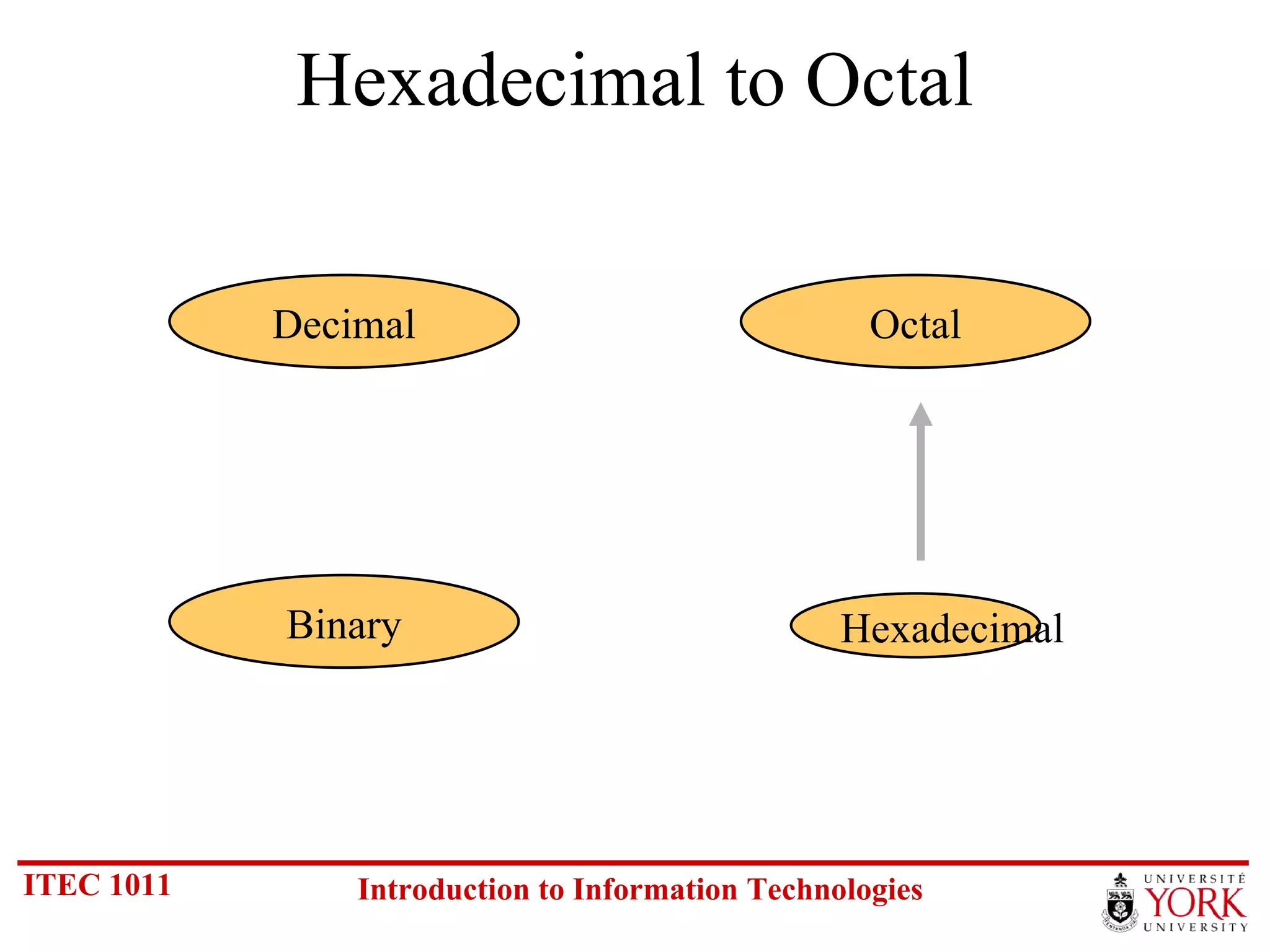
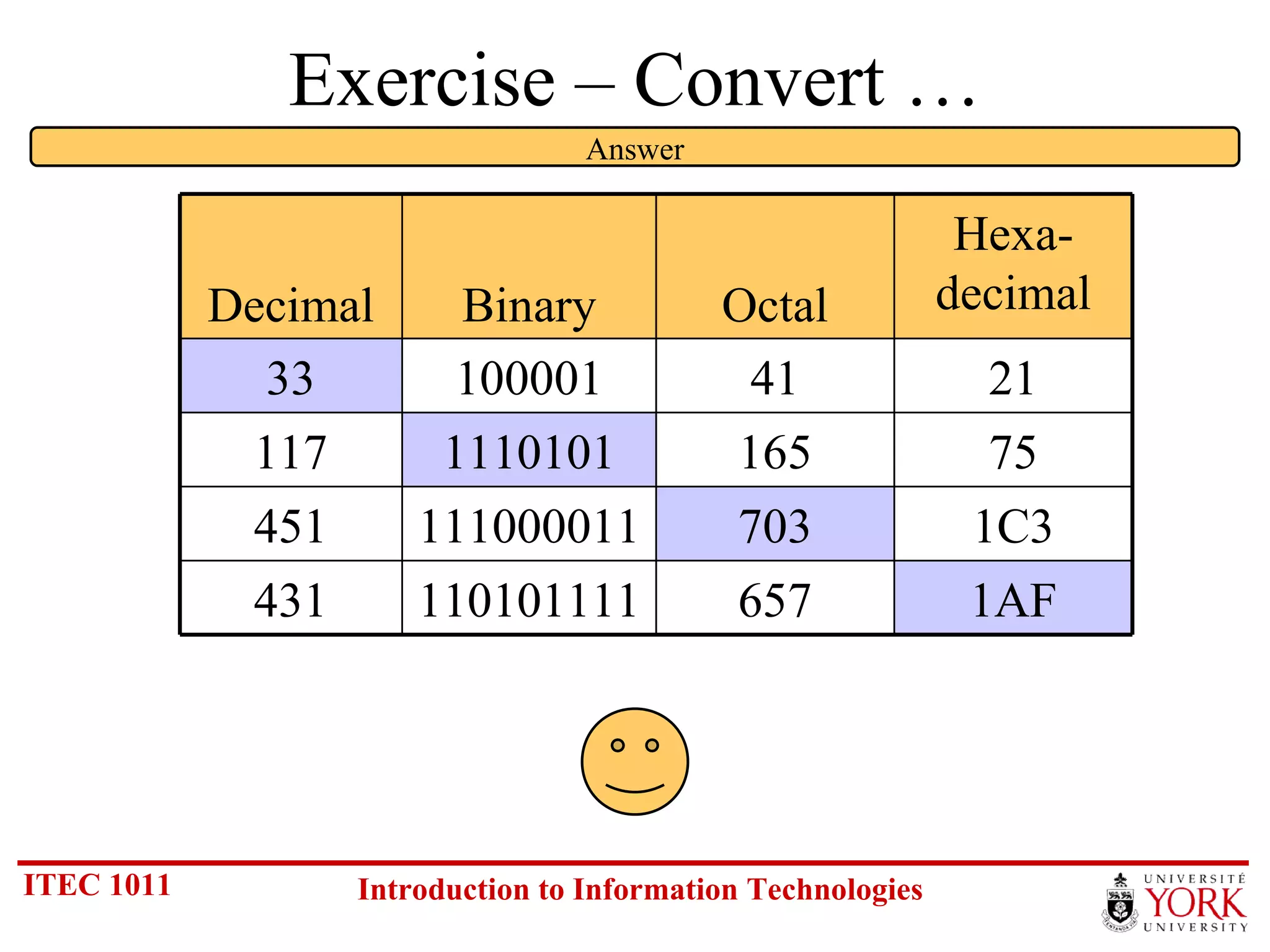
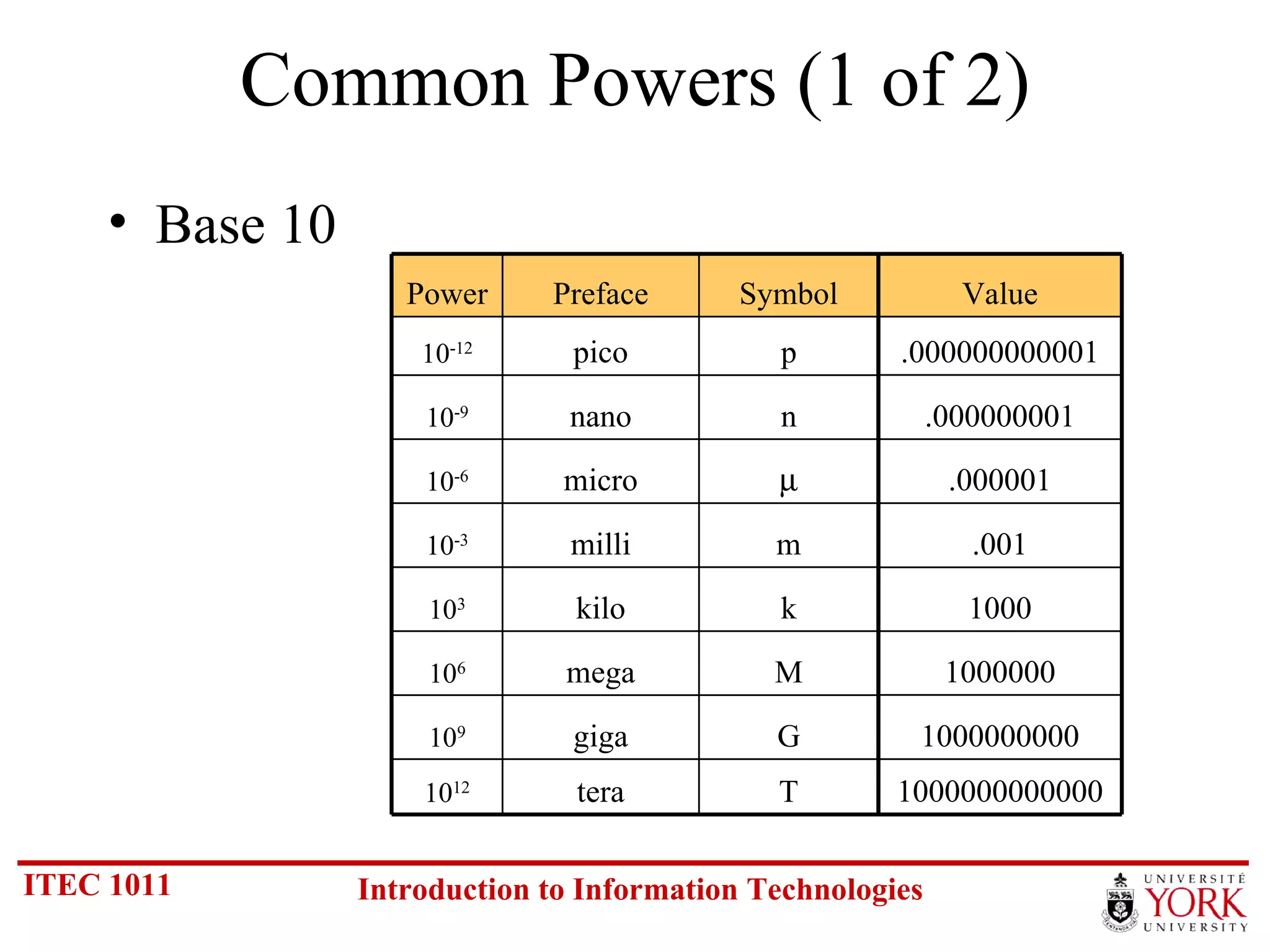
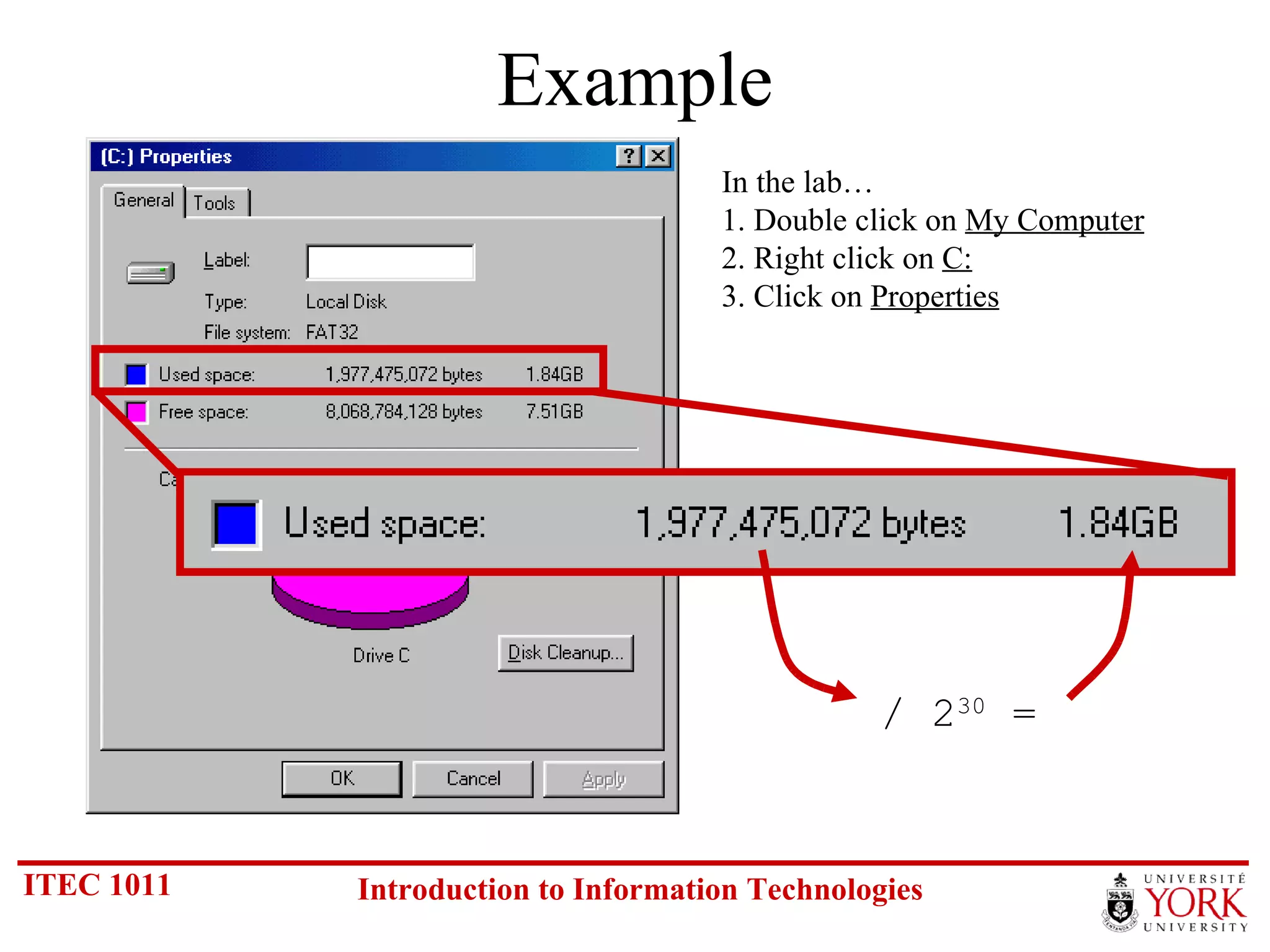
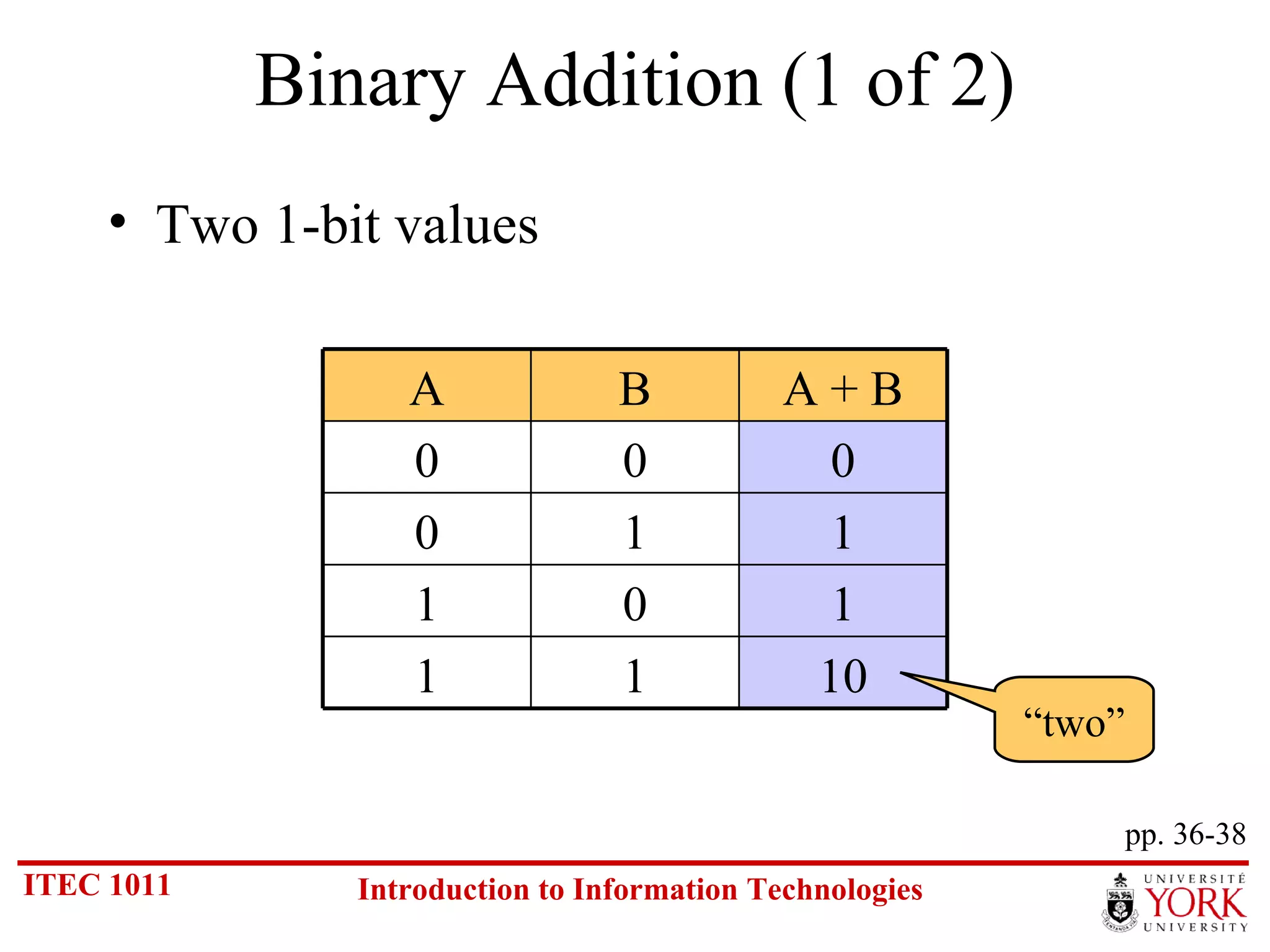
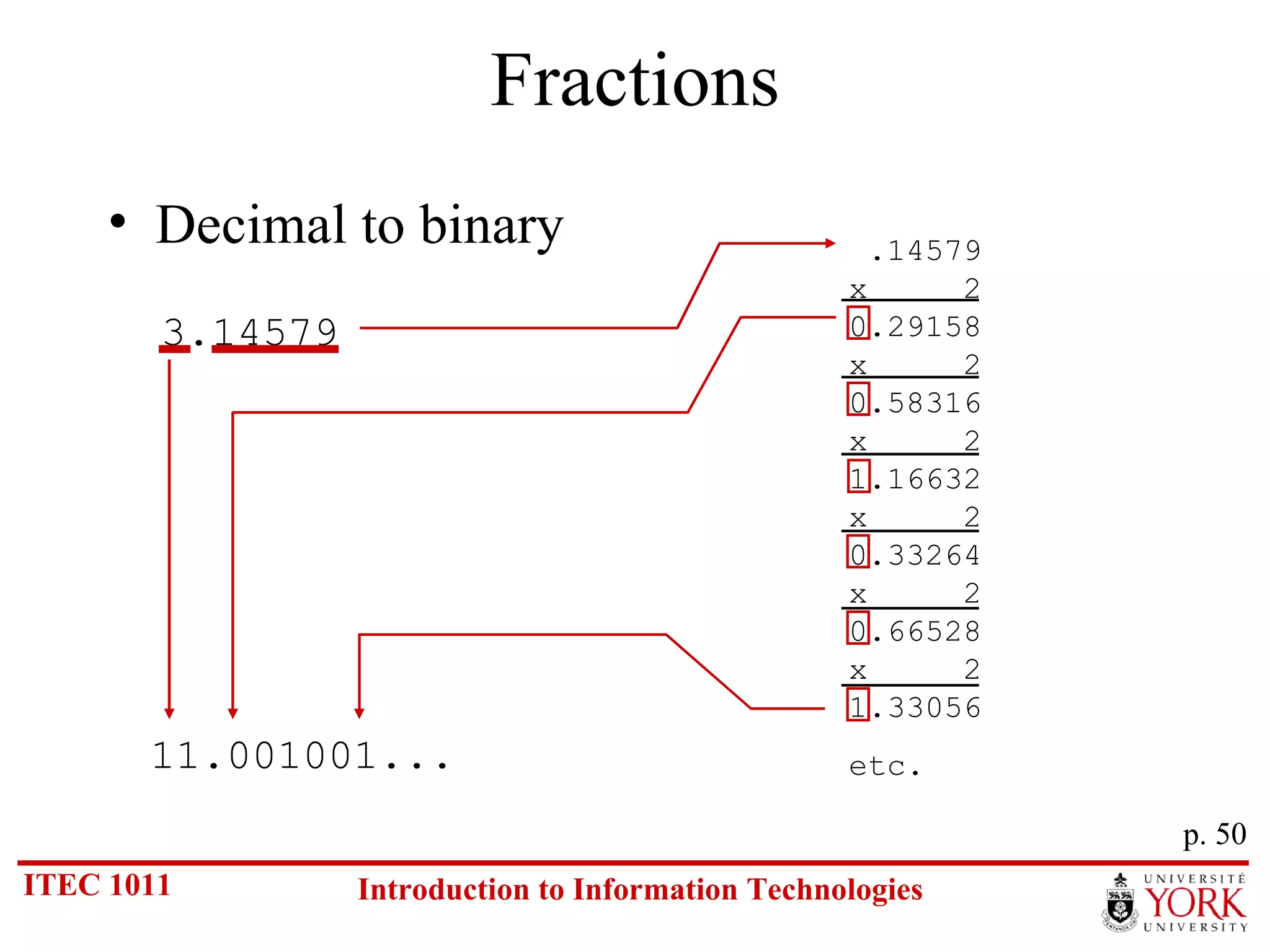
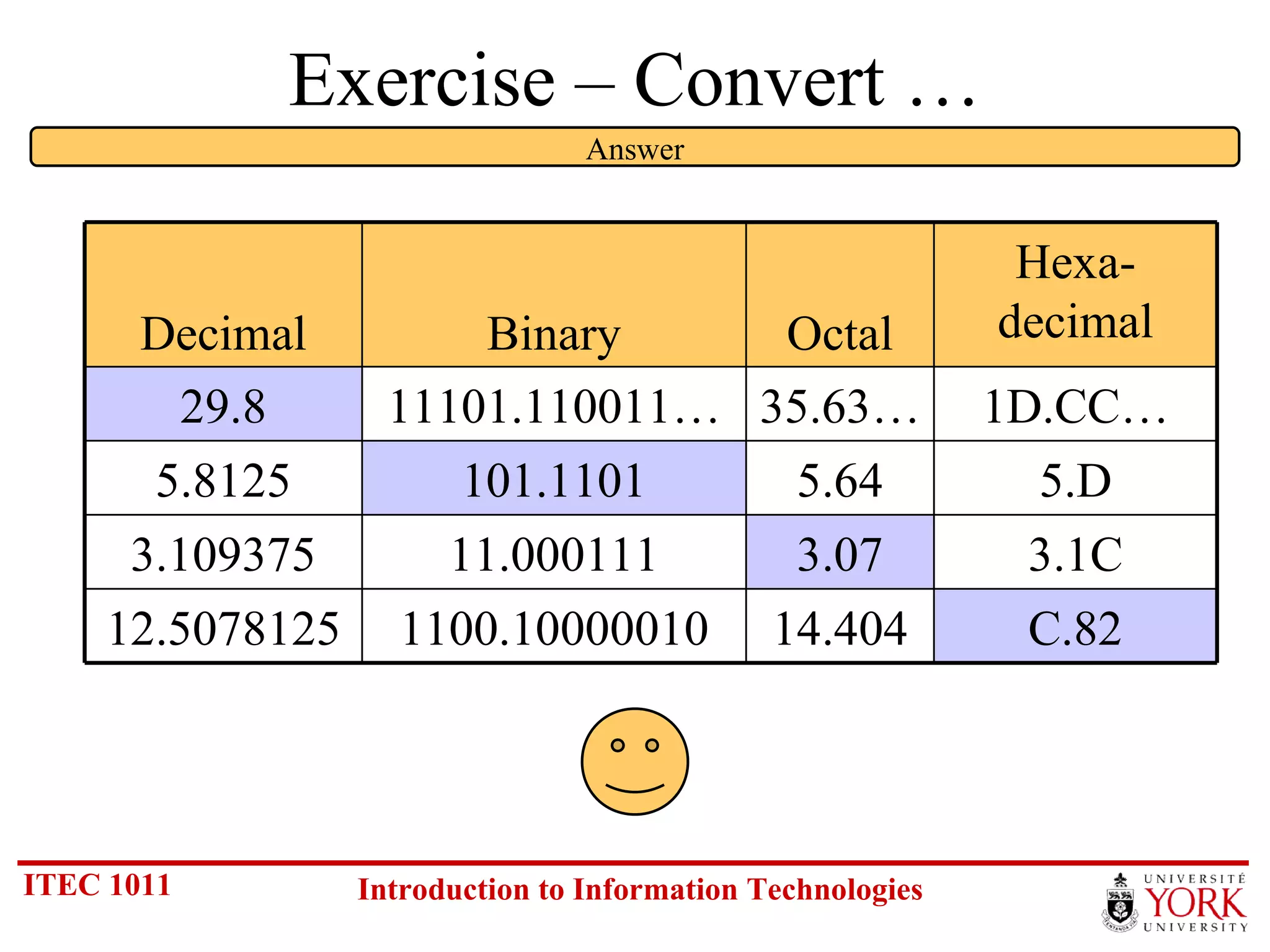
The document discusses various number systems including binary, decimal, octal and hexadecimal. It covers how to convert between these number systems using techniques like dividing by the base, tracking remainders, and grouping bits. Examples are provided for converting between the different systems. Common number prefixes like kilo, mega and giga are also explained in the context of computing.

1. 1. Number Systems Chapt. 2 Location in course textbook

2. Common Number Systems No No 0, 1, … 9, A, B, … F 16 Hexa- decimal No No 0, 1, … 7 8 Octal Yes No 0, 1 2 Binary No Yes 0, 1, … 9 10 Decimal Used in computers? Used by humans? Symbols Base System

3. Quantities/Counting (1 of 3) p. 33 7 7 111 7 6 6 110 6 5 5 101 5 4 4 100 4 3 3 11 3 2 2 10 2 1 1 1 1 0 0 0 0 Hexa- decimal Octal Binary Decimal

4. Quantities/Counting (2 of 3) F 17 1111 15 E 16 1110 14 D 15 1101 13 C 14 1100 12 B 13 1011 11 A 12 1010 10 9 11 1001 9 8 10 1000 8 Hexa- decimal Octal Binary Decimal

5. Quantities/Counting (3 of 3) Etc. 17 27 10111 23 16 26 10110 22 15 25 10101 21 14 24 10100 20 13 23 10011 19 12 22 10010 18 11 21 10001 17 10 20 10000 16 Hexa- decimal Octal Binary Decimal

6. Conversion Among Bases The possibilities: Hexadecimal Decimal Octal Binary pp. 40-46

7. Quick Example 25 10 = 11001 2 = 31 8 = 19 16 Base

8. Decimal to Decimal (just for fun) Hexadecimal Decimal Octal Binary Next slide…

9. 125 10 => 5 x 10 0 = 5 2 x 10 1 = 20 1 x 10 2 = 100 125 Base Weight

10. Binary to Decimal Hexadecimal Decimal Octal Binary

11. Binary to Decimal Technique Multiply each bit by 2 n , where n is the “weight” of the bit The weight is the position of the bit, starting from 0 on the right Add the results

12. Example 101011 2 => 1 x 2 0 = 1 1 x 2 1 = 2 0 x 2 2 = 0 1 x 2 3 = 8 0 x 2 4 = 0 1 x 2 5 = 32 43 10 Bit “0”

13. Octal to Decimal Hexadecimal Decimal Octal Binary

14. Octal to Decimal Technique Multiply each bit by 8 n , where n is the “weight” of the bit The weight is the position of the bit, starting from 0 on the right Add the results

15. Example 724 8 => 4 x 8 0 = 4 2 x 8 1 = 16 7 x 8 2 = 448 468 10

16. Hexadecimal to Decimal Hexadecimal Decimal Octal Binary

17. Hexadecimal to Decimal Technique Multiply each bit by 16 n , where n is the “weight” of the bit The weight is the position of the bit, starting from 0 on the right Add the results

18. Example ABC 16 => C x 16 0 = 12 x 1 = 12 B x 16 1 = 11 x 16 = 176 A x 16 2 = 10 x 256 = 2560 2748 10

19. Decimal to Binary Hexadecimal Decimal Octal Binary

20. Decimal to Binary Technique Divide by two, keep track of the remainder First remainder is bit 0 (LSB, least-significant bit) Second remainder is bit 1 Etc.

21. Example 125 10 = ? 2 125 10 = 1111101 2 2 125 62 1 2 31 0 2 15 1 2 7 1 2 3 1 2 1 1 2 0 1

22. Octal to Binary Hexadecimal Decimal Octal Binary

23. Octal to Binary Technique Convert each octal digit to a 3-bit equivalent binary representation

24. Example 705 8 = ? 2 705 8 = 111000101 2 7 0 5 111 000 101

25. Hexadecimal to Binary Hexadecimal Decimal Octal Binary

26. Hexadecimal to Binary Technique Convert each hexadecimal digit to a 4-bit equivalent binary representation

27. Example 10AF 16 = ? 2 10AF 16 = 0001000010101111 2 1 0 A F 0001 0000 1010 1111

28. Decimal to Octal Hexadecimal Decimal Octal Binary

29. Decimal to Octal Technique Divide by 8 Keep track of the remainder

30. Example 1234 10 = ? 8 8 1234 154 2 1234 10 = 2322 8 8 19 2 8 2 3 8 0 2

31. Decimal to Hexadecimal Hexadecimal Decimal Octal Binary

32. Decimal to Hexadecimal Technique Divide by 16 Keep track of the remainder

33. Example 1234 10 = ? 16 1234 10 = 4D2 16 16 1234 77 2 16 4 13 = D 16 0 4

34. Binary to Octal Hexadecimal Decimal Octal Binary

35. Binary to Octal Technique Group bits in threes, starting on right Convert to octal digits

36. Example 1011010111 2 = ? 8 1011010111 2 = 1327 8 1 011 010 111 1 3 2 7

37. Binary to Hexadecimal Hexadecimal Decimal Octal Binary

38. Binary to Hexadecimal Technique Group bits in fours, starting on right Convert to hexadecimal digits

39. Example 1010111011 2 = ? 16 10 1011 1011 B B 1010111011 2 = 2BB 16

40. Octal to Hexadecimal Hexadecimal Decimal Octal Binary

41. Octal to Hexadecimal Technique Use binary as an intermediary

42. Example 1076 8 = ? 16 1076 8 = 23E 16 1 0 7 6 001 000 111 110 2 3 E

43. Hexadecimal to Octal Hexadecimal Decimal Octal Binary

44. Hexadecimal to Octal Technique Use binary as an intermediary

45. Example 1F0C 16 = ? 8 1F0C 16 = 17414 8 1 F 0 C 0001 1111 0000 1100 1 7 4 1 4

46. Exercise – Convert ... Skip answer Answer Don’t use a calculator! 1AF 703 1110101 33 Hexa- decimal Octal Binary Decimal

47. Exercise – Convert … Answer 1AF 657 110101111 431 1C3 703 111000011 451 75 165 1110101 117 21 41 100001 33 Hexa- decimal Octal Binary Decimal

48. Common Powers (1 of 2) Base 10 T tera 10 12 G giga 10 9 M mega 10 6 k kilo 10 3 m milli 10 -3  micro 10 -6 n nano 10 -9 p pico 10 -12 Symbol Preface Power 1000000000000 1000000000 1000000 1000 .001 .000001 .000000001 .000000000001 Value

49. Common Powers (2 of 2) Base 2 What is the value of “k”, “M”, and “G”? In computing, particularly w.r.t. memory , the base-2 interpretation generally applies G Giga 2 30 M mega 2 20 k kilo 2 10 Symbol Preface Power 1073741824 1048576 1024 Value

50. Example In the lab… 1. Double click on My Computer 2. Right click on C: 3. Click on Properties / 2 30 =

51. Exercise – Free Space Determine the “free space” on all drives on a machine in the lab etc. E: D: C: A: GB Bytes Drive Free space

52. Review – multiplying powers For common bases, add powers 2 6  2 10 = 2 16 = 65,536 or… 2 6  2 10 = 64  2 10 = 64k a b  a c = a b+c

53. Binary Addition (1 of 2) Two 1-bit values pp. 36-38 “two” 10 1 1 1 0 1 1 1 0 0 0 0 A + B B A

54. Binary Addition (2 of 2) Two n -bit values Add individual bits Propagate carries E.g., 10101 21 + 11001 + 25 101110 46 1 1

55. Multiplication (1 of 3) Decimal (just for fun) pp. 39 35 x 105 175 000 35 3675

56. Multiplication (2 of 3) Binary, two 1-bit values 1 1 1 0 0 1 0 1 0 0 0 0 A  B B A

57. Multiplication (3 of 3) Binary, two n -bit values As with decimal values E.g., 1110 x 1011 1110 1110 0000 1110 10011010

58. Fractions Decimal to decimal (just for fun) pp. 46-50 3.14 => 4 x 10 -2 = 0.04 1 x 10 -1 = 0.1 3 x 10 0 = 3 3.14

59. Fractions Binary to decimal pp. 46-50 10.1011 => 1 x 2 -4 = 0.0625 1 x 2 -3 = 0.125 0 x 2 -2 = 0.0 1 x 2 -1 = 0.5 0 x 2 0 = 0.0 1 x 2 1 = 2.0 2.6875

60. Fractions Decimal to binary p. 50 3.14579 .14579 x 2 0.29158 x 2 0.58316 x 2 1.16632 x 2 0.33264 x 2 0.66528 x 2 1.33056 etc. 11.001001...

61. Exercise – Convert ... Skip answer Answer Don’t use a calculator! C.82 3.07 101.1101 29.8 Hexa- decimal Octal Binary Decimal

62. Exercise – Convert … Answer C.82 14.404 1100.10000010 12.5078125 3.1C 3.07 11.000111 3.109375 5.D 5.64 101.1101 5.8125 1D.CC… 35.63… 11101.110011… 29.8 Hexa- decimal Octal Binary Decimal

63. Thank you Next topic