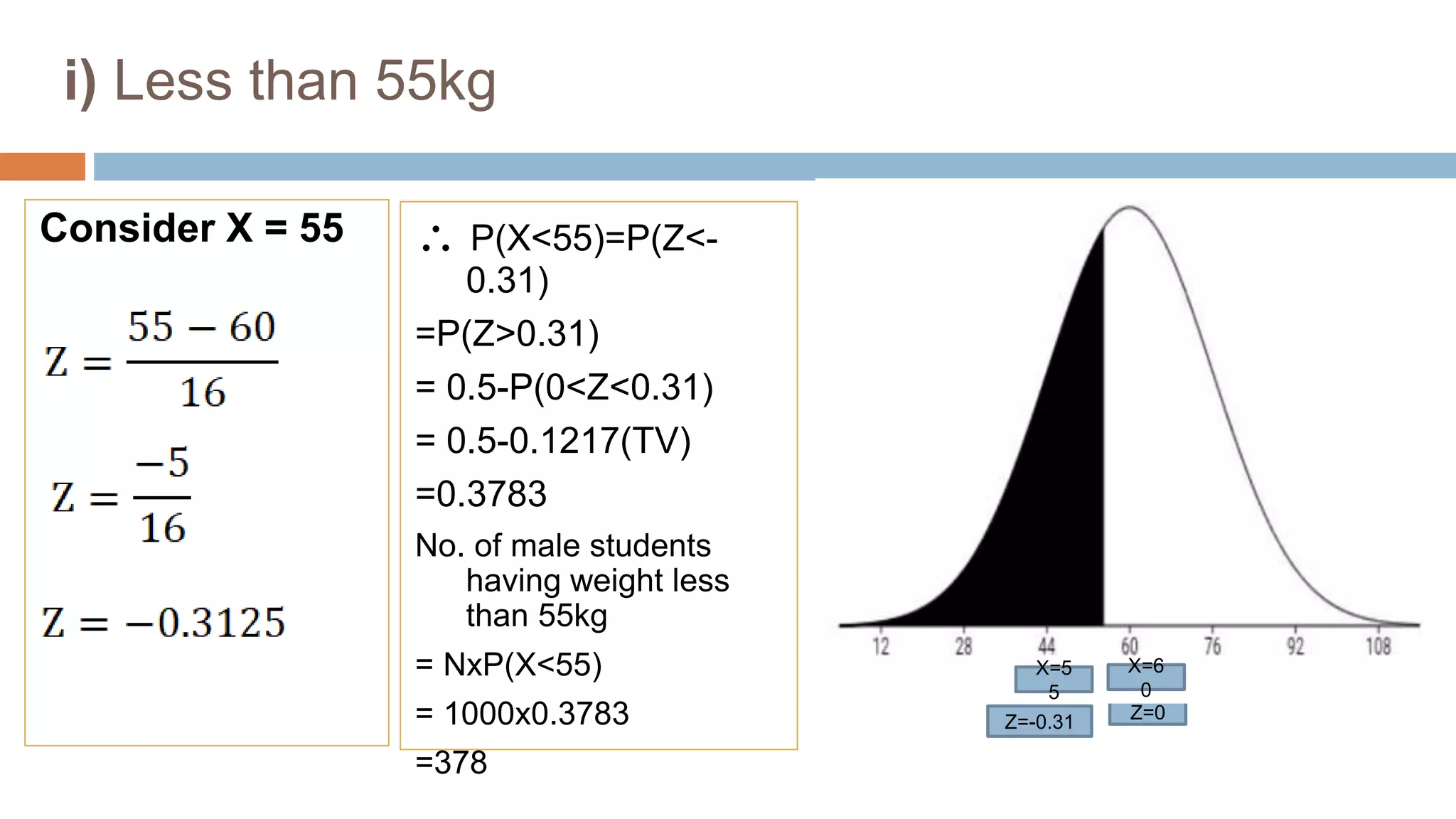
The document summarizes finding values for a normal distribution based on given information about 1000 male students. 1) The mean weight is 60kg with a standard deviation of 16kg. 2) The number of students weighing less than 55kg is 378. The number weighing more than 70kg is 264. The number between 45kg and 65kg is 448. 3) To find the lowest weight of the 100 heaviest students, it is calculated that the z-score is 1.28, making the lowest weight 80.48kg.

1. Normal
Distribution –Find the
value of X
SUNDARA B. N.
Assistant
Professor

2. Problem
In a university the mean weight of 1000 male
students is 60kg and Standard Deviation is
16kg
a) Find the number of male students having their
weights
i. Less than 55kg
ii. More than 70 kg
iii. Between 45 kg and 65 kg
b) What is the lowest weight of the 100 heaviest
male students?

3. Given Information
Here we are given that
N=1000
μ = 60
σ = 16
 X~N(60,256),
We know that is X~N(μ, σ²), then the S.N.V is given
by
Z = X – μ
σ

4. i) Less than 55kg
Consider X = 55  P(X<55)=P(Z<-
0.31)
=P(Z>0.31)
= 0.5-P(0<Z<0.31)
= 0.5-0.1217(TV)
=0.3783
No. of male students
having weight less
than 55kg
= NxP(X<55)
= 1000x0.3783
=378
Z=-0.31 Z=0
X=6
0
X=5
5

5. ii) More than 70 kg
Consider X =
70
 P(X>70)=P(Z>0.63)
= 0.5-
P(0<Z<0.63)
= 0.5-0.2357(TV)
=0.2643
No. of male students
having weight more
than 70kg
= NxP(X>70)
= 1000x0.2643
=264
Z=0 Z=0.63
X=6
0
X=7
2

6. iii) Between 45 kg and 65 kg
Consider X = 45 and X =
65
 P(45<X<65)=P(-.94<X<0.31)
= P(-0.94<X<0)+P(0<Z<0.31)
= P(0<Z<0.94)+P(0<Z<0.31)
= 0.3264+0.1217 (TV)
=0.4481
No. of male students having
weight between 45kg & 65kg
= P(45<X<65)
= 1000x0.4481
=448
X=8
0
Z=0
X=6
5
Z=0.3
1
X=4
5
Z=-0.94

7. b) What is the lowest weight of the 100
heaviest male students?
Let x₁ be the lowest weight
amongst 100 heaviest
students.
Now, for X=x₁,
P(Z≥z₁)=
P(0≤Z≤z₁) = 0.1
P(0≤Z≤z₁) = 0.5-0.1=0.4
z₁= 1.28 (From Table)
x₁=60+16x1.28=60+20.48=80.
48
 the lowest weight of
100 heaviest male
students is 80.48kg
X=μ X=x₁