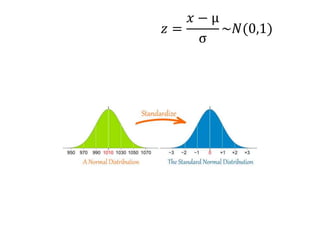
The document discusses the standard normal distribution and provides examples of calculating probabilities and number of occurrences given a normal distribution. It begins by defining the standard normal variate Z as representing the number of standard deviations a point is from the mean. It then provides 10 problems as examples, such as calculating the number of students over a certain height given the mean and standard deviation of student heights, or the probability of a value falling within an interval of a normal distribution.

1. Standardized Normal
Distribution

2. Probability Density Function

3. 𝑧 =
𝑥 − µ
σ
~𝑁(0,1)

4. Standard Normal Variate Z
Z represents the number of standard deviations,
a point X is away from the mean of the
distribution
Using the properties of Mean and SD
a. The algebraic sum of deviations of all values
from their mean is 0
b. SD is independent of change of origin
c. Hence Mean of Z values =0 and SD of Z values =1
Standard variate Z has mean 0 and SD 1

5. Z
• Identify and describe the exact location of
every point in a distribution
• Compare 2 or more distributions
• Sign of Z indicates if given point is above or
below mean
• Value of Z tells the distance between the
point (x) and the Mean in terms of Standard
Deviations ( The Professor Example of test
scores)

6. Problems
• Q1 ) Assuming the mean height of students in
an normal distribution to be 68.22 inches with
a variance of 10.8 inches. How many students
in an Institute of 1000 students would you
expect to be over 6ft tall

7. X=72,Sd =3.28 ,Z=(72-68.22)/3.28=1.15
Ztable=0.3749
Area under curve =0.5-0.3749=0.1251
Answer =0.1251*1000=125 students

8. • Q2) The mean height of 18 year old boys is 70
inches. If its normally distributed and SD is 2.5
inches , find the probability of getting a
student taller than 74 inches

9. Solution
• X = 74
• Mean = 70
• Sd=2.5
• Z= (74-70)/2.5 =1.6
• From Tables Z=1.6 is 0.4452
• Area to the right of Z =1.6 is 0.5-
0.4452=0.0548
• Probability =0.0548 or 5.4%

10. • Q3) Income of group of 5000 persons were
found to be normally distributed with mean
=Rs 900 and SD=Rs 75. What was the highest
income among the poorest 200?

11. Solution : Rs 768.75

12. • Q4 )Let x be a continuous variable and follows
a normal distribution with mean 12 and Sd 2
What is probability that the value of x selected
at random lies in the interval (11,14)?

13. Answer =0.5328

14. • Q5) An Airline has a policy of employing
women whose height is between 62 and 69
inches .If the height of women is normally
distributed with mean of 64 inches and SD of
3 inches, out of 1000 applicants find number
of applicants
a) Too tall
b) Too short
c)Acceptable height

15. Solution

16. • Q6) The average weekly food expenditure of
families in a certain area has a normal
distribution with mean of Rs 125 and SD of Rs
25
• What is the probablity that a family selected
at random from this area will have an average
weekly expenditure on food item in excess of
Rs 175

17. Solution 6

18. • Q7 ) The finance department of a Pharma
Company is concerned that the ageing machinery
on its production line is causing losses by putting
too much on average of certain product into
each container .A check on the line shows that
the mean amount being put into a container is
499.5 ml with sd of 0.8ml
• If normally distributed , what % of containers will
contain more than the notional content of 500 ml

19. Solution 7

20. • Q8 )Assuming that mean height of soldiers to
be 68.22 unit of height with variance of 10.8
sq units .How many soldiers in the regisment
of 10,000 would you expect to be over 72
units tall

21. Solution 8
• Z= 72-68.22/3.28= 1.15
• Area between Z=0 to Z=1.15 = 0.3749
• Area to right of Z=1.15 is 0.5-0.3749=0.1251
• Number of soldiers over 72 units tall =
10000*0.1251 =1251

22. • Q9 ) Packets of certain washing powder are
filled with an automatic machine with average
weight of 5Kg and SD of 50 gms.If the weights
of packets are normally distributed , find the
% of packets having a weight abover 5.1Kg

23. Solution 9
• Z= 5.1-5/0.05=2
• Area covered by packets weighing above 5.1
= 0.5-0.4772 =0.0228 or 28%

24. • Q10 )If height of 300 students is normally
distributed with mean 64.5 inch and SD 3.3
inch
a) How many students have height less than 5 ft
b) Between 5ft & 5ft 9inch

25. Solution 10
• P( X<60) =P (Z< 60-64.5/3.3)
• Z=-1.36
• Z table between Z=0 and Z =1.36 =.4131
Due to symmetry Z=1.36=-1.36
Area under curve 0.5-0.4131 = 0.0869
No of students = 300*0.0869=26
Ans b) 248 students ( Z=+-1.36) =0.4131*2