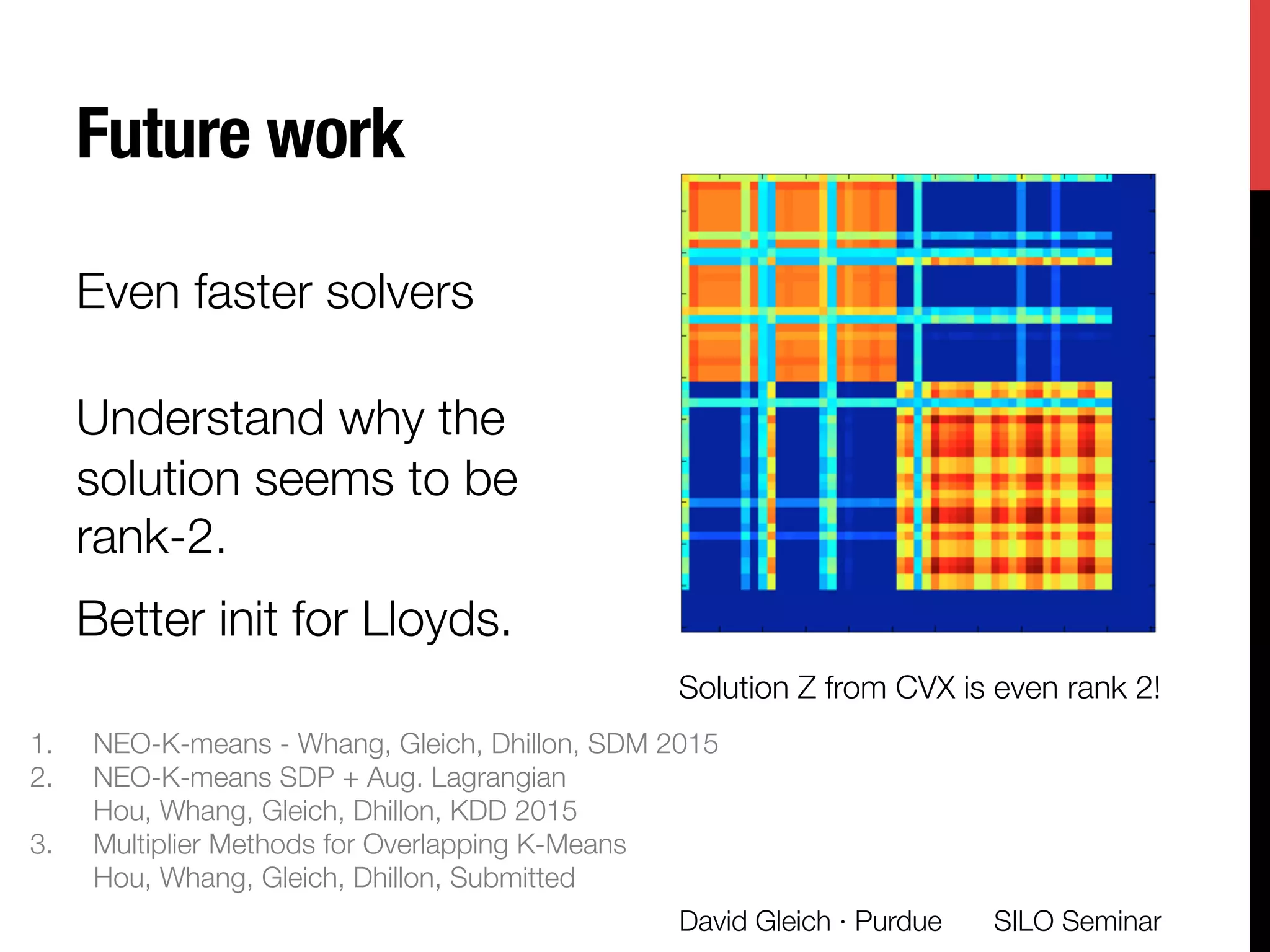
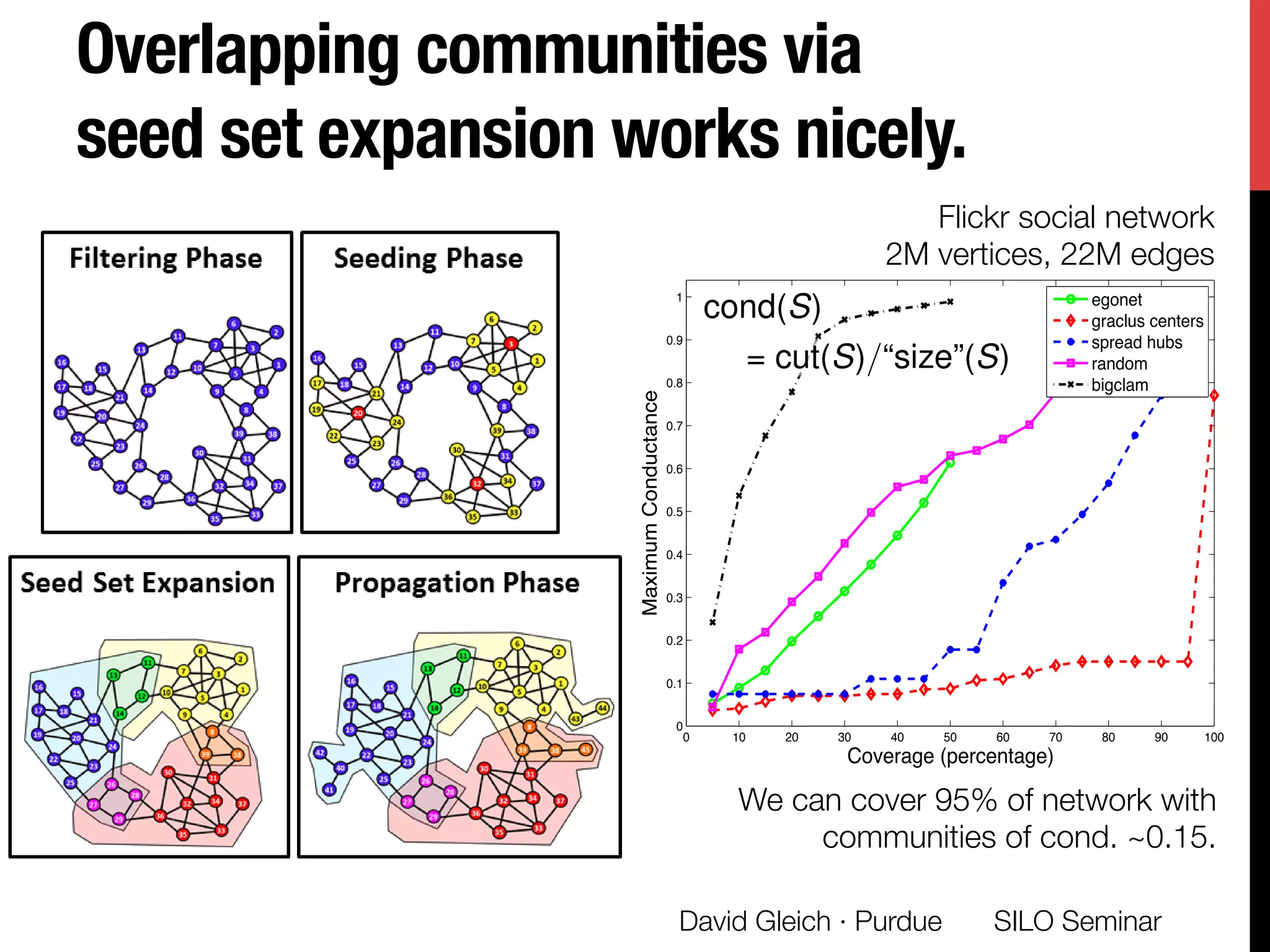
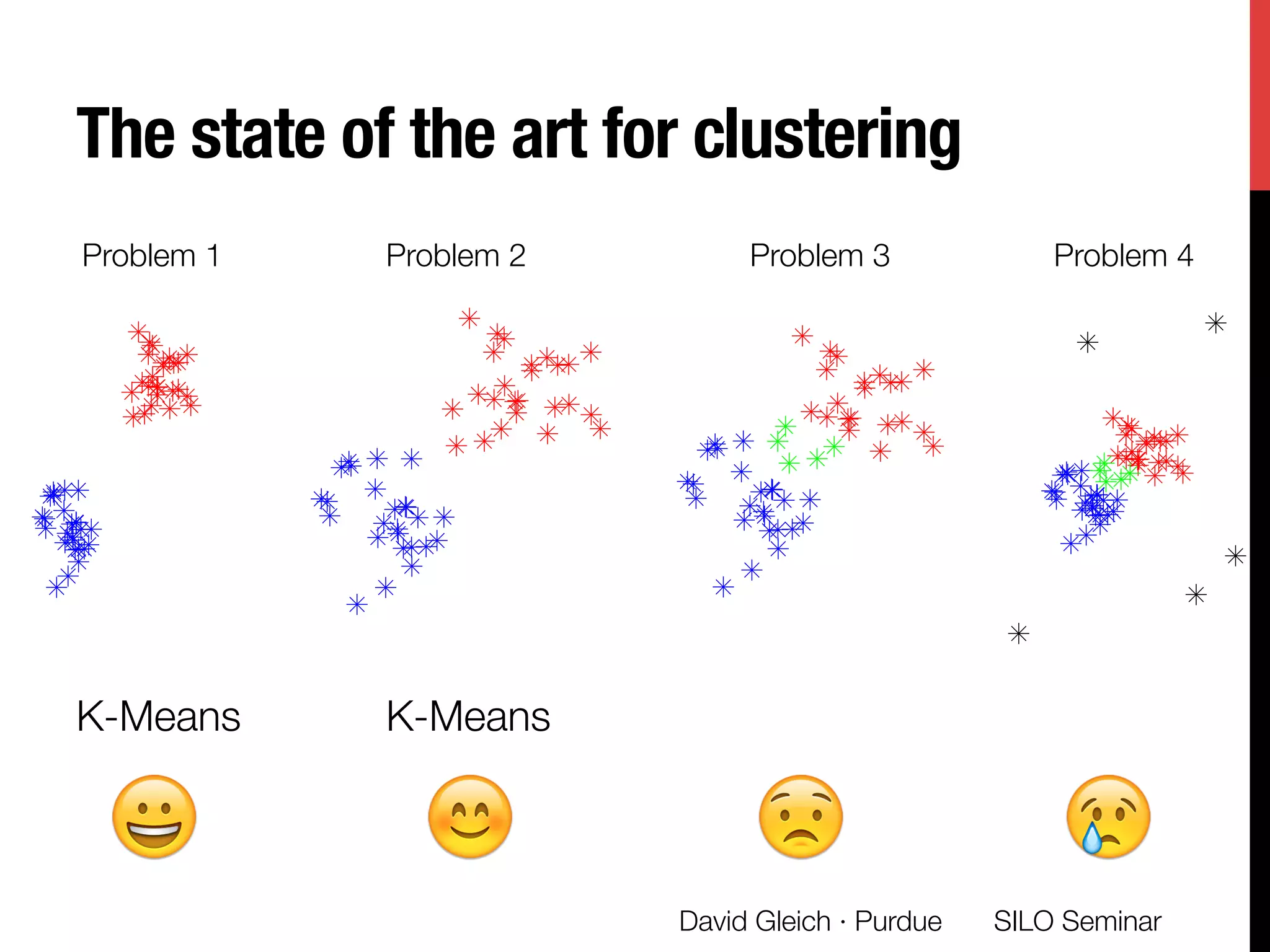
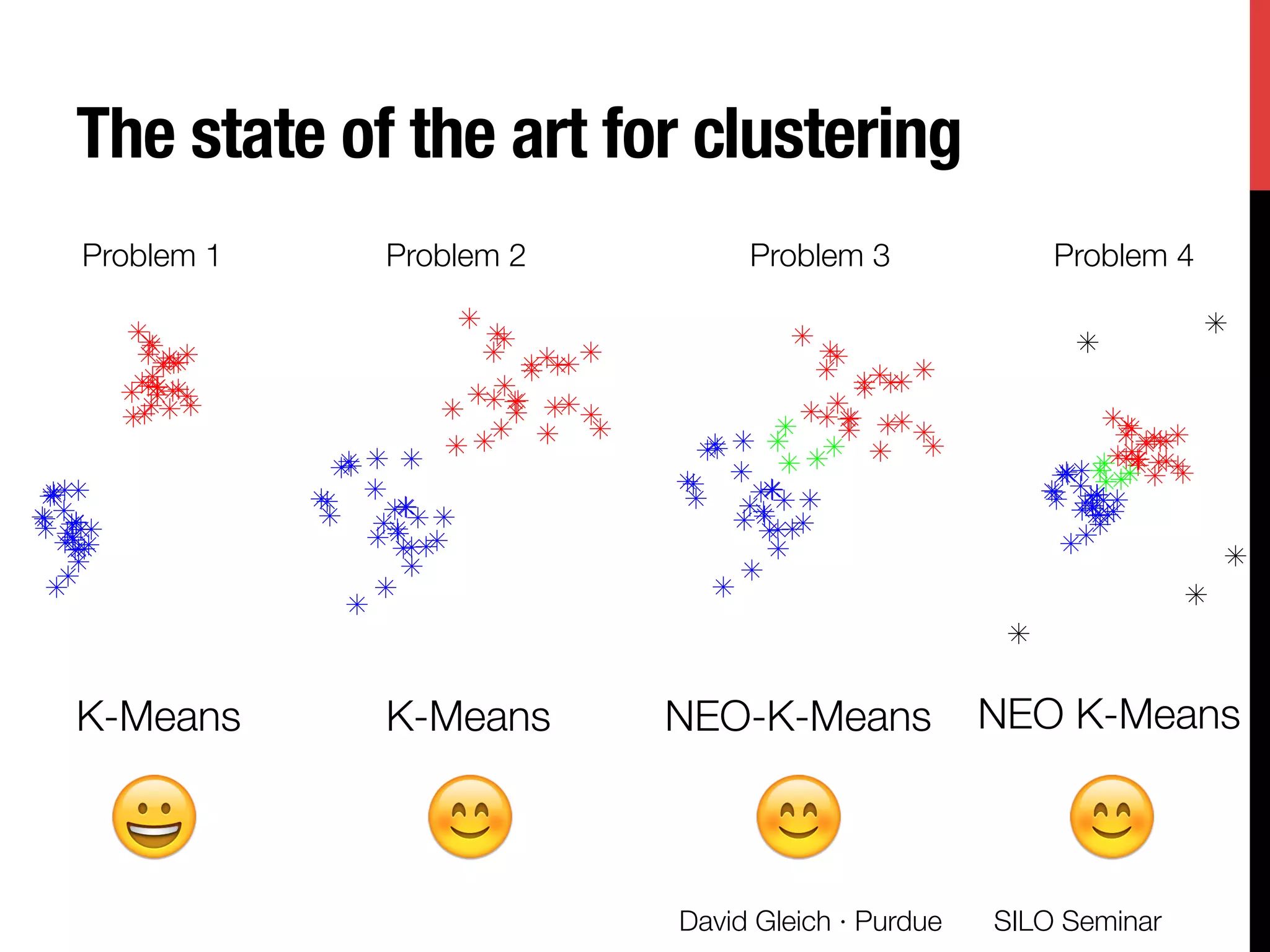
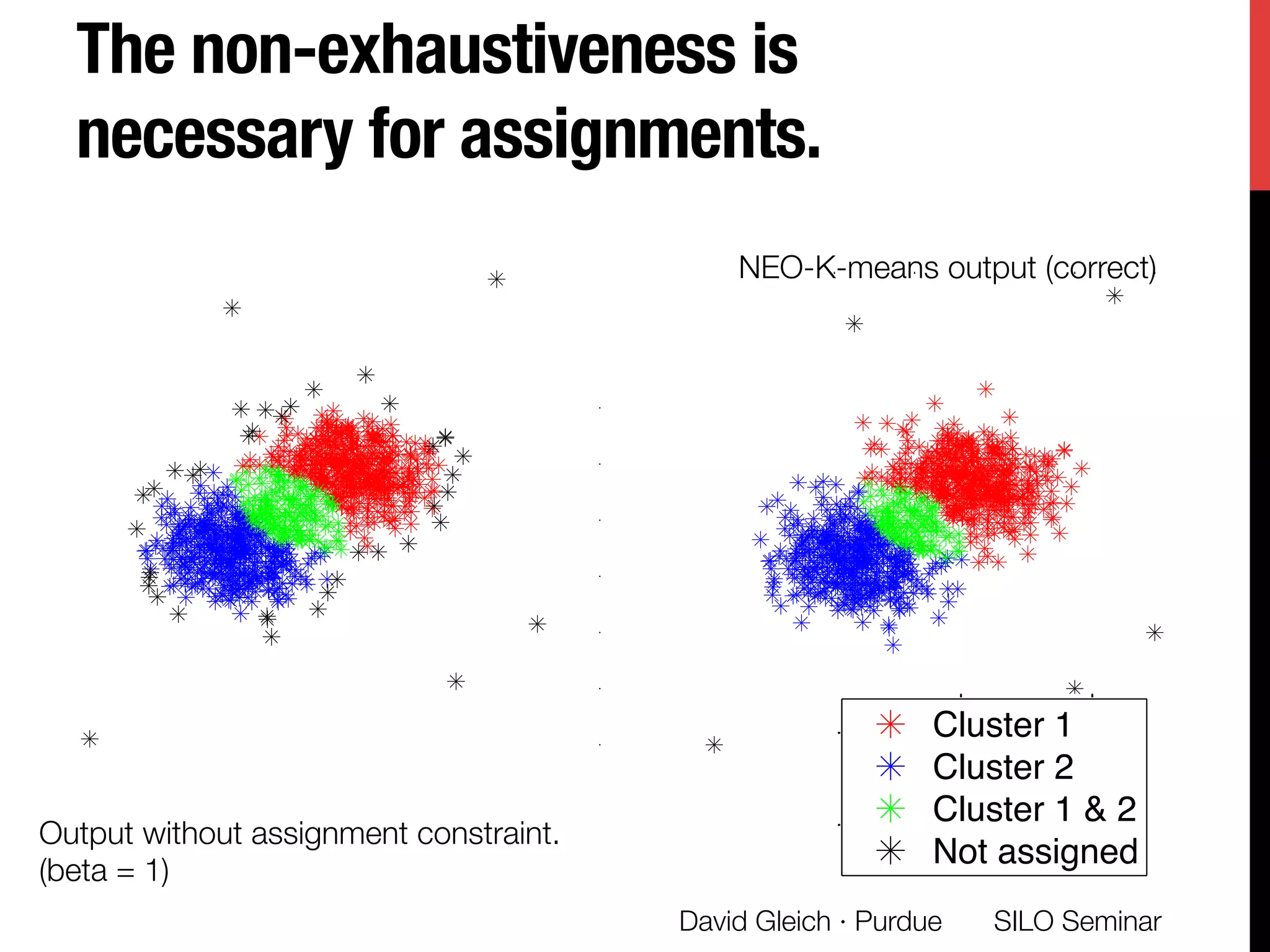
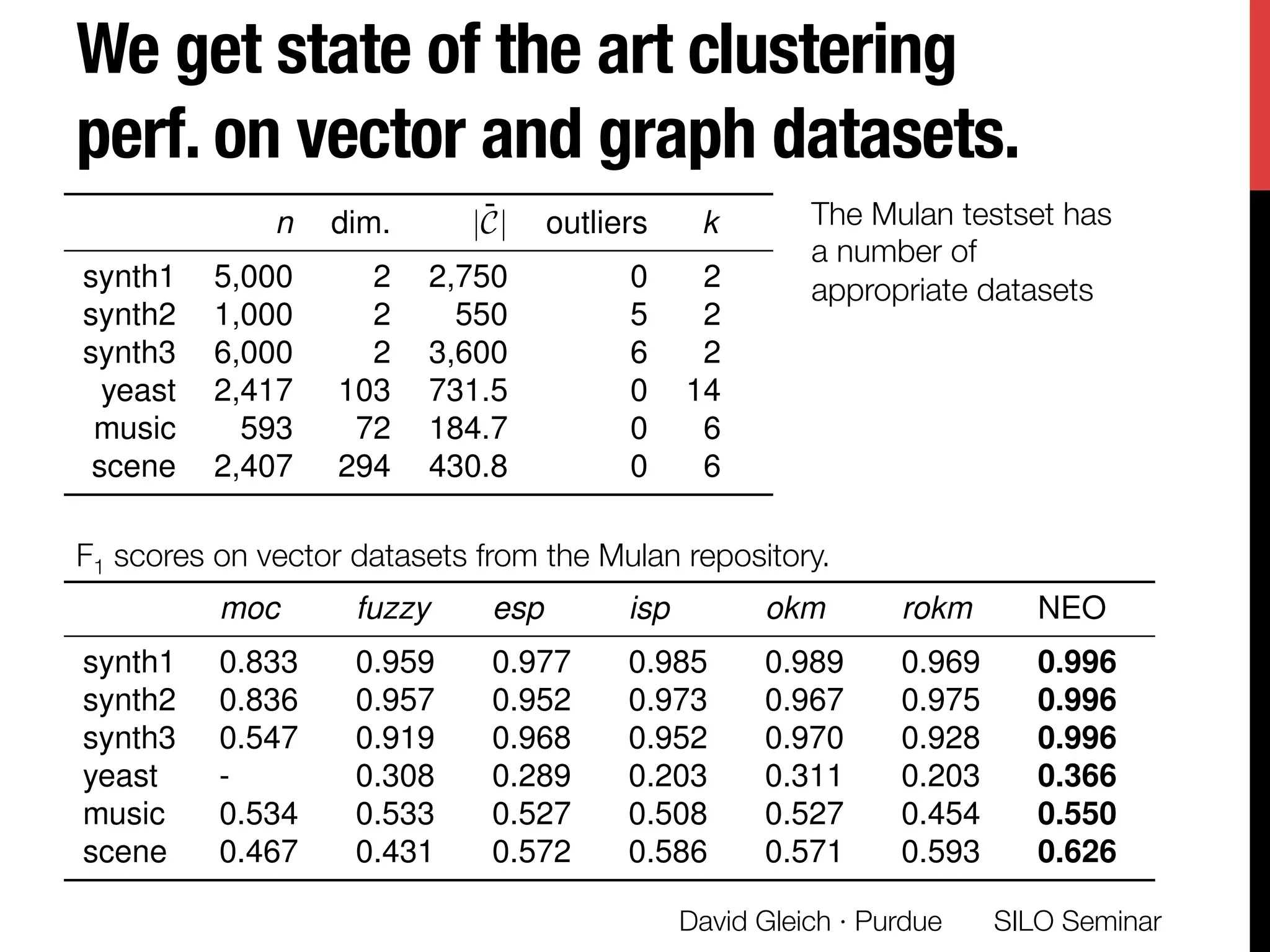
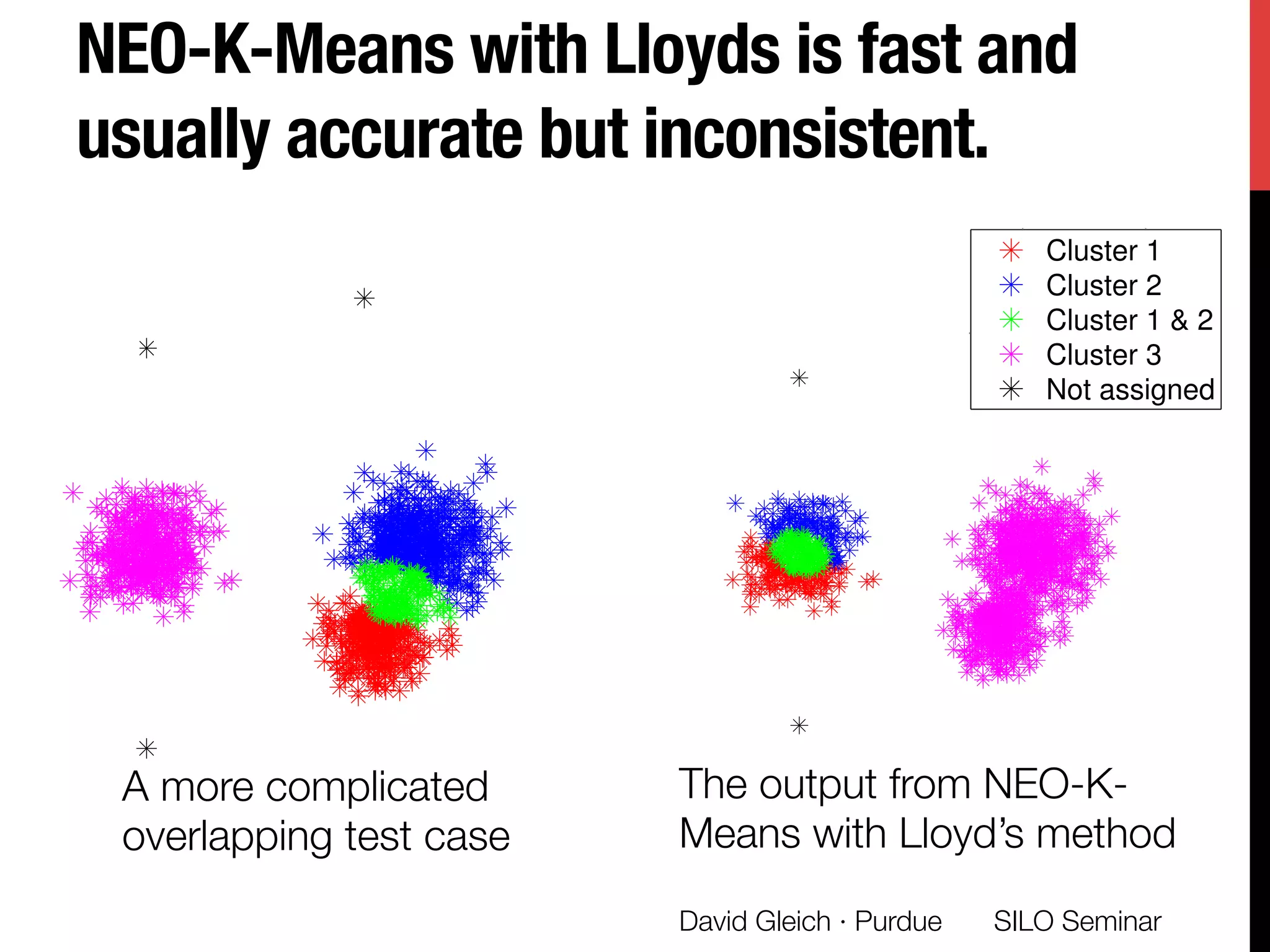
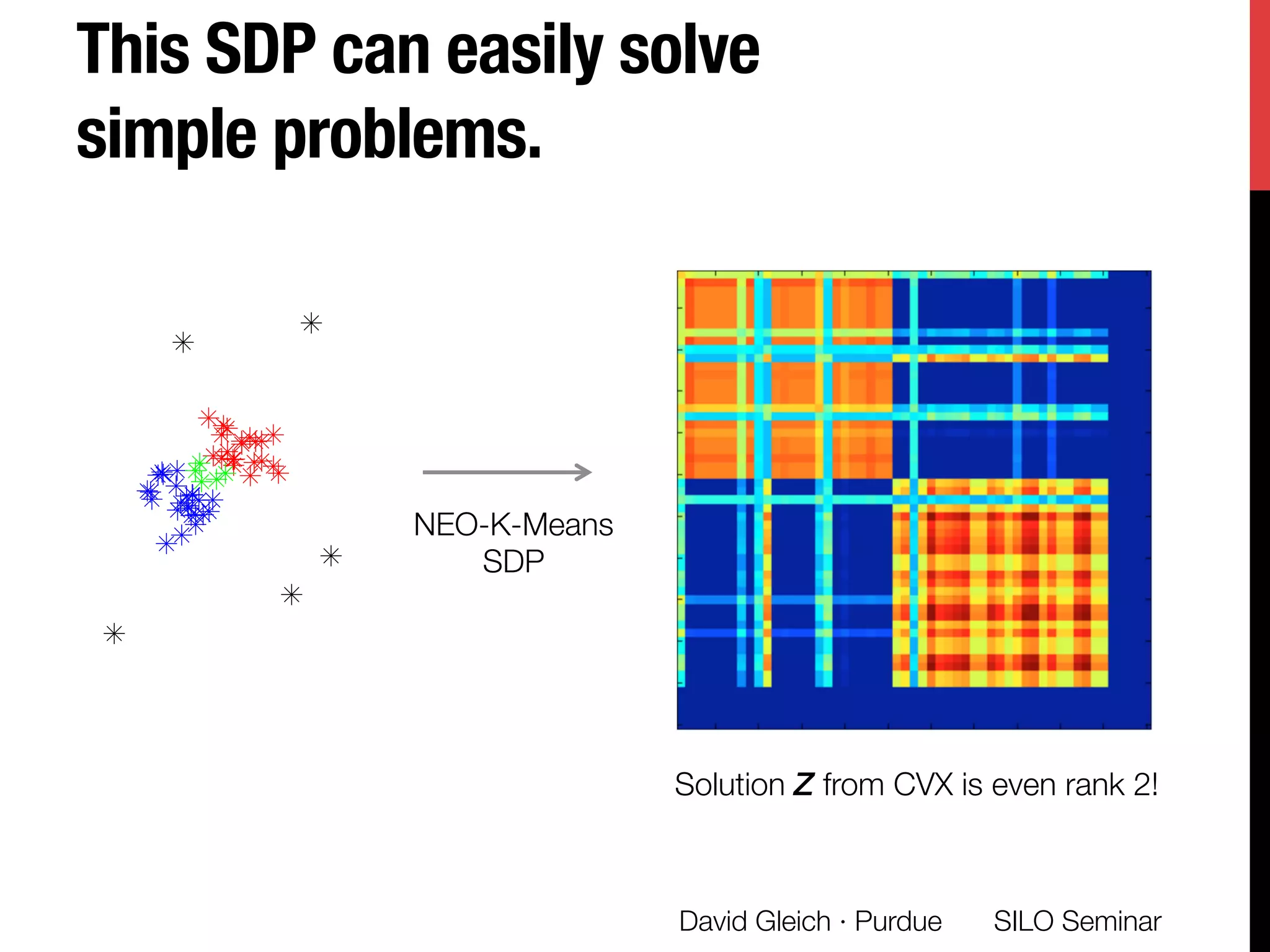
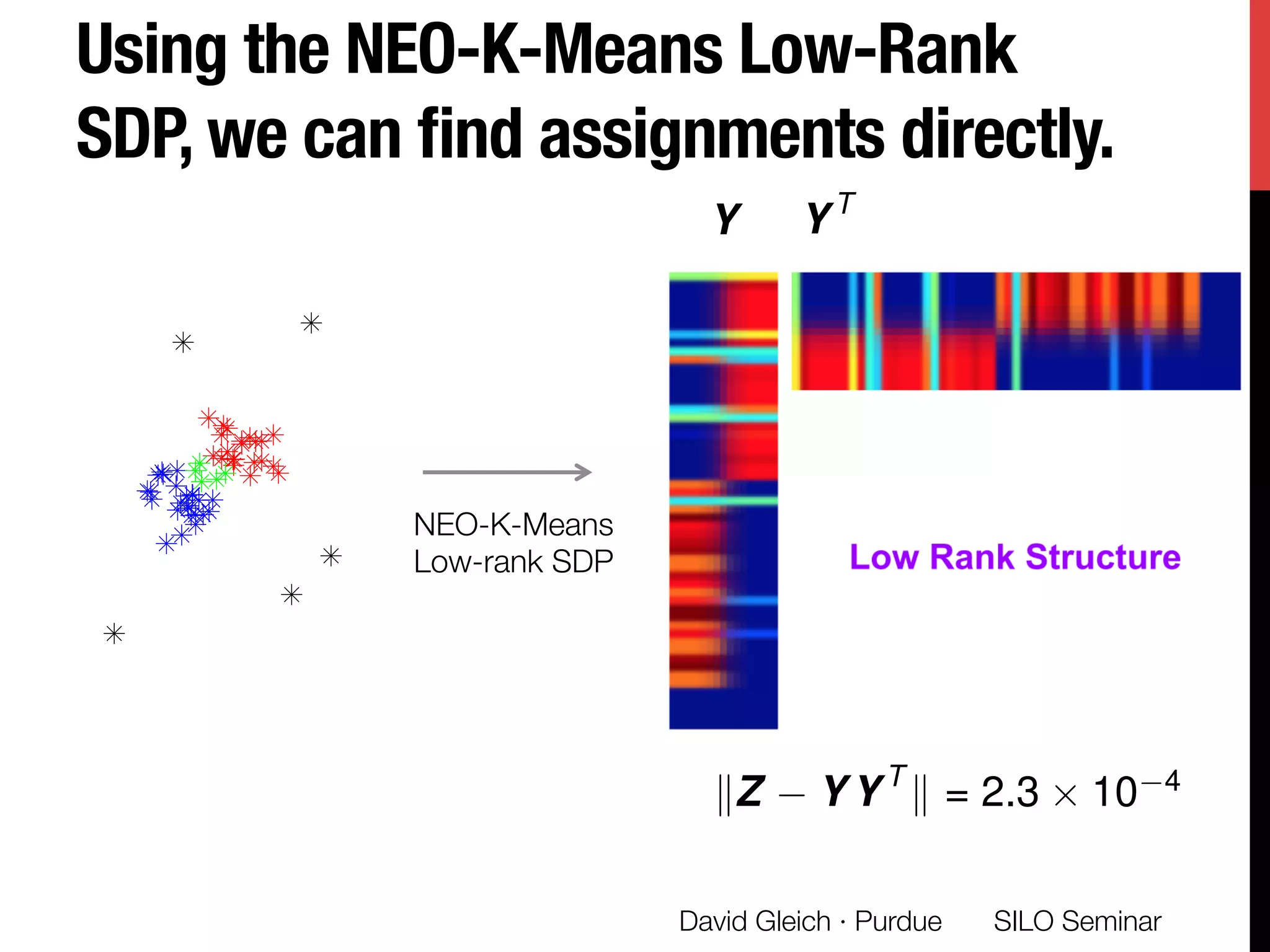
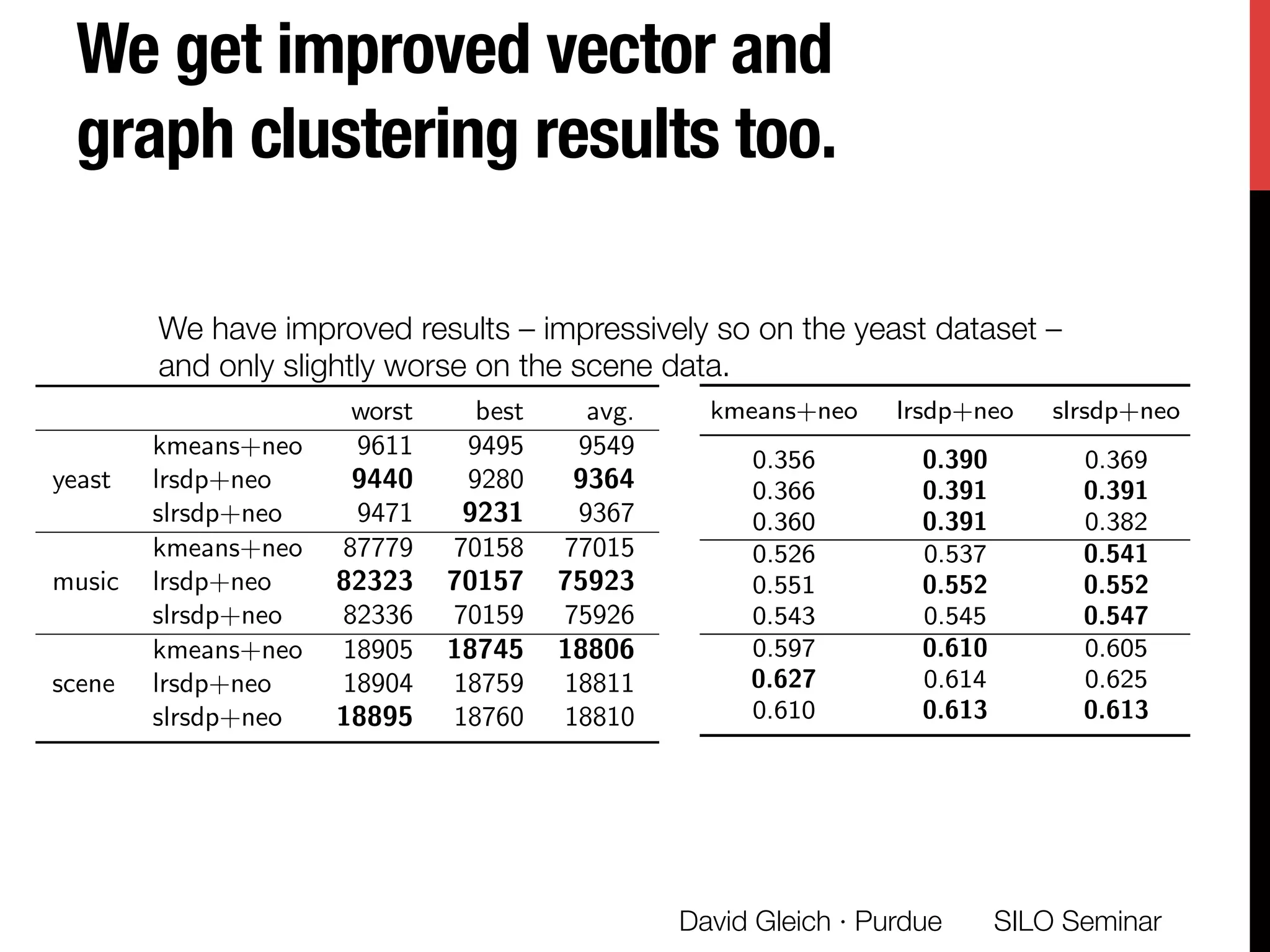
The document presents a study on non-exhaustive overlapping k-means clustering, addressing the challenges of clustering real-world data with overlapping clusters, particularly in social networks and biological contexts. It introduces a neo-k-means framework that balances overlaps and outliers, providing an optimization method for clustering that improves community detection performance. The research discusses key theoretical contributions and practical implications, including techniques for graph-based and vector datasets.






![The NEO-K-means objective
balances overlap and outliers.
SILO Seminar
David Gleich · Purdue
minimize
P
ij Uij kxi mj k
2
subject to Uij is binary
trace(UT
U) = (1 + ↵)n (↵n overlap)
eT
Ind[Ue] (1 )n (up to n outliers)
mj = 1P
i Ui j Uij xi
· If ↵, = 0, then we get back to K-means.
· Automatically choose ↵, based on K-means.
😊
1. Make (1 + ↵)n total assignments.
2. Allow up to n outliers.](https://image.slidesharecdn.com/neokm-gleich-seminar-151123022702-lva1-app6892/75/Non-exhaustive-Overlapping-K-means-11-2048.jpg)

![The Weighted, Kernel "
NEO-K-Means objective.
• Introduce weights for each data point.
• Introduce feature maps for each data point too.
SILO Seminar
David Gleich · Purdue
minimize
P
ij Uij wi k (xi ) mj k
2
subject to Uij is binary
trace(UT
U) = (1 + ↵)n (↵n overlap)
eT
Ind[Ue] (1 )n (up to n outliers)
mj = 1P
i Uij wi
wi Uij xi
X
ij
Uij wi k (xi ) mj k
2
=
X
ij
Uij wi Kii
uj WKWuj
uT
j Wuj
!
Theorem If K = D 1
+ D 1
AD 1
, then the NEO-K-Means objective
is equivalent to overlapping conductance.
NOTE](https://image.slidesharecdn.com/neokm-gleich-seminar-151123022702-lva1-app6892/75/Non-exhaustive-Overlapping-K-means-14-2048.jpg)

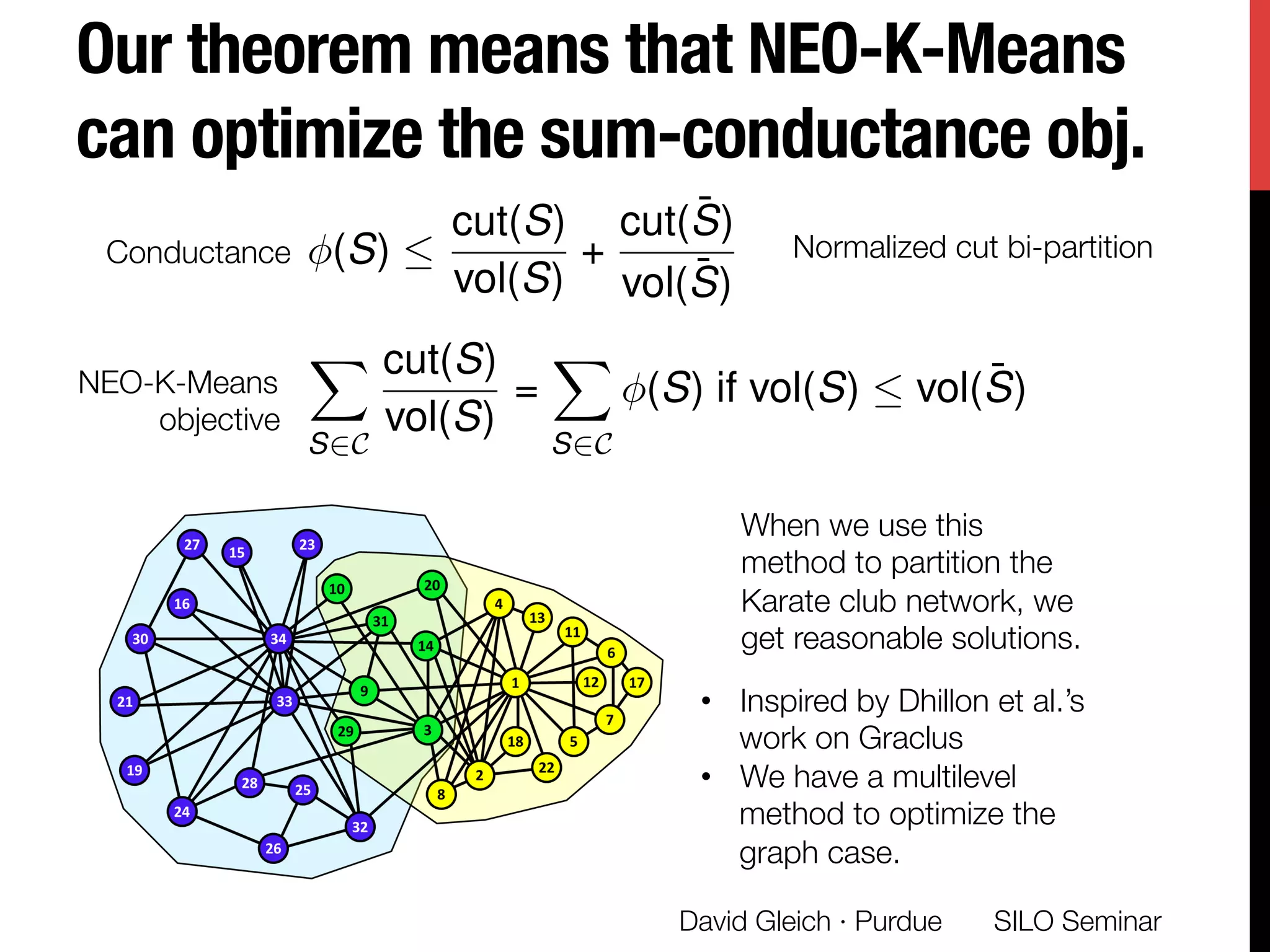
![Conductance communities
Conductance is one of the most
important community scores [Schaeffer07]
The conductance of a set of vertices is
the ratio of edges leaving to total edges:
Equivalently, it’s the probability that a
random edge leaves the set.
Small conductance ó Good community
(S) =
cut(S)
min vol(S), vol( ¯S)
(edges leaving the set)
(total edges
in the set)
David Gleich · Purdue
cut(S) = 7
vol(S) = 33
vol( ¯S) = 11
(S) = 7/11
SILO Seminar](https://image.slidesharecdn.com/neokm-gleich-seminar-151123022702-lva1-app6892/75/Non-exhaustive-Overlapping-K-means-16-2048.jpg)








![We use an augmented Lagrangian
method to optimize this problem
SILO Seminar
David Gleich · Purdue
Journal on Optimization, 18(1):186–205, 2007.
[29] K. Trohidis, G. Tsoumakas, G. Kalliris, and I. P.
Vlahavas. Multi-label classification of music into
emotions. In International Conference on Music
Information Retrieval, pages 325–330, 2008.
[30] J. J. Whang, I. S. Dhillon, and D. F. Gleich.
Non-exhaustive, overlapping k-means. In Proceedings
of the SIAM International Conference on Data
Mining, pages 936–944, 2015.
[31] J. J. Whang, D. Gleich, and I. S. Dhillon. Overlapping
community detection using seed set expansion. In
ACM International Conference on Information and
Knowledge Management, pages 2099–2108, 2013.
[32] L. F. Wu, T. R. Hughes, A. P. Davierwala, M. D.
Robinson, R. Stoughton, and S. J. Altschuler.
Large-scale prediction of saccharomyces cerevisiae
gene function using overlapping transcriptional
clusters. Nature Genetics, 31(3):255–265, June 2002.
[33] E. P. Xing and M. I. Jordan. On semidefinite
relaxations for normalized k-cut and connections to
spectral clustering. Technical Report
UCB/USD-3-1265, University of California, Berkeley,
2003.
[34] J. Yang and J. Leskovec. Overlapping community
detection at scale: a nonnegative matrix factorization
approach. In ACM International Conference on Web
Search and Data Mining, pages 587–596, 2013.
[35] S. X. Yu and J. Shi. Multiclass spectral clustering. In
IEEE International Conference on Computer Vision -
Volume 2, 2003.
APPENDIX
A. AUGMENTED LAGRANGIANS
The augmented Lagrangian framework is a general strat-
egy to solve nonlinear optimization problems with equality
tion and the gradient vector.
B. GRADIENTS FOR NEO-LR
We now describe the analytic form of the gradients for the
augmented Lagrangian of the NEO-LR objective and a brief
validation that these are correct. Consider the augmented
Lagrangian (5). The gradient has five components for the
five sets of variables: Y , f, g, s and r:
rY LA(Y , f, g, s, r; , µ, , ) =
2KY eµT
Y µeT
Y
2( 1 (tr(Y T
W 1
Y ) k))W 1
Y
+ (Y Y T
eeT
Y + eeT
Y Y T
Y ) (W feT
Y + efT
W Y )
rf LA(Y , f, g, s, r; , µ, , ) =
d + W µ (W Y Y T
e W 2
f) 2e + (eT
f (1 + ↵)n)e
+ (f g s)
rgLA(Y , f, g, s, r; , µ, , ) =
(f g s) 3e + (eT
g (1 )n r)e
rsLA(Y , f, g, s, r; , µ, , ) = (f g s)
rrLA(Y , f, g, s, r; , µ, , ) = 3 (eT
g (1 )n r)
Using analytic gradients in a black-box solver such as L-
BFGS-B is problematic if the gradients are even slightly in-
correctly computed. To guarantee the analytic gradients we
derive are correct, we use forward finite di↵erence method
to get numerical approximation of the gradients based on
the objective function. We compare these with our analytic
gradient and expect to see small relative di↵erences on the
order of 10 5
or 10 6
. This is exactly what Figure 4 shows.
ous studies of low-rank sdp approximations [6].
Let = [ 1; 2; 3] be the Lagrange multipliers associated
th the three scalar constraints (s), (u), (w), and µ and
be the Lagrange multipliers associated with the vector
nstraints (t) and (v), respectively. Let 0 be a penalty
rameter. The augmented Lagrangian for (4) is:
LA(Y, f, g, s, r; , µ, , ) =
fT
d trace(Y T
KY )
| {z }
the objective
1(trace(Y T
W 1
Y ) k)
+
2
(trace(Y T
W 1
Y ) k)2
µT
(Y Y T
e W f)
+
2
(Y Y T
e W f)T
(Y Y T
e W f)
2(eT
f (1 + ↵)n) +
2
(eT
f (1 + ↵)n)2
T
(f g s) +
2
(f g s)T
(f g s)
3(eT
g (1 )n r)
+
2
(eT
g (1 )n r)2
(5)
t each step in the augmented Lagrangian solution frame-
ork, we solve the following subproblem:
minimize LA(Y , f, g, s, r; , µ, , )](https://image.slidesharecdn.com/neokm-gleich-seminar-151123022702-lva1-app6892/75/Non-exhaustive-Overlapping-K-means-30-2048.jpg)










![SILO Seminar
David Gleich · Purdue
plot(x)
0 2 4 6 8 10
x 10
5
0
0.02
0.04
0.06
0.08
0.1
10
0
10
2
10
4
10
6
10
−15
10
−10
10
−5
10
0
10
0
10
2
10
4
10
6
10
−15
10
−10
10
−5
10
0
nonzeros
Crawl of flickr from 2006 ~800k nodes, 6M edges, beta=1/2
(I P)x = (1 )s
nnz(x) ⇡ 800k
kD1
(xx⇤
)k1"
Localized solutions of diffusion equations in large graphs.
Joint with Kyle Kloster. WAW2013, KDD2014, WAW2015; J. Internet Math.
the answer [5]. Thus, just as in scientific
computing, marrying the method to
the model is key for the best scientific
computing on social networks.
Ultimately, none of these steps dif-
fer from the practice of physical sci-
entific computing. The challenges in
creating models, devising algorithms,
validating results, and comparing
models just take on different chal-
lenges when the problems come from
social data instead of physical mod-
els. Thus, let us return to our starting
question: What does the matrix have
to do with the social network? Just as
in scientific computing, many inter-
esting problems, models, and meth-
ods for social networks boil down to
matrix computations. Yet, as in the
expander example above, the types of
matrix questions change dramatical-
ly in order to fit social network mod-
els. Let’s see what’s been done that’s
enticingly and refreshingly different
from the types of matrix computa-
tions encountered in physical scien-
tific computing.
EXPANDER GRAPHS AND
PARALLEL COMPUTING
Recently, a coalition of folks from aca-
demia, national labs, and industry set
out to tackle the problems in parallel
computing and expander graphs. They
established the Graph 500 benchmark
(http://www.graph500.org) to measure
the performance of a parallel com-
puter on a standard graph computa-
tion with an expander graph. Over the
past three years, they’ve seen perfor-
mance grow by more than 1,000-times
Diffusion
in a plate
Movie
interest in
diffusion
The network, or mesh, from a typical problem in scientific computing
n a low dimensional space—think of two or three dimensions. These physical
ut limits on the size of the boundary or “surface area” of the space given its
No such limits exist in social networks and these two sets are usually about
size. A network with this property is called an expander network.
Size of set » Size of boundary
“Networks”
from PDEs
are usually
physical
Social networks
are expanders](https://image.slidesharecdn.com/neokm-gleich-seminar-151123022702-lva1-app6892/75/Non-exhaustive-Overlapping-K-means-44-2048.jpg)