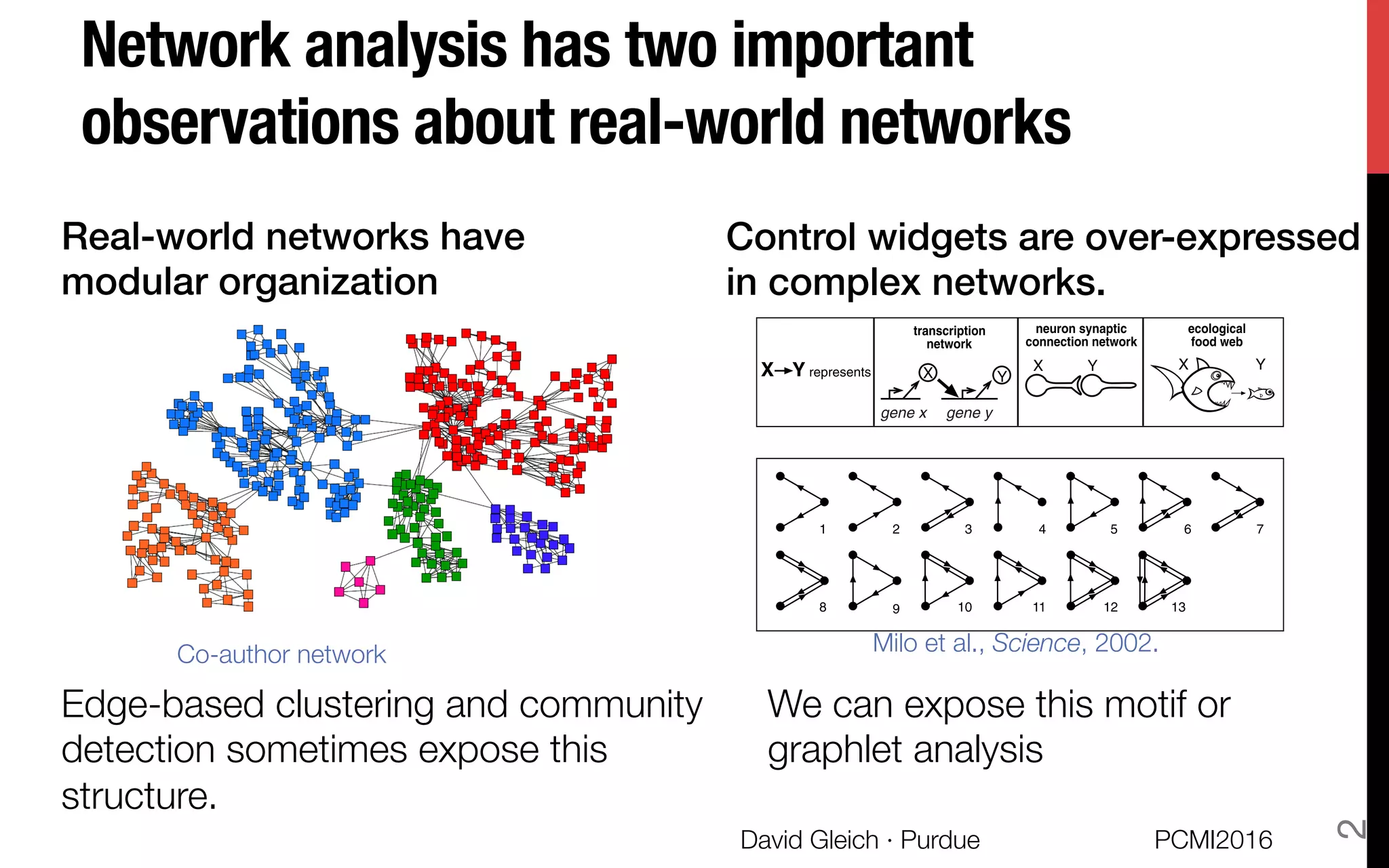
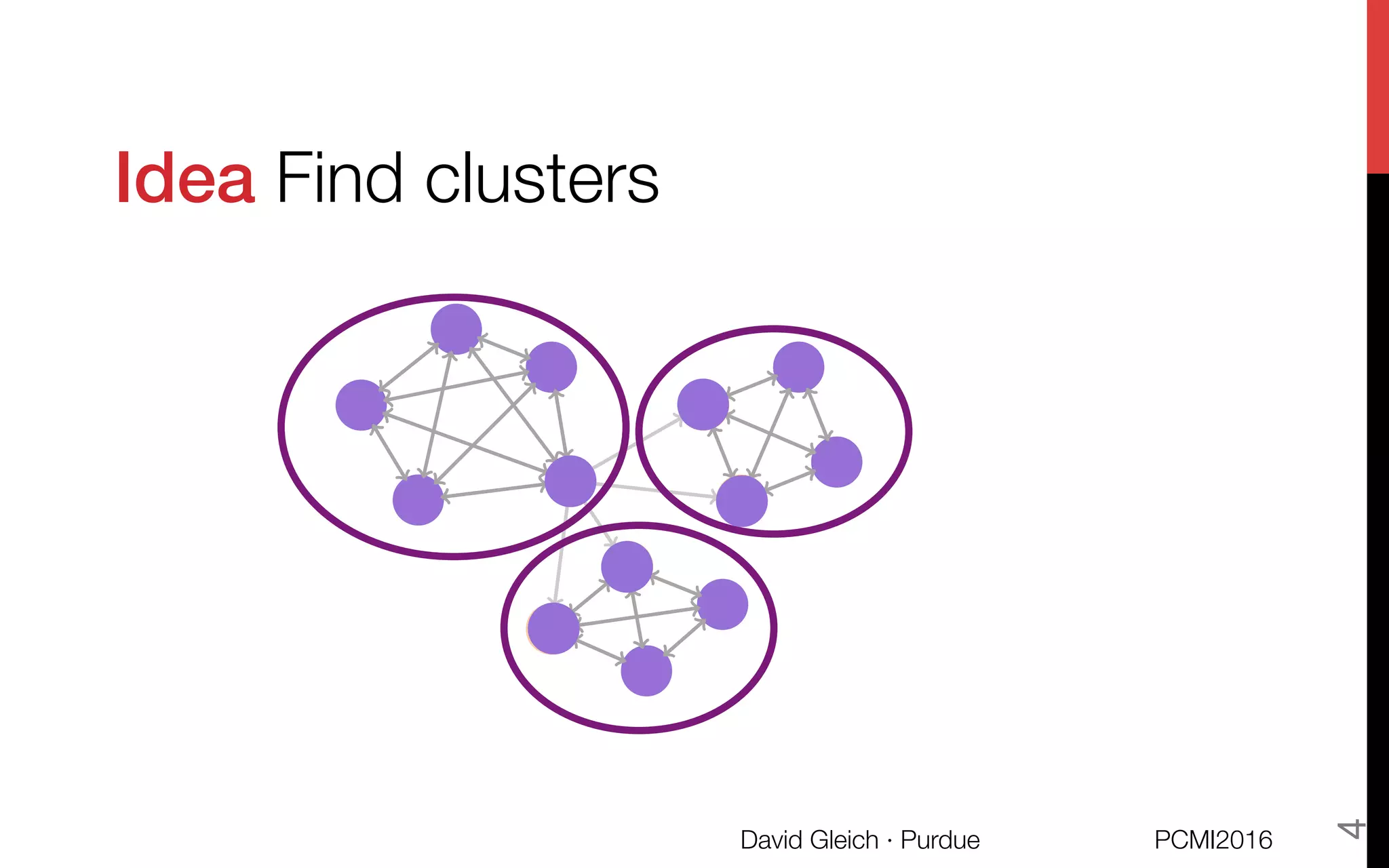
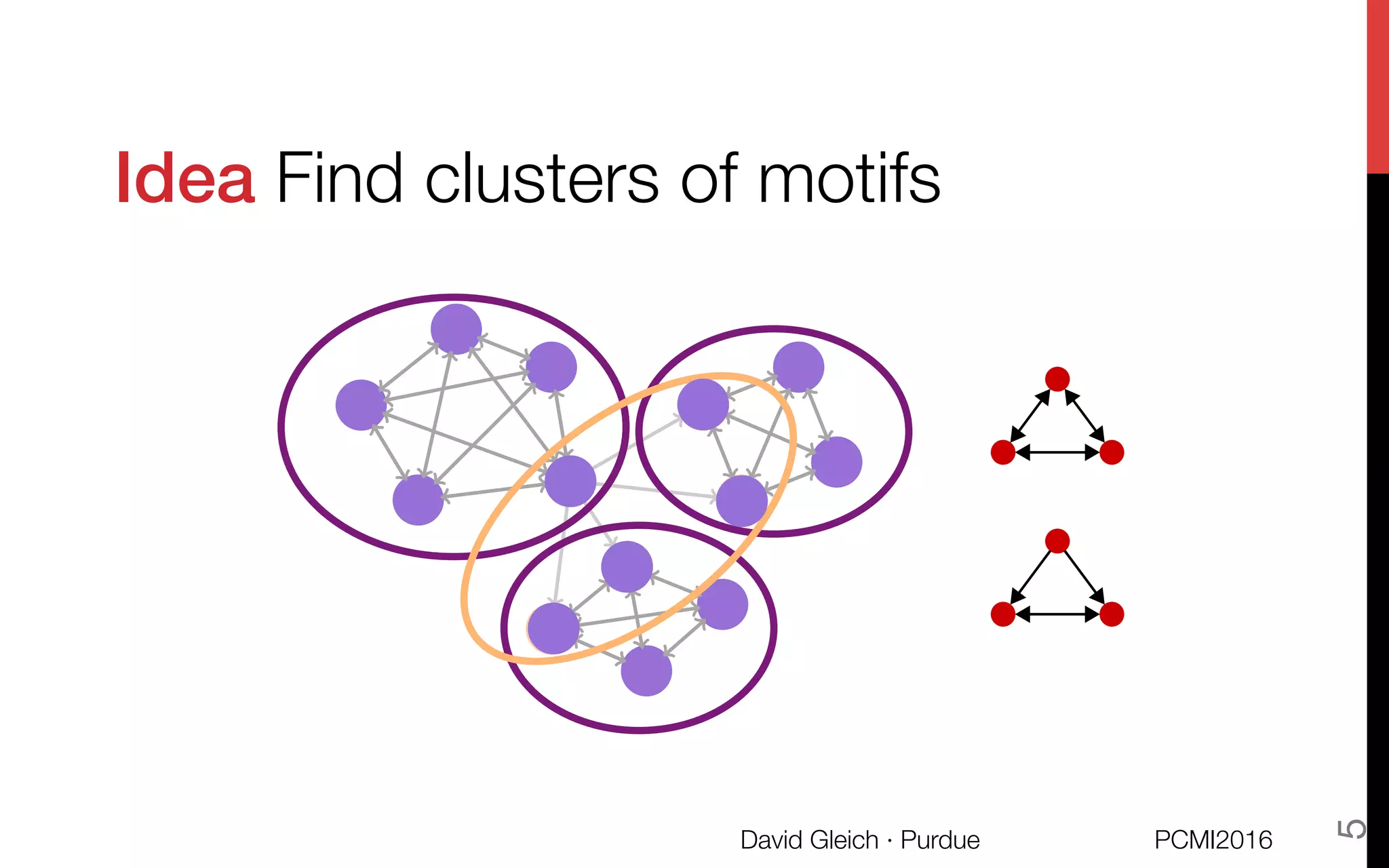
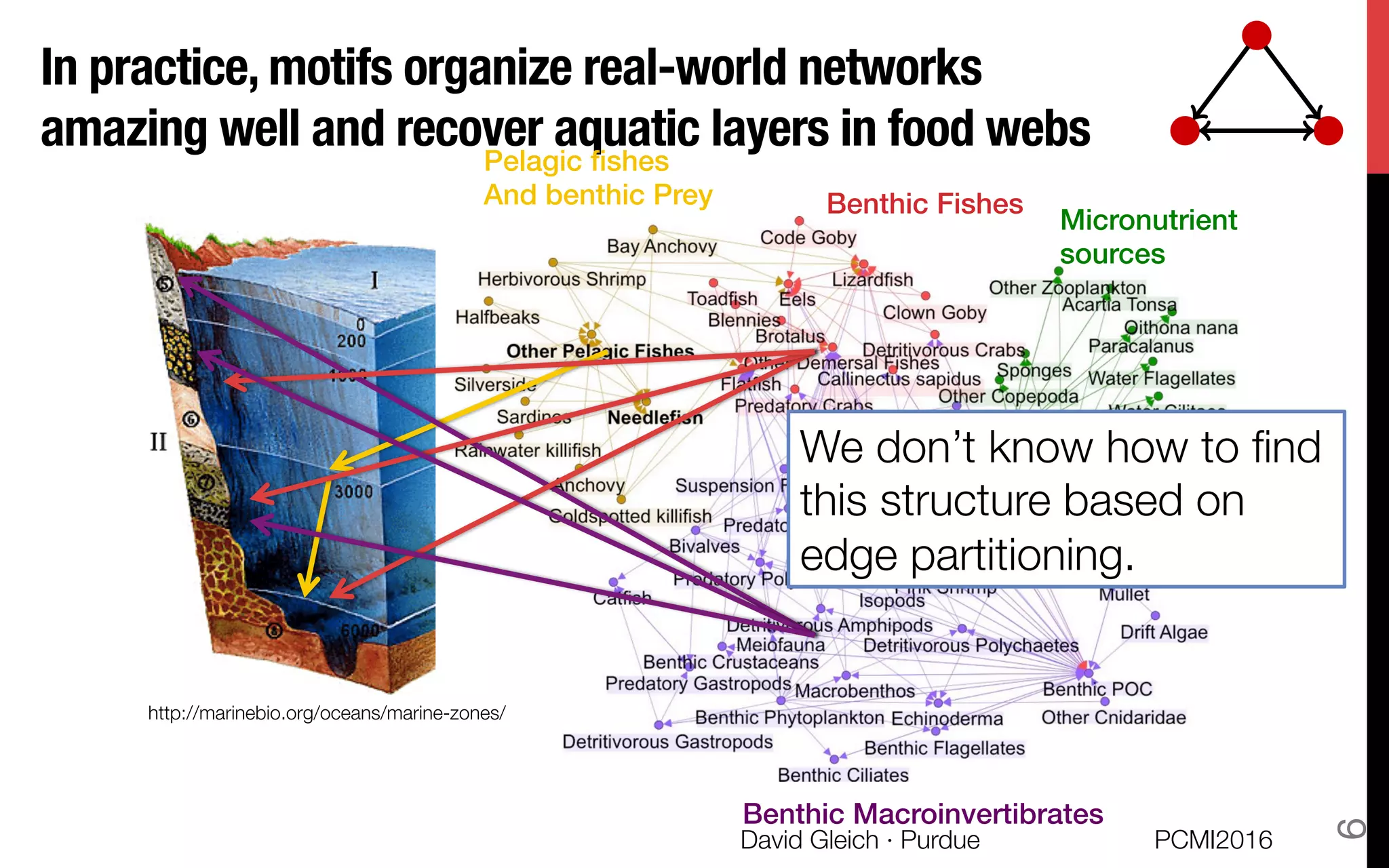
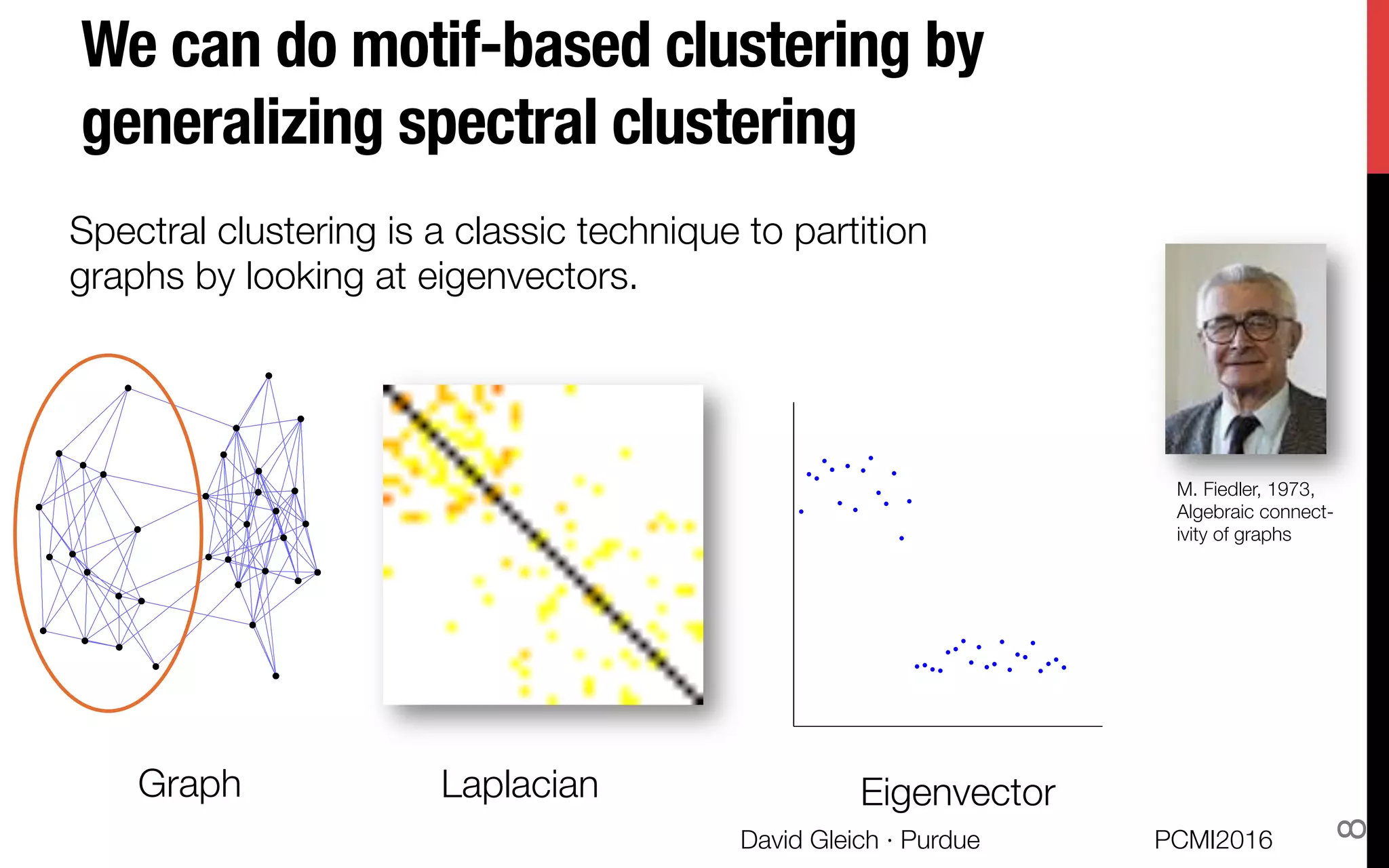
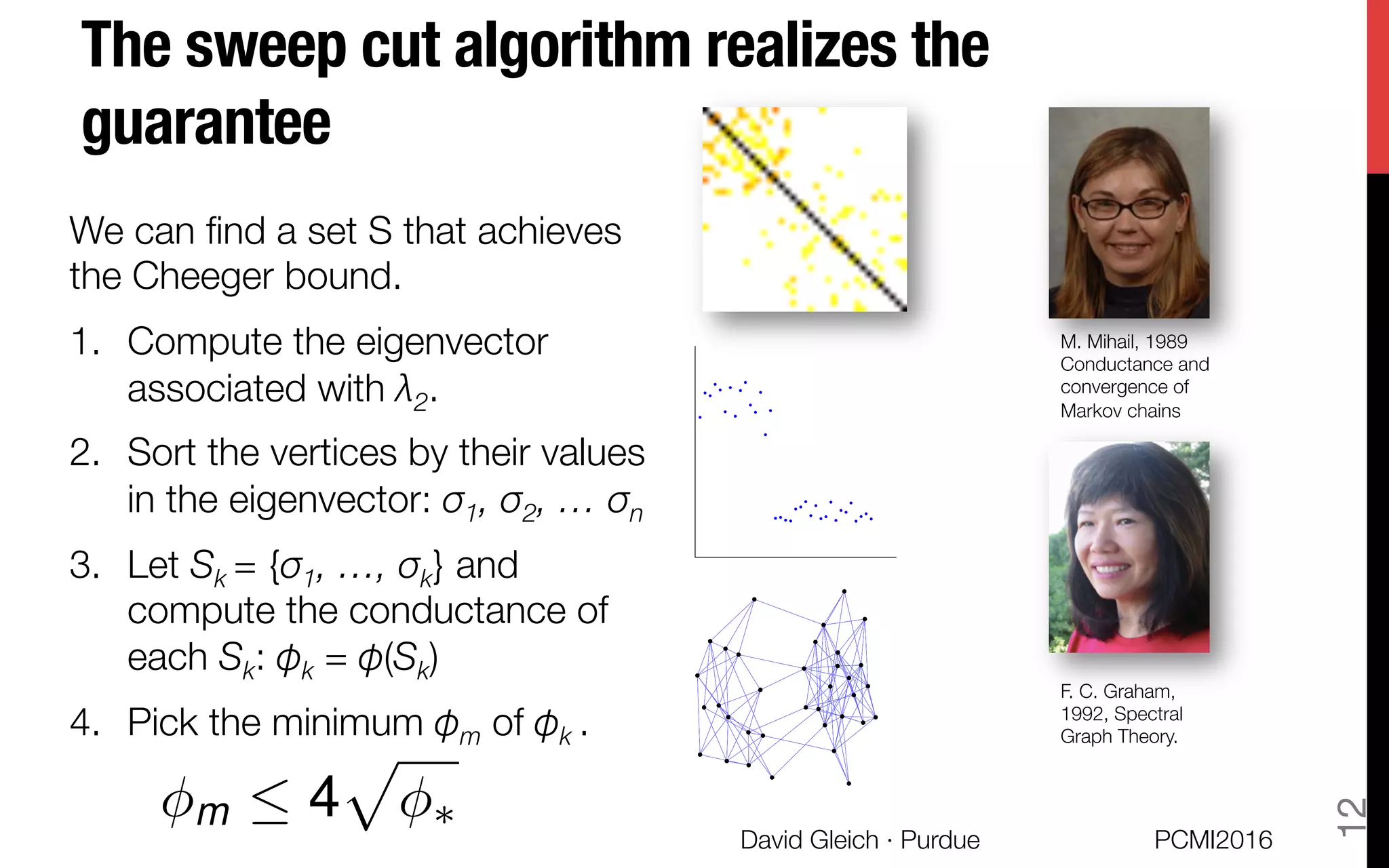
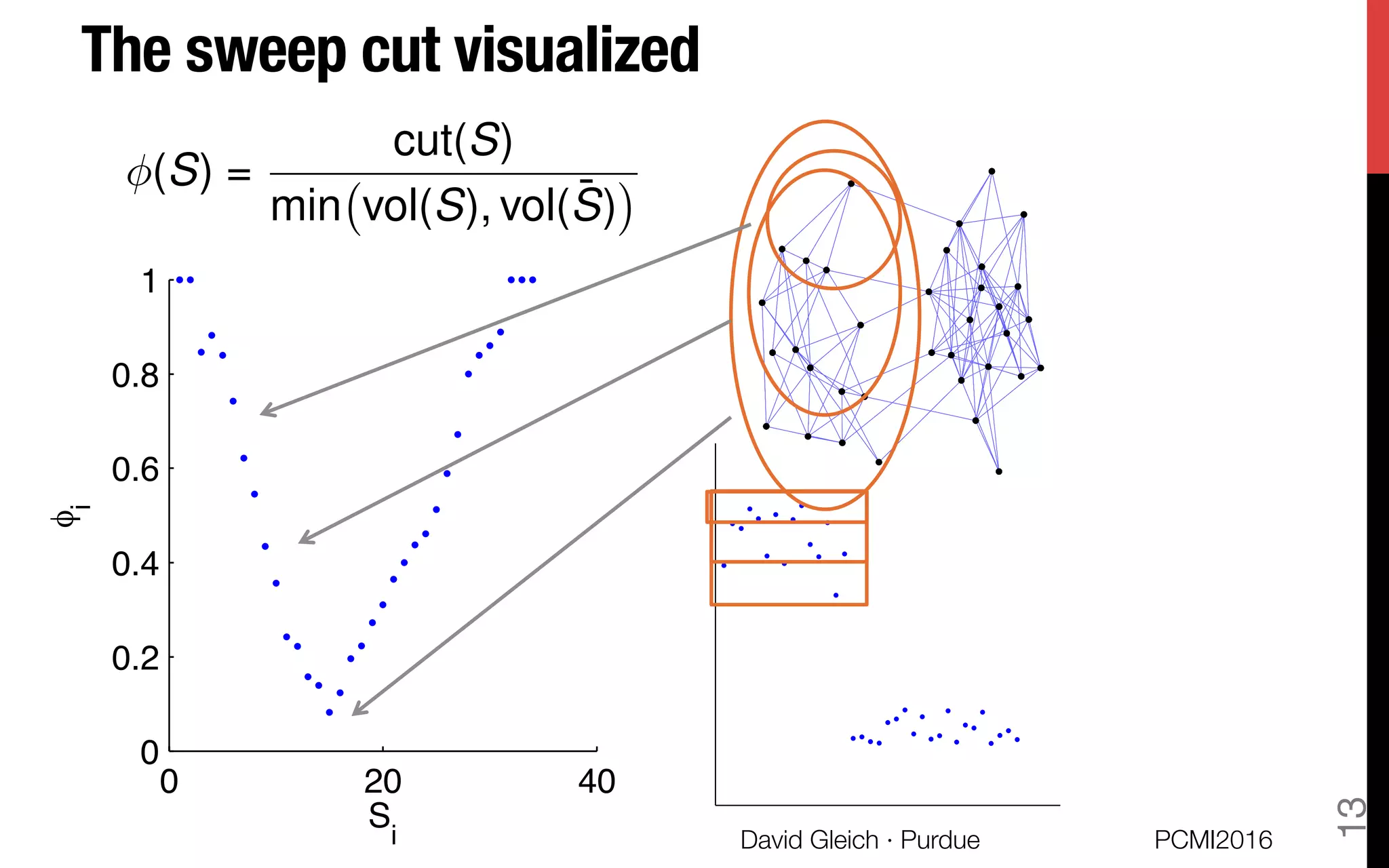
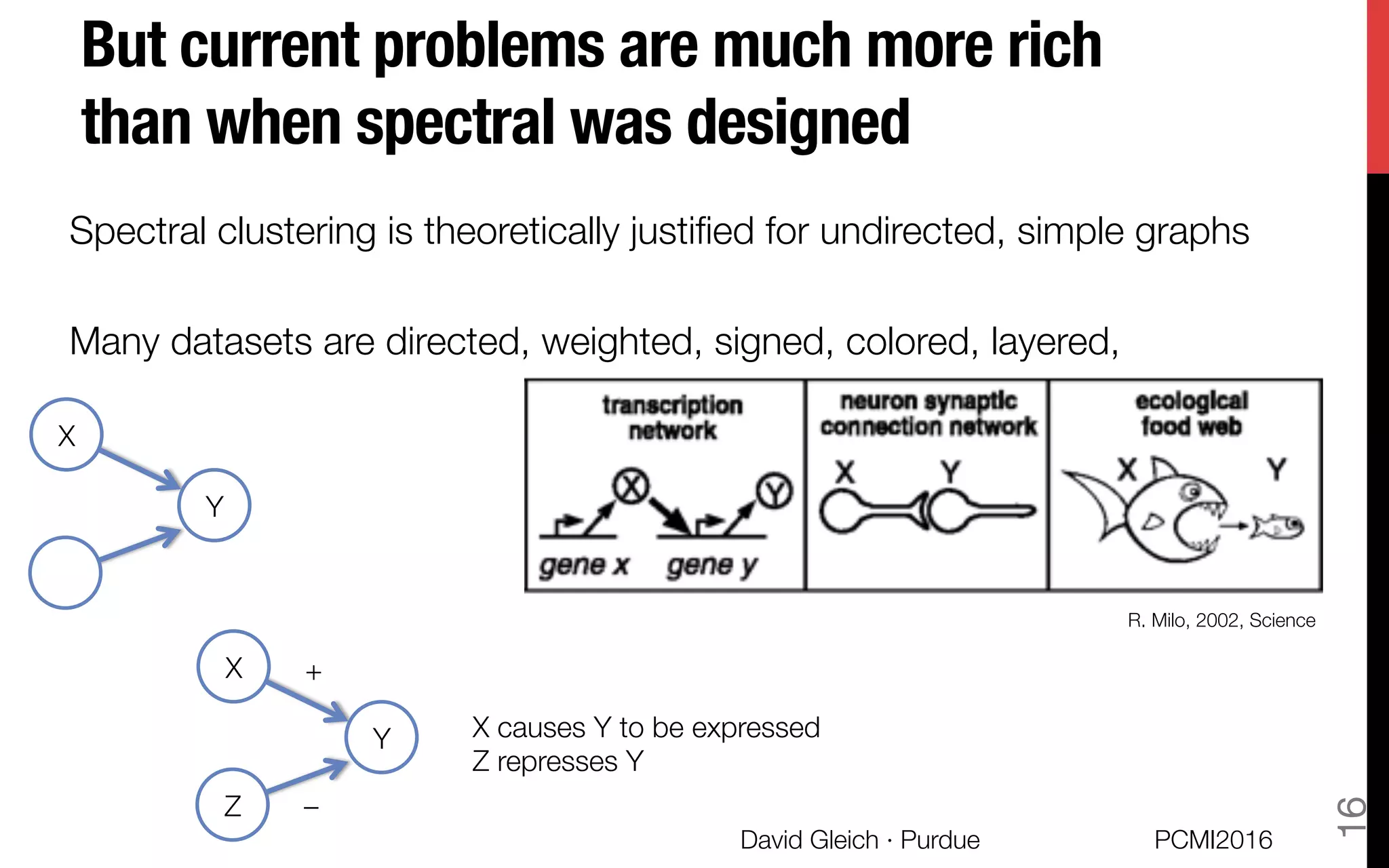
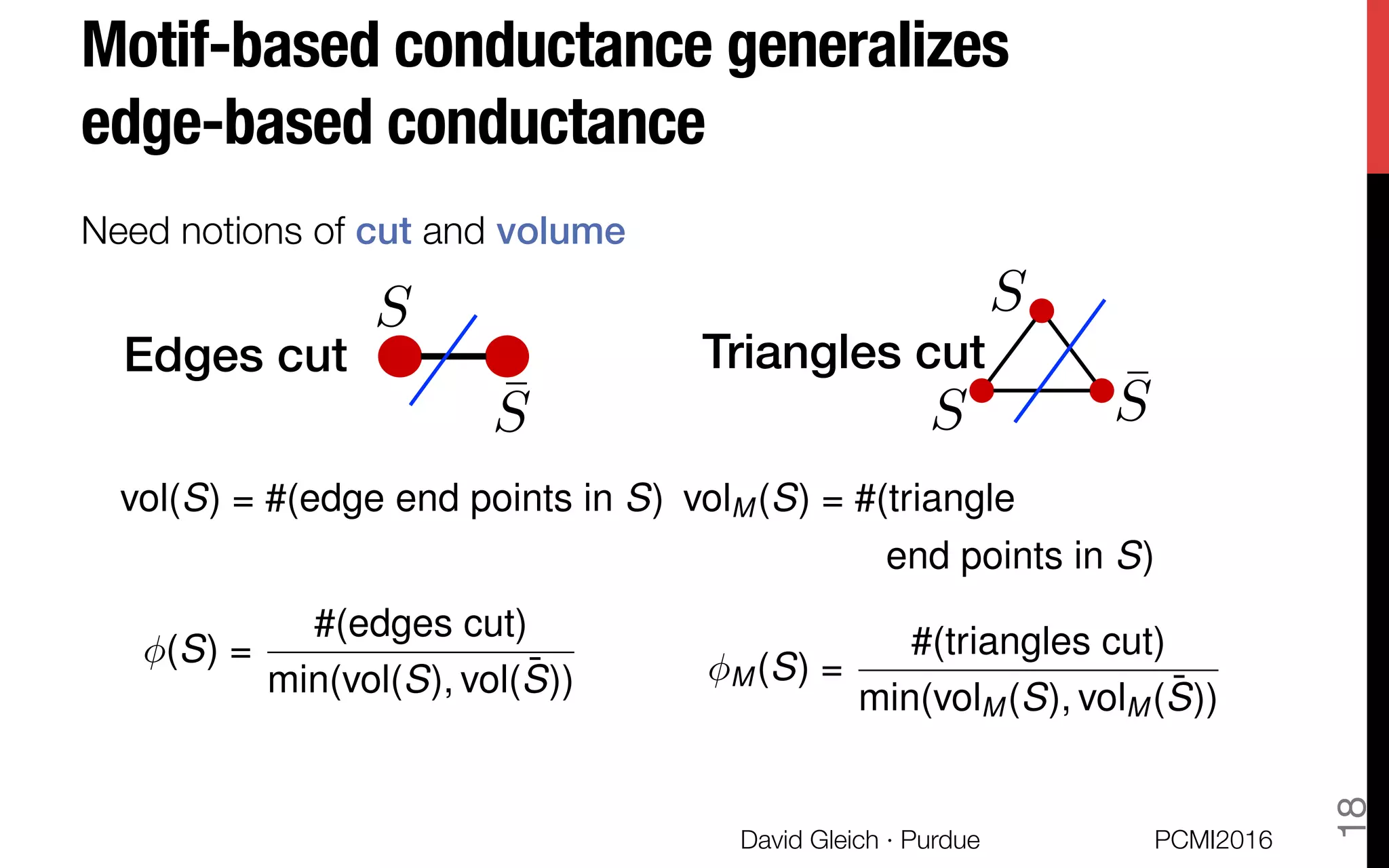
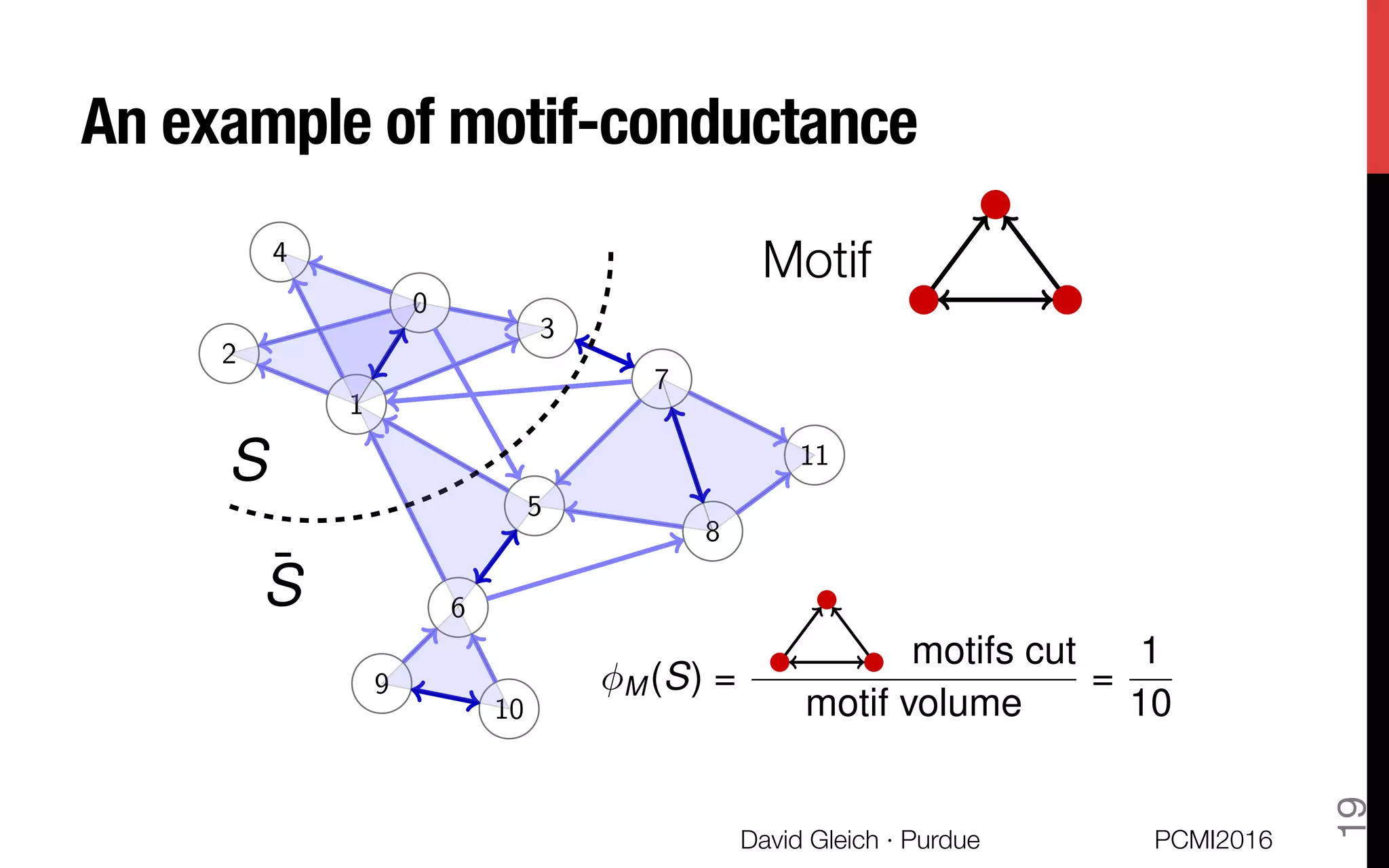
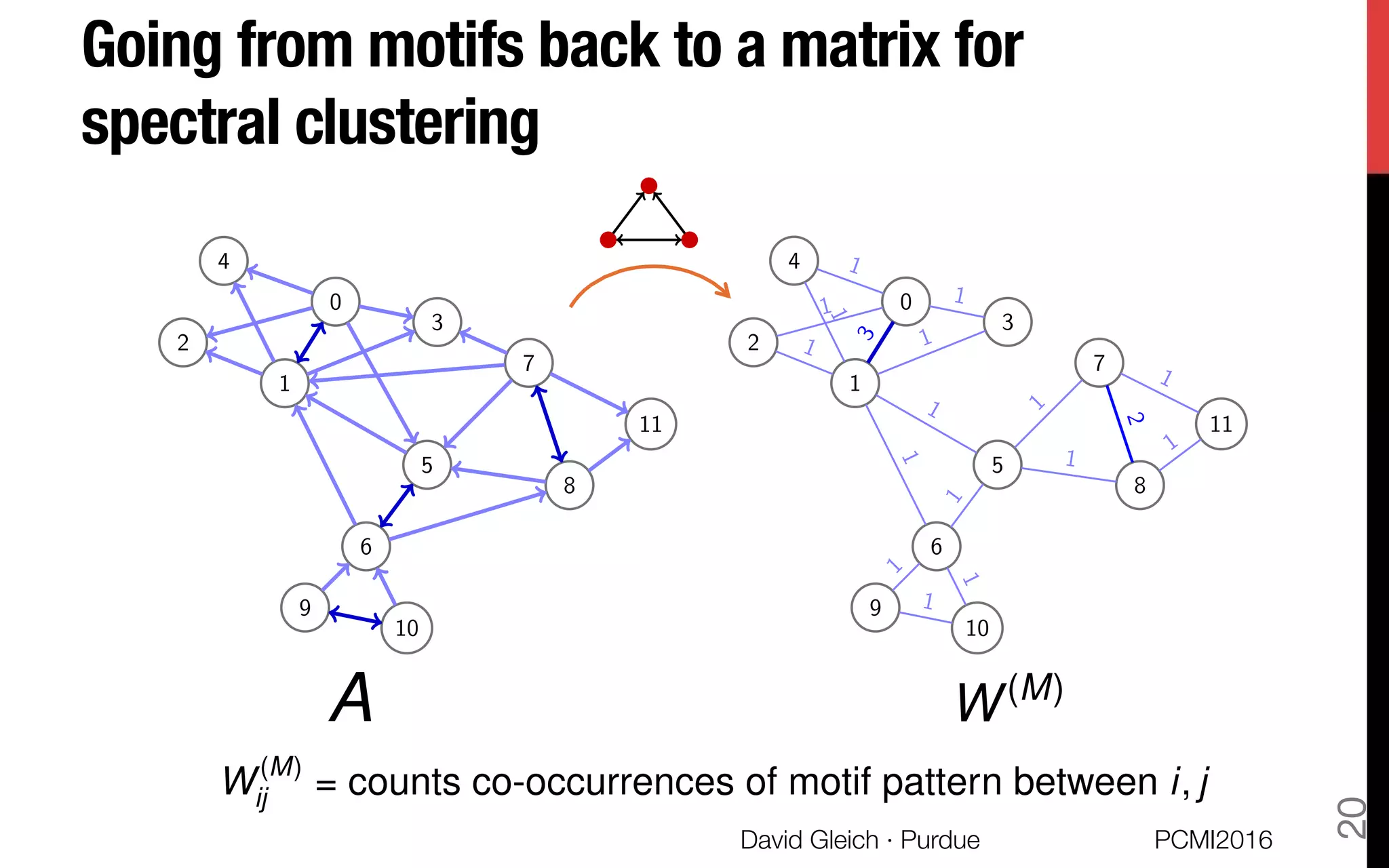
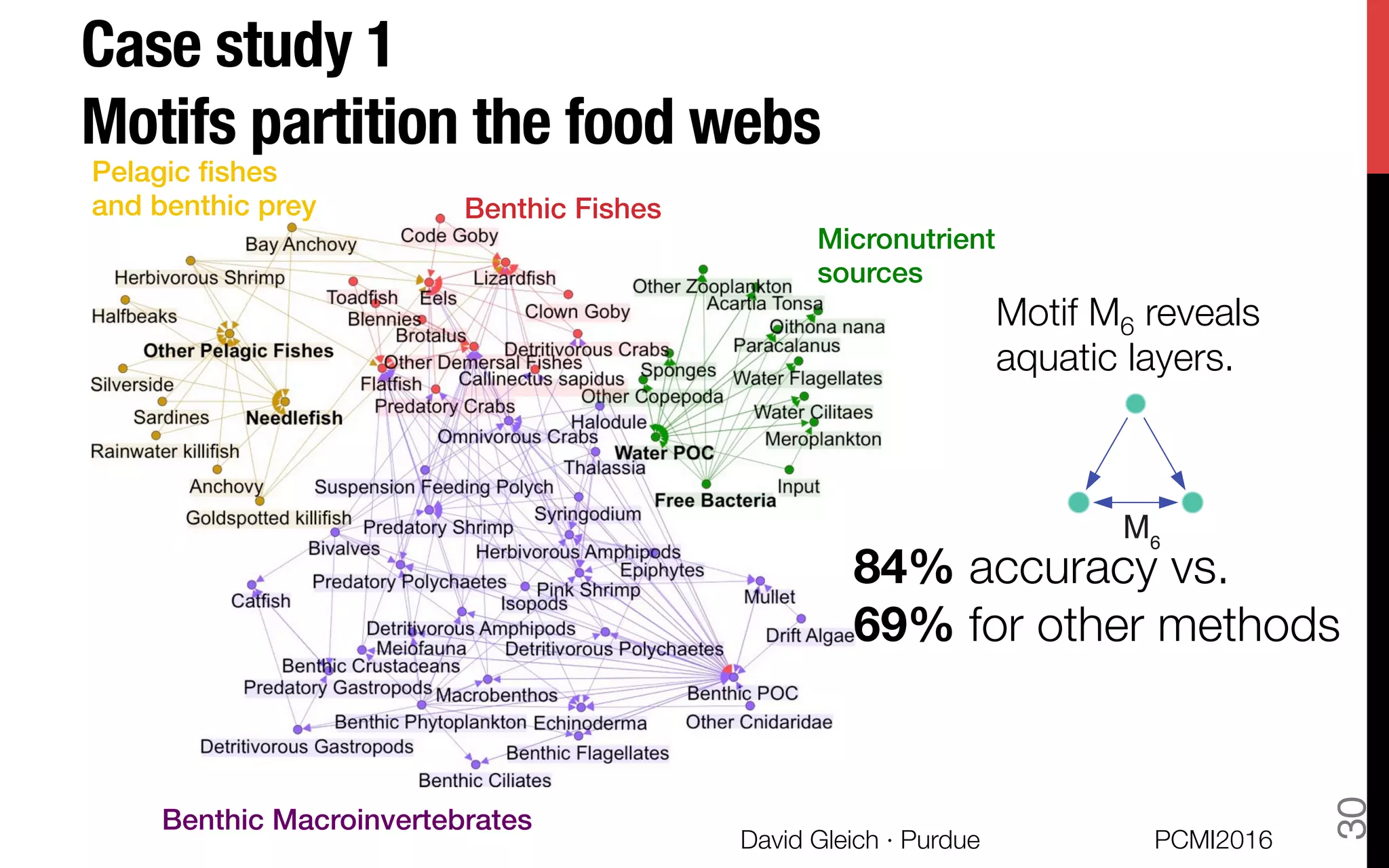
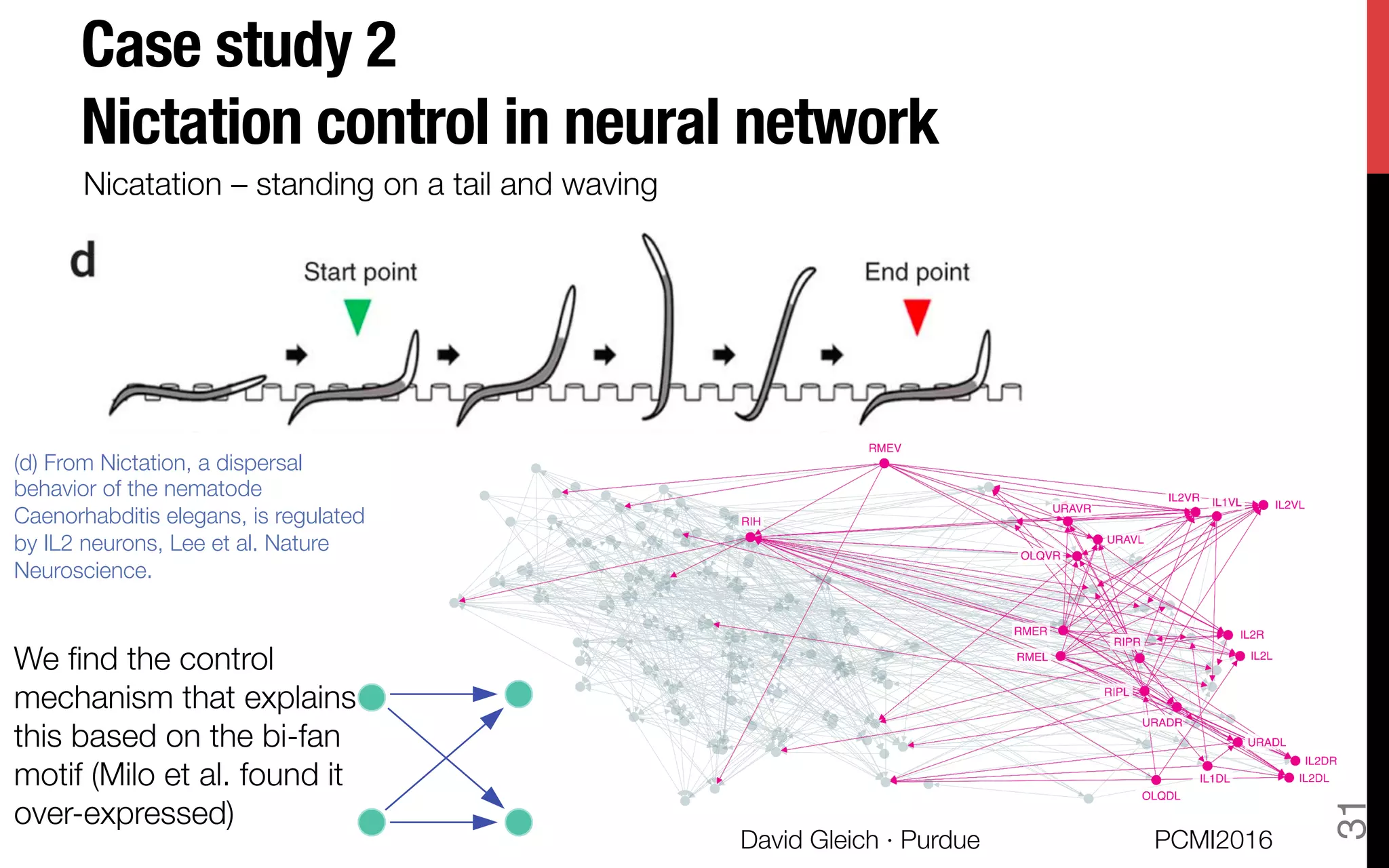
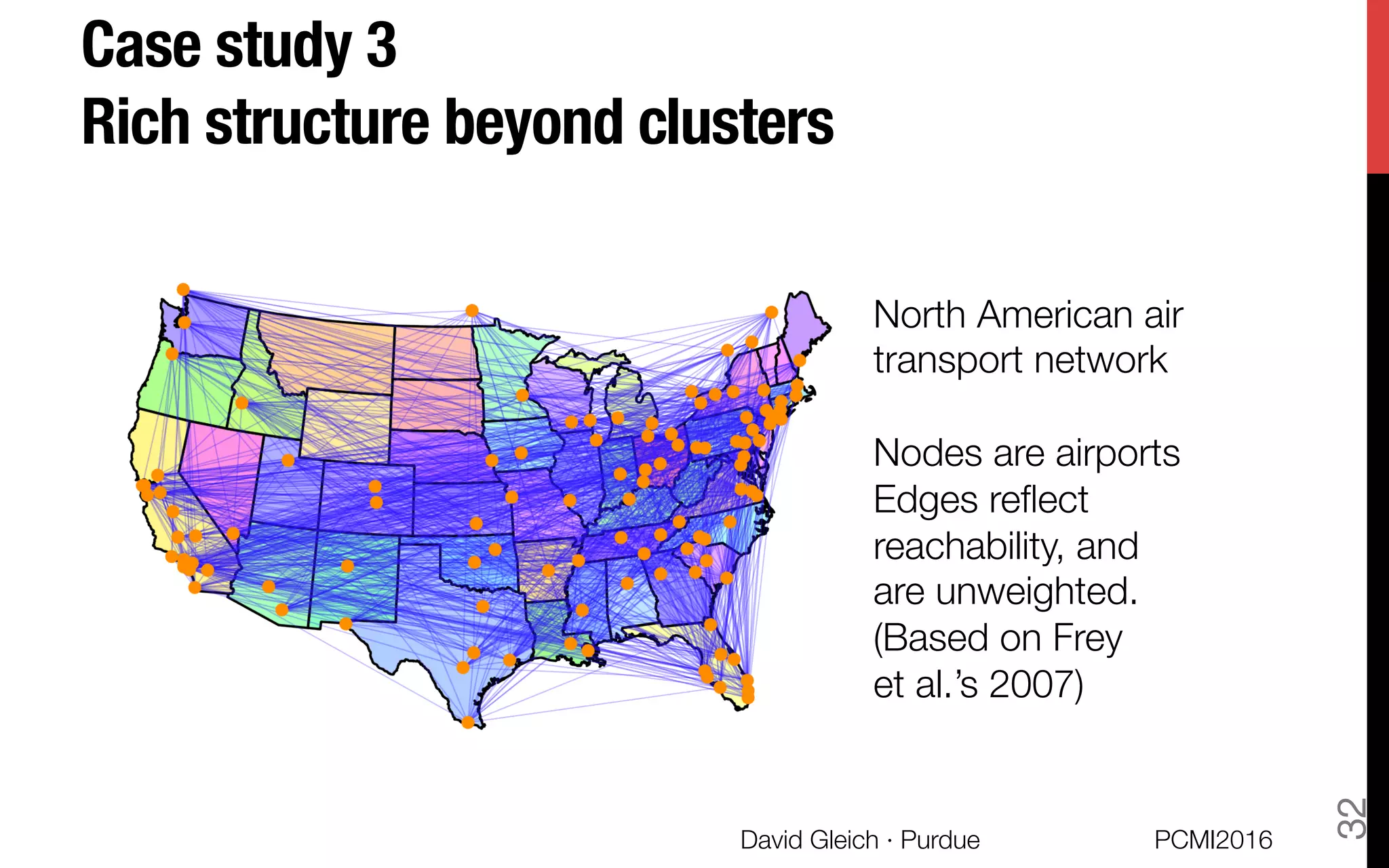
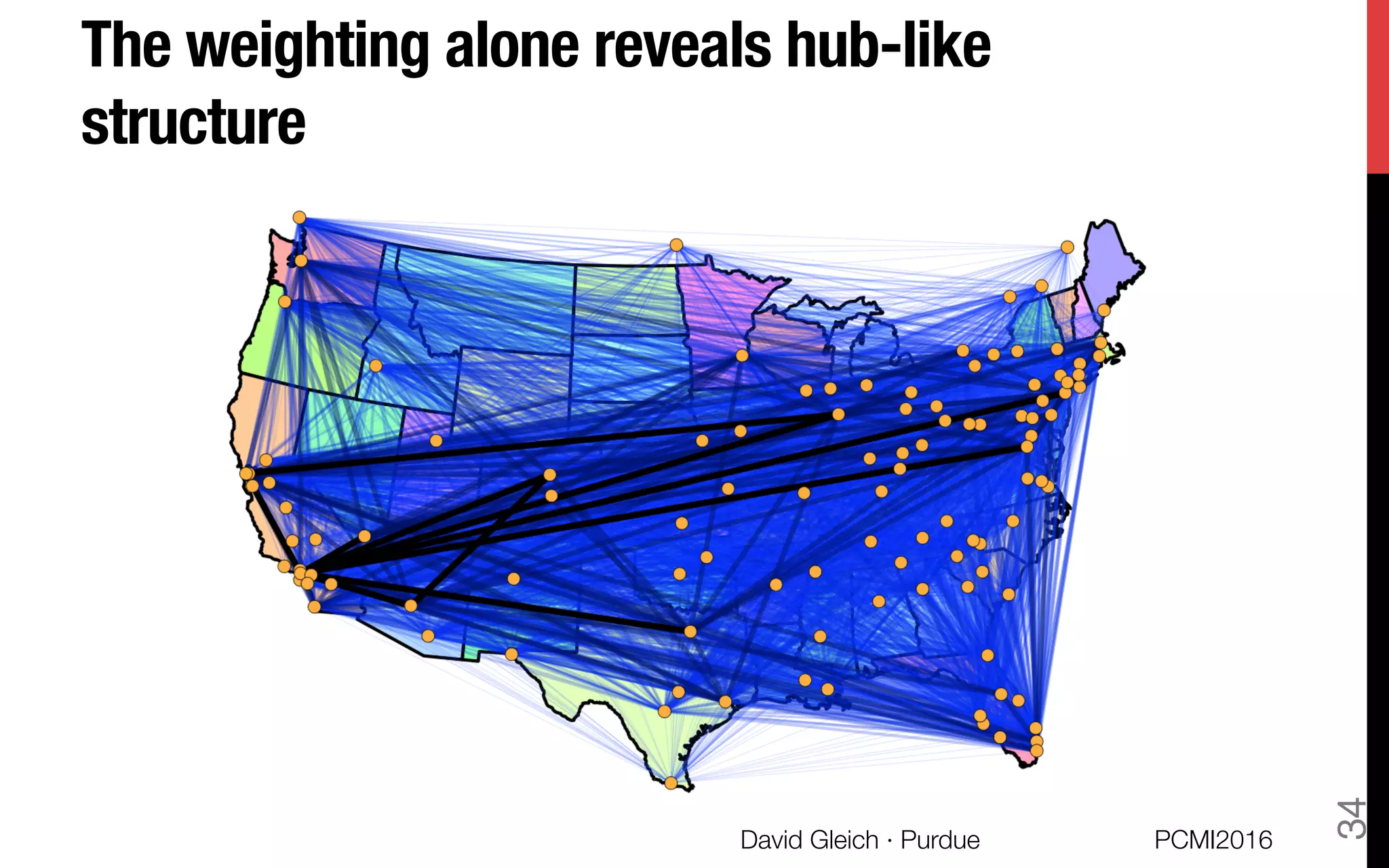
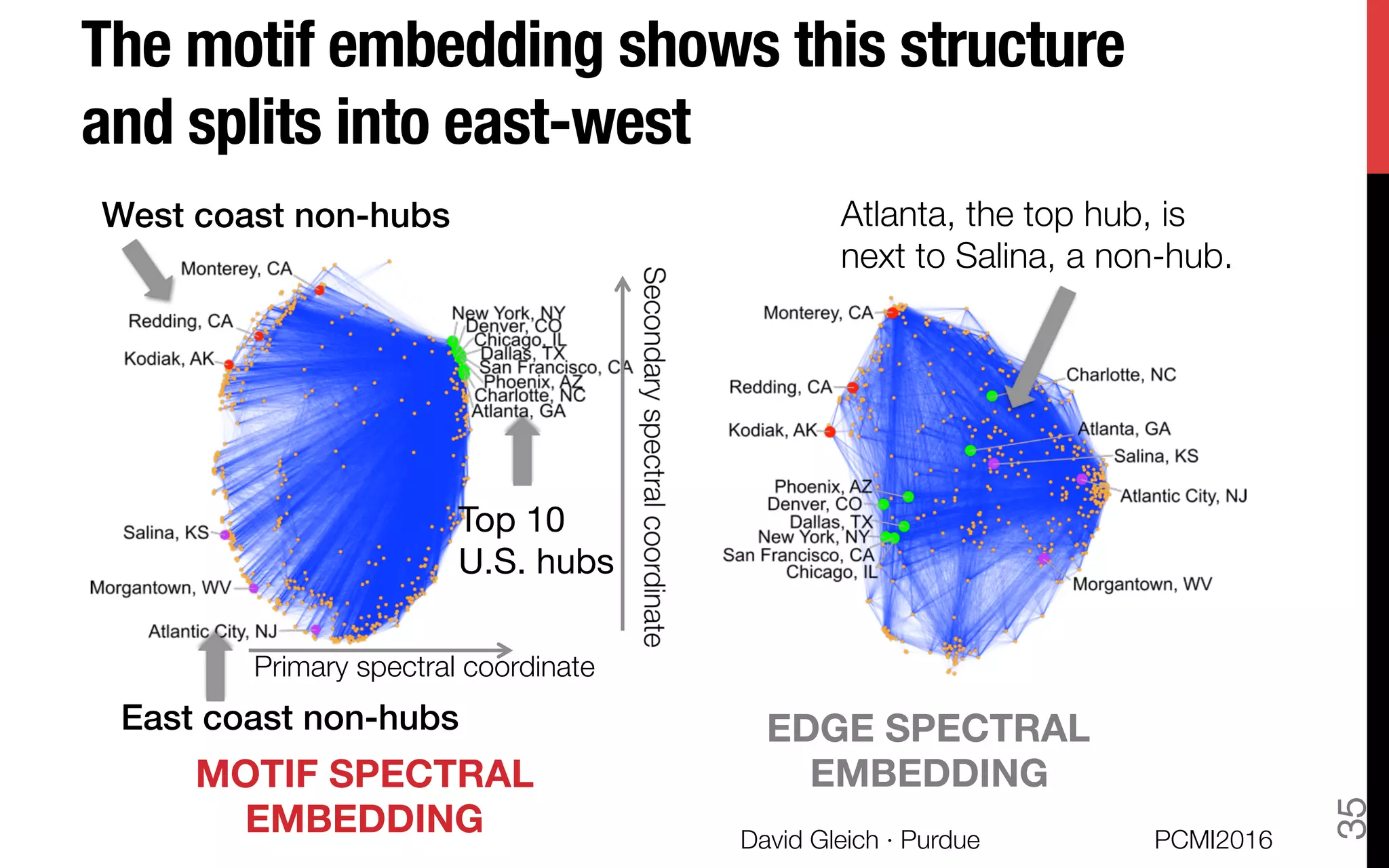
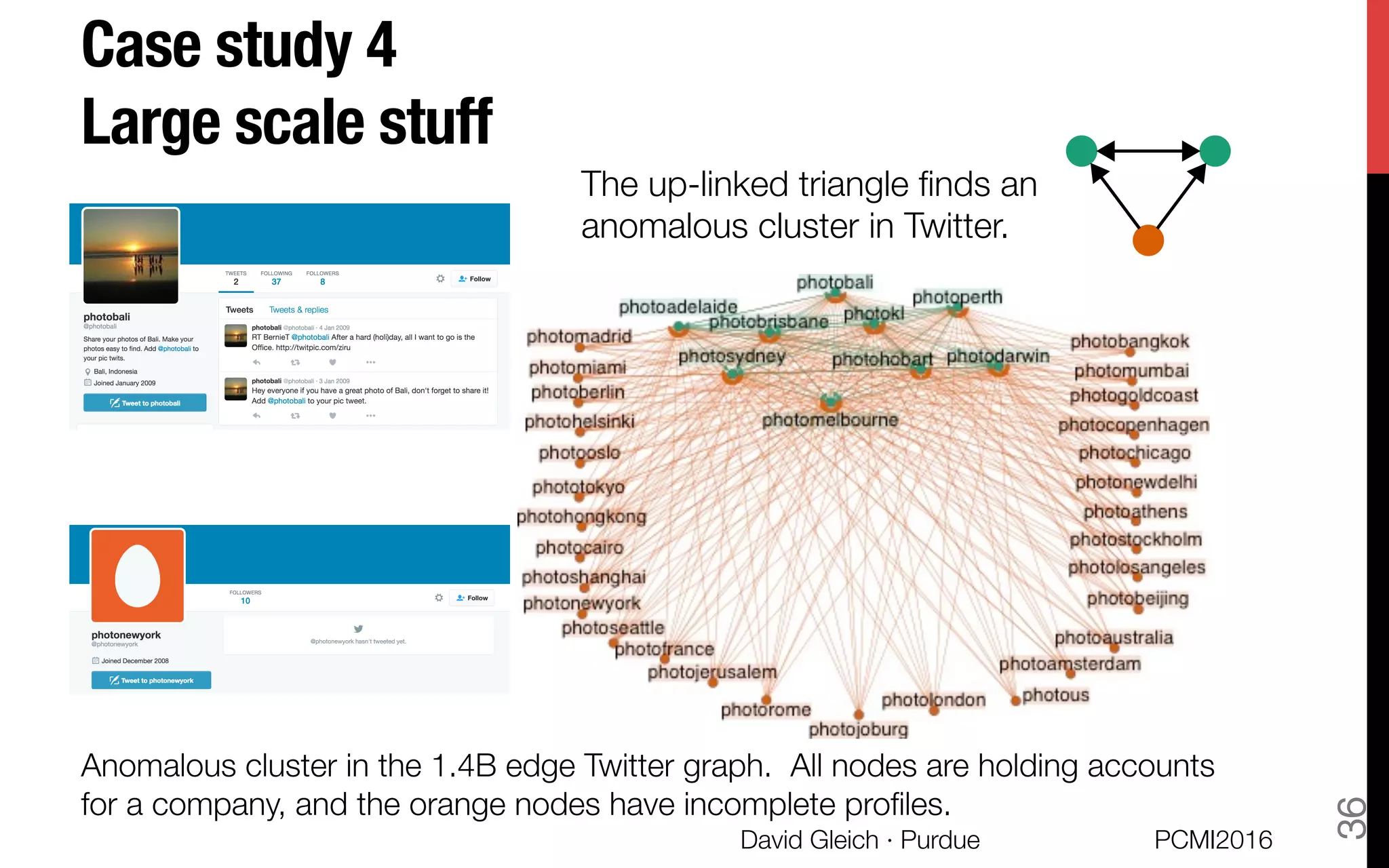
This document discusses the higher-order organization of complex networks, emphasizing motif-based clustering as an improvement over traditional edge-based community detection methods. It introduces a generalized conductance metric for motifs, a new spectral clustering algorithm, and presents case studies demonstrating the effectiveness of these methods in various applications, including aquatic ecosystems and neural networks. The work, led by David Gleich and collaborators, is supported by significant research funding and offers insights into analyzing complex systems with rich structures.

1. CEPDR
CEPVR
IL2R
OLLR
RIAL
RIAR
RIVL
RIVR
RMDDR
RMDL
RMDR
RMDVL
RMFL
SMDDL
SMDDR
SMDVR
URBR
Higher-order organization !
of complex networks
9
10
8
72
0
4
3
11
6
5
1
David F. Gleich!
Purdue University!
Joint work with "
Austin Benson and Jure
Leskovec, Stanford "
Supported by NSF CAREER
CCF-1149756, IIS-1422918
DARPA SIMPLEX
PCMI2016
David Gleich · Purdue
1
Code & Data snap.stanford.edu/higher-order"
github.com/arbenson/higher-order-organization-julia

2. Network analysis has two important
observations about real-world networks
Real-world networks have
modular organization!
Edge-based clustering and community
detection sometimes expose this
structure.
Control widgets are over-expressed
in complex networks. !
We can expose this motif or
graphlet analysis
PCMI2016
David Gleich · Purdue
2
Milo et al., Science, 2002.
Co-author network

3. Nodes and edges are not the fundamental
units of these networks.
Why should we look for structure "
in terms of them?
PCMI2016
David Gleich · Purdue
3

4. Idea Find clusters
PCMI2016
David Gleich · Purdue
4

5. Idea Find clusters of motifs
PCMI2016
David Gleich · Purdue
5

6. In practice, motifs organize real-world networks !
amazing well and recover aquatic layers in food webs
Micronutrient !
sources!
Benthic Fishes!
Benthic Macroinvertibrates!
Pelagic fishes !
And benthic Prey!
http://marinebio.org/oceans/marine-zones/
We don’t know how to find
this structure based on
edge partitioning.
PCMI2016
David Gleich · Purdue
6

7. Aside How did we get to this idea and looking
at this problem?
• Research is a journey.
PCMI2016
David Gleich · Purdue
7

8. We can do motif-based clustering by
generalizing spectral clustering
Spectral clustering is a classic technique to partition
graphs by looking at eigenvectors.
M. Fiedler, 1973,
Algebraic connect-
ivity of graphs
Graph
Laplacian
Eigenvector
PCMI2016
David Gleich · Purdue
8

9. Spectral clustering works based on
conductance
There are many ways to measure the quality of a set of
nodes of a graph to gauge how they partition the graph.
cut(S) = 7 cut( ¯S) = 7
|S| = 15 | ¯S| = 20
vol(S) = 85 vol( ¯S) = 151
cut(S) = 7 cut( ¯S) = 7
|S| = 15 | ¯S| = 20
vol(S) = 85 vol( ¯S) = 151
cut(S) = 7/85 + 7/151 = 0.1287
cut sparsity(S) = 7/15 = 0.4667
(S) = cond(S) = 7/85 = 0.0824
n
(S) = cut(S)/ min(vol(S), vol( ¯S))
PCMI2016
David Gleich · Purdue
9

10. Conductance sets in graphs
PCMI2016
David Gleich · Purdue
10
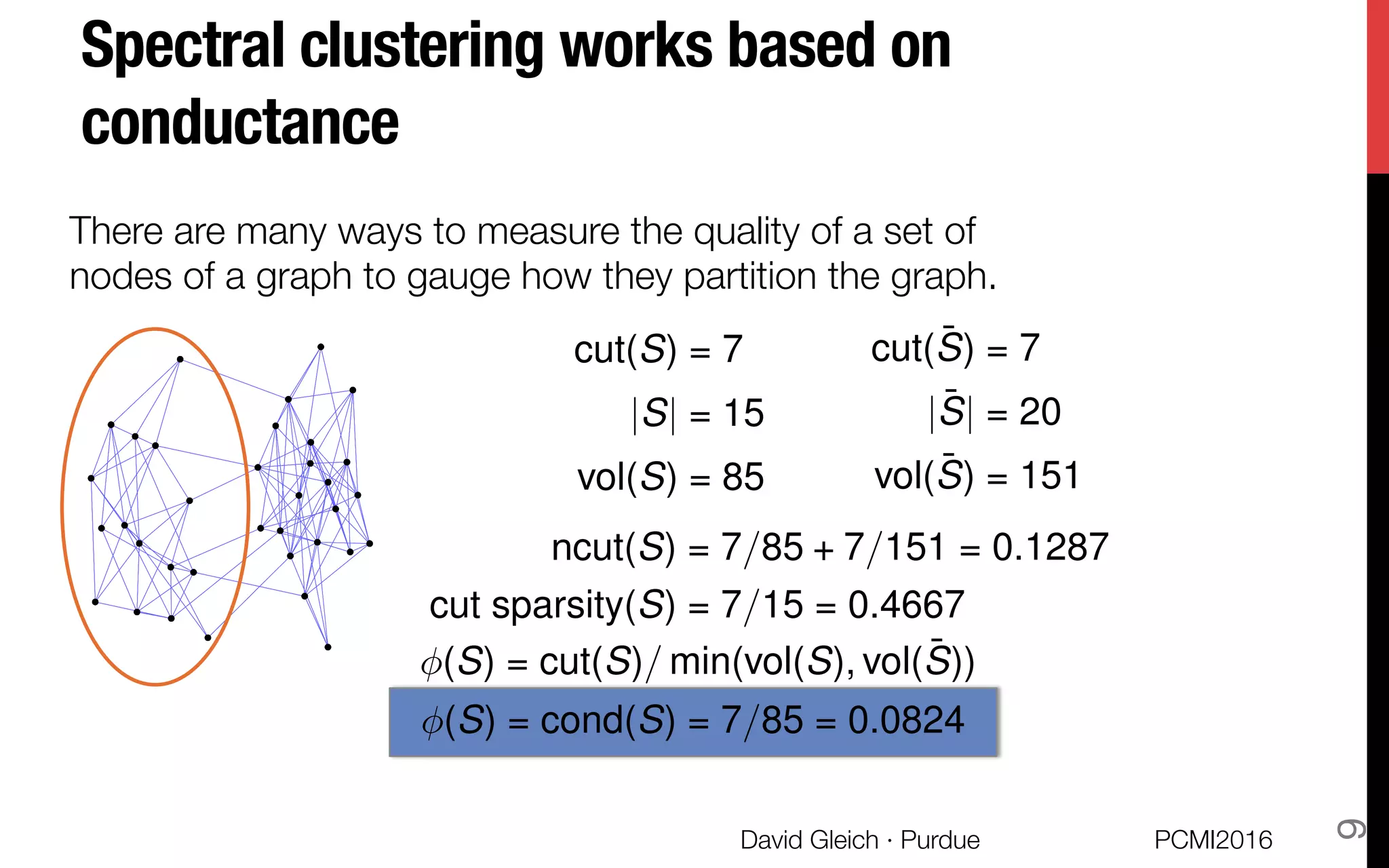
Conductance is one of the most important quality
scores [Schaeffer07]
used in Markov chain theory, bioinformatics, vision, etc.
PCMI Nelson showed how use you can this to get heavy-hitters in turnstile algs!
The conductance of a set of vertices is the ratio of
edges leaving to total edges:
Equivalently, it’s the probability that a random edge
leaves the set.
Small conductance ó Good set
(S) =
cut(S)
min vol(S), vol( ¯S)
(edges leaving the set)
(total edges
in the set)
cut(S) = 7
vol(S) = 33
vol( ¯S) = 11
(S) = 7/11

11. Spectral clustering has theoretical
guarantees
Cheeger Inequality
Finding the best conductance set
is NP-hard. L
• Cheeger realized the eigenvalues of the
Laplacian provided a bound in manifolds
• Alon and Milman independently realized
the same thing for a graph!
J. Cheeger, 1970,
A lower bound on
the smallest
eigenvalue of the
Laplacian
N. Alon, V. Milman
1985. λ1 isoperi-
metric inequalities
for graphs and
superconcentrators
Laplacian
2
⇤/2  2  2 ⇤
0 = 1  2  ...  n  2
Eigenvalues of the Laplacian
⇤ = set of smallest conductance
PCMI2016
David Gleich · Purdue
11

12. The sweep cut algorithm realizes the
guarantee
We can find a set S that achieves
the Cheeger bound.
1. Compute the eigenvector
associated with λ2.
2. Sort the vertices by their values
in the eigenvector: σ1, σ2, … σn
3. Let Sk = {σ1, …, σk} and
compute the conductance of
each Sk: φk = φ(Sk)
4. Pick the minimum φm of φk .
M. Mihail, 1989
Conductance and
convergence of
Markov chains
F. C. Graham,
1992, Spectral
Graph Theory.
m  4
p
⇤
PCMI2016
David Gleich · Purdue
12

13. The sweep cut visualized
0 20 40
0
0.2
0.4
0.6
0.8
1
S
i
φi
(S) =
cut(S)
min vol(S), vol( ¯S)
PCMI2016
David Gleich · Purdue
13

14. Demo…
PCMI2016
David Gleich · Purdue
14

15. That’s spectral clustering
40+ years of ideas and successful applications
• Fast algorithms that avoid eigenvectors "
(Graculus from Dhillon et al. 2007)
• Local algorithms for seeded detection"
(Spielman & Teng 2004; Andersen, Chung, Lang 2006)"
PCMI: Kimon gave a talk about this yesterday!
• Overlapping algorithms
• Embeddings
• And more!
PCMI2016
David Gleich · Purdue
15

16. But current problems are much more rich
than when spectral was designed
Spectral clustering is theoretically justified for undirected, simple graphs"
Many datasets are directed, weighted, signed, colored, layered,
R. Milo, 2002, Science
X
Y
X causes Y to be expressed
Z represses Y
X
Z
Y
+
–
PCMI2016
David Gleich · Purdue
16

17. Our contributions
1. A generalized conductance metric for motifs
2. A new spectral clustering algorithm to minimize the generalized
conductance.
3. AND an associated Cheeger inequality.
4. Aquatic layers in food webs
5. Control structures in neural networks
6. Hub structure in transportation networks
7. Anomaly detection in Twitter
Benson, Gleich, Leskovec, Science 2016.
PCMI2016
David Gleich · Purdue
17

18. Motif-based conductance generalizes !
edge-based conductance
Need notions of cut and volume!
(S) =
#(edges cut)
min(vol(S), vol( ¯S))
Edges cut! Triangles cut!
S S
S¯S ¯S
vol(S) = #(edge end points in S) volM (S) = #(triangle
end points in S)
M (S) =
#(triangles cut)
min(volM (S), volM ( ¯S))
PCMI2016
David Gleich · Purdue
18

19. An example of motif-conductance
9
10
6
5
8
1
7
2
0
4
3
11
9
10
8
7
2
0
4
3
11
6
5
1
¯S
S
Motif
M (S) =
motifs cut
motif volume
=
1
10
PCMI2016
David Gleich · Purdue
19

20. Going from motifs back to a matrix for
spectral clustering
9
10
6
5
8
1
7
2
0
4
3
11
9
10
6
5
8
1
7
2
0
4
3
11
1
1
1
1 1
1
1
1
1
1
1
1
1
1
1
1
2
3
A
W(M)
ij = counts co-occurrences of motif pattern between i, j
W(M)
PCMI2016
David Gleich · Purdue
20

21. Going from motifs back to a matrix for
spectral clustering
9
10
6
5
8
1
7
2
0
4
3
11
1
1
1
1 1
1
1
1
1
1
1
1
1
1
1
1
2
3
W(M)
ij = counts co-occurrences of motif pattern between i, j
W(M)
KEY INSIGHT!
Spectral clustering on
W(M) yields results on
the new motif notion
of conductance
M (S) =
motifs cut
motif volume
=
1
10
PCMI2016
David Gleich · Purdue
21

22. A motif-based clustering algorithm
1. Form weighted graph W(M)
2. Compute the Fiedler vector associated with λ2 of the
motif-normalized Laplacian
3. Run a (motif-cond) sweep cut on f!
9
10
6
5
8
1
7
2
0
4
3
11
1
1
1
1 1
1
1
1
1
1
1
1
1
1
1
1
2
3
W(M)
D = diag(W(M)
e)
L(M)
= D 1/2
(D W(M)
)D 1/2
L(M)
z = 2z
f(M)
= D 1/2
z
PCMI2016
David Gleich · Purdue
22

23. The sweep cut results
2 4 6 8 10
0
0.2
0.4
0.6
0.8
1
1
2
0
4
3
1
2
0
4
3
9
10
6
Best higher-
order cluster
2nd best higher-
order cluster
9
10
6
5
8
1
7
2
0
4
3
11
1
1
1
1 1
1
1
1
1
1
1
1
1
1
1
1
2
3
(Order from the Fiedler vector)
PCMI2016
David Gleich · Purdue
23

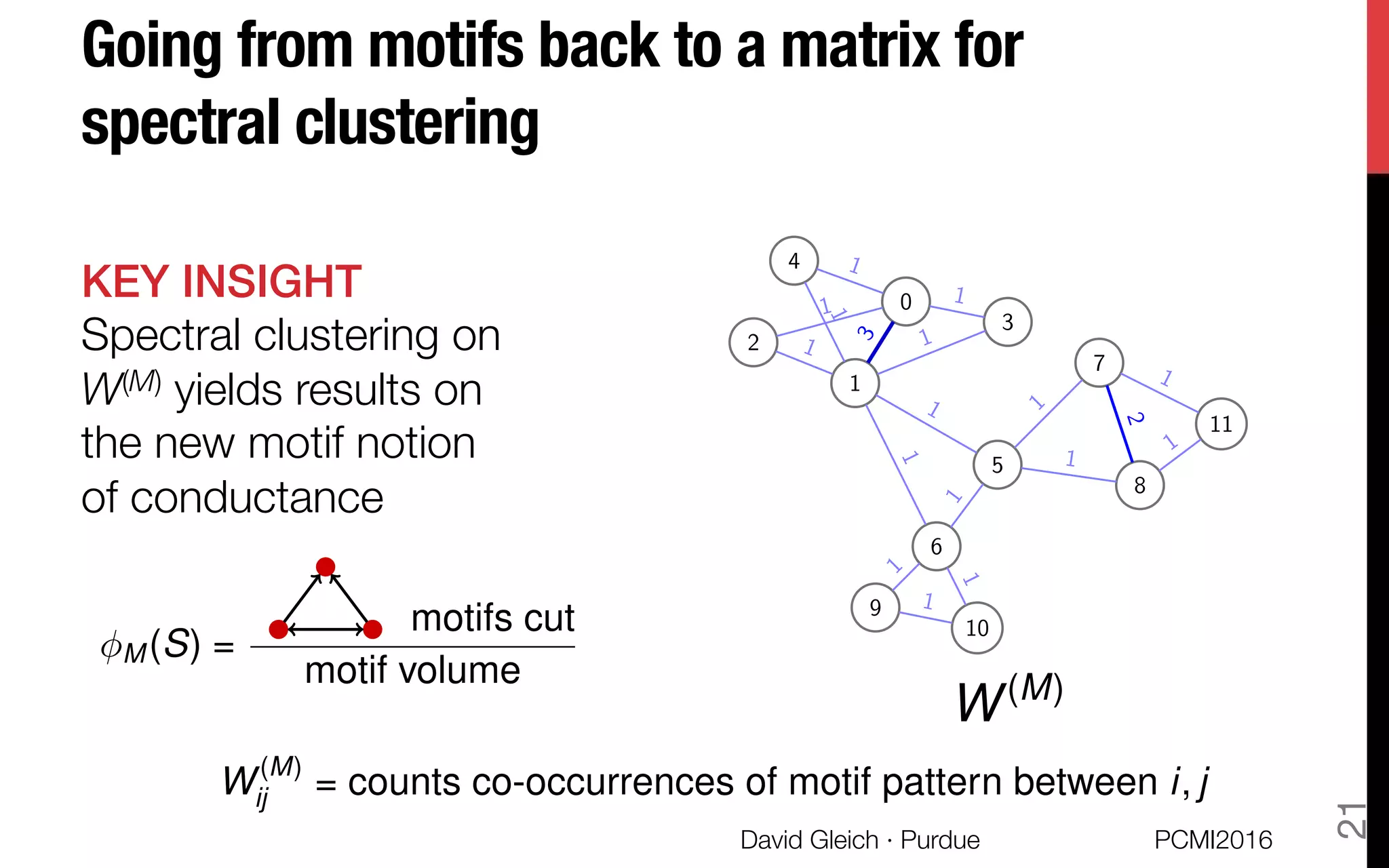
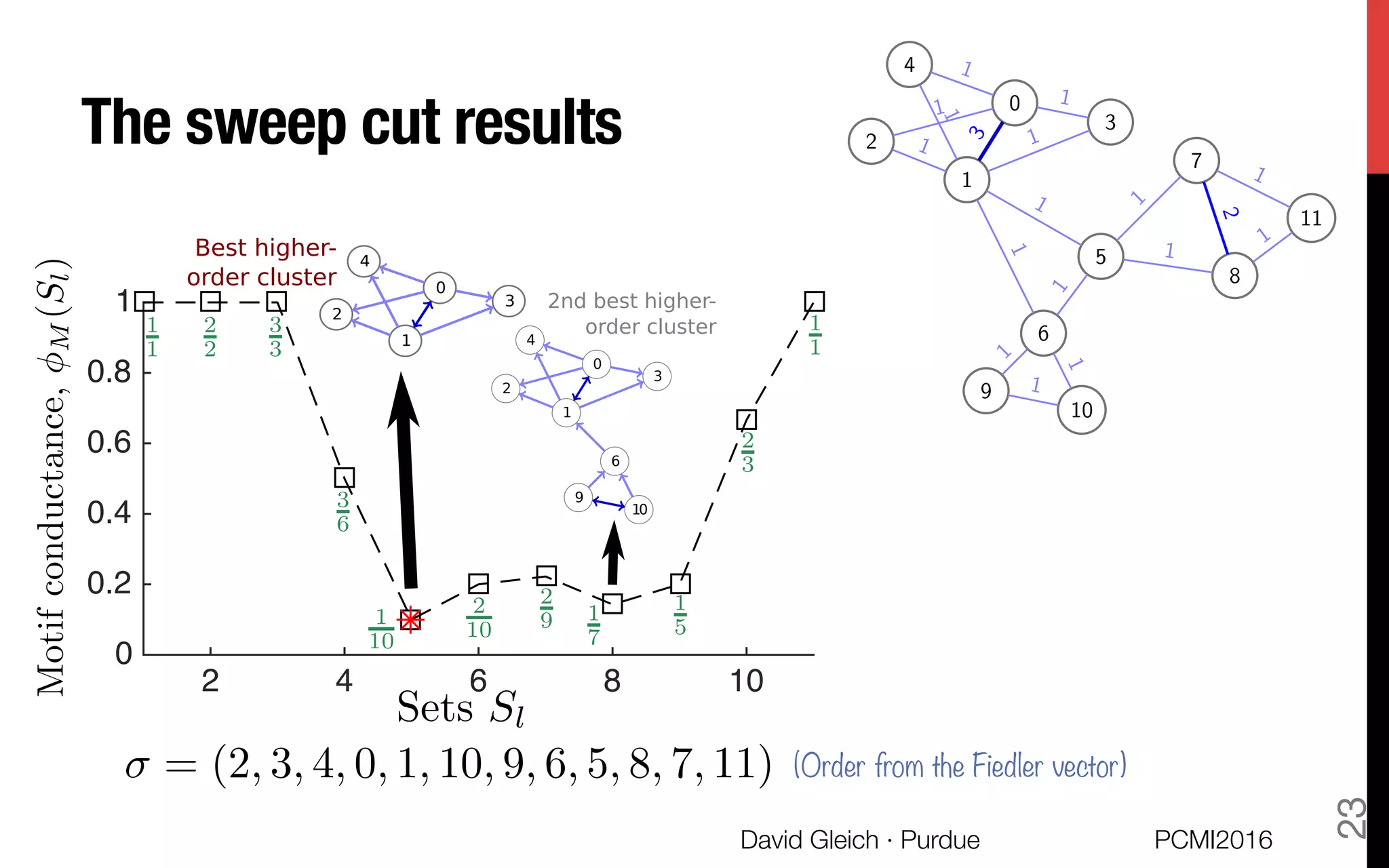
24. The motif-based Cheeger inequality
THEOREM!
If the motif has three nodes, then the sweep procedure
on the weighted graph finds a set S of nodes for which
THEOREM For more than 4 nodes, we "
use a slightly altered conductance.
M (S)  4
q
⇤
M
cutM (S, G) =
X
{i,j,k}2M(G)
Indicator[xi , xj , xk not the same]
= quadratic in x
M(G) = {instances of M in G}
Key Proof Step!
PCMI2016
David Gleich · Purdue
24

25. Awesome advantages
We inherit 40+ years of research!
• Fast algorithms "
(ARPACK, etc.)!
• Local methods!
• Overlapping!
• Easy to implement "
(20 lines of Matlab/Julia)
• Scalable (1.4B edges graphs "
are not a prob.)
PCMI2016
David Gleich · Purdue
25
12/13/2015 motif_example
function [S, conductances] = MotifClusterM36(A)
B = spones(A & A'); % bidirectional links
U = A - B; % unidirectional links
W = (B * U') .* U' + (U * B) .* U + (U' * U) .* B; % Motif M_3^6
D = diag(sum(W));
Ln = speye(size(W, 1)) - sqrt(D)^(-1) * W * sqrt(D)^(-1);
[Z, ~] = eigs(Ln, 2, 'sm');
[~, order] = sort(sqrt(D)^(-1) * Z(:, 2));
conductances = zeros(n, 1);
x = zeros(n, 1);
for i = 1:n
x(order(i)) = 1;
xn = ~x + 0;
conductances(i) = x' * (D - W) * x / min(x' * D * x, xn' * D * xn);
end
[~, split] = min(conductances);
S = order(1:split);
Error using motif_example (line 2)
Not enough input arguments.
Published with MATLAB® R2015a

26. Case studies
An intro note!
1. Aquatic layers in food webs."
Signed patterns in regulatory networks
2. Control structures in neural networks
3. Hub structure in transportation networks.
4. Scaling and large data
PCMI2016
David Gleich · Purdue
26

27. NOTE !
The partition depends on the motif
10
11
9
8
3
1
5
4
12
7
6
2
10
11
9
8
3
1
5
4
12
7
6
2
PCMI2016
David Gleich · Purdue
27

28. Case study 1!
Motifs partition the food webs
Food webs model
energy exchange
in species of an
ecosystem
i -> j
means i’s energy
goes to j "
(or j eats i)
Via Cheeger, motif
conductance is
better than edge
conductance.
PCMI2016
David Gleich · Purdue
28

29. Demo
PCMI2016
David Gleich · Purdue
29

30. Case study 1!
Motifs partition the food webs
Micronutrient !
sources!
Benthic Fishes!
Benthic Macroinvertebrates!
Pelagic fishes !
and benthic prey!
Motif M6 reveals
aquatic layers.
A
84% accuracy vs.
69% for other methods
PCMI2016
David Gleich · Purdue
30

31. Case study 2!
Nictation control in neural network
(d) From Nictation, a dispersal
behavior of the nematode
Caenorhabditis elegans, is regulated
by IL2 neurons, Lee et al. Nature
Neuroscience.
"
We find the control
mechanism that explains
this based on the bi-fan
motif (Milo et al. found it
over-expressed)
A B
C
Nicatation – standing on a tail and waving
A B
PCMI2016
David Gleich · Purdue
31

32. Case study 3 !
Rich structure beyond clusters
North American air "
transport network
Nodes are airports
Edges reflect "
reachability, and "
are unweighted.
(Based on Frey"
et al.’s 2007)
PCMI2016
David Gleich · Purdue
32

33. We can use complex motifs with non-
anchored nodes
D
C
B
A
Counts length-two walks
PCMI2016
David Gleich · Purdue
33

34. The weighting alone reveals hub-like
structure
PCMI2016
David Gleich · Purdue
34

35. The motif embedding shows this structure
and splits into east-west
Top 10
U.S. hubs
East coast non-hubs!
West coast non-hubs!
Primary spectral coordinate
Atlanta, the top hub, is
next to Salina, a non-hub.
MOTIF SPECTRAL
EMBEDDING
EDGE SPECTRAL
EMBEDDING
PCMI2016
David Gleich · Purdue
35

36. Case study 4!
Large scale stuff
The up-linked triangle finds an
anomalous cluster in Twitter.
Anomalous cluster in the 1.4B edge Twitter graph. All nodes are holding accounts
for a company, and the orange nodes have incomplete profiles.
PCMI2016
David Gleich · Purdue
36

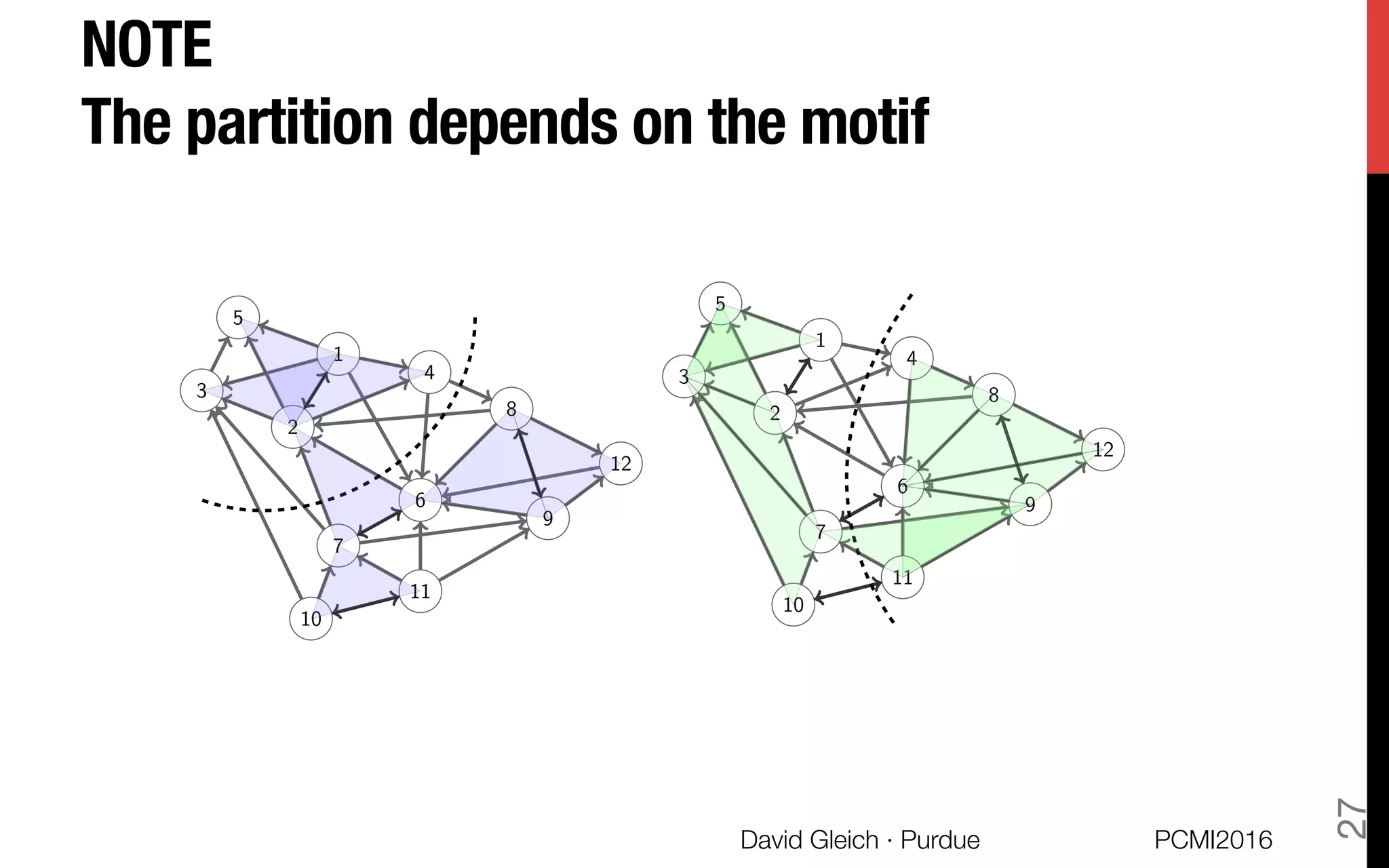
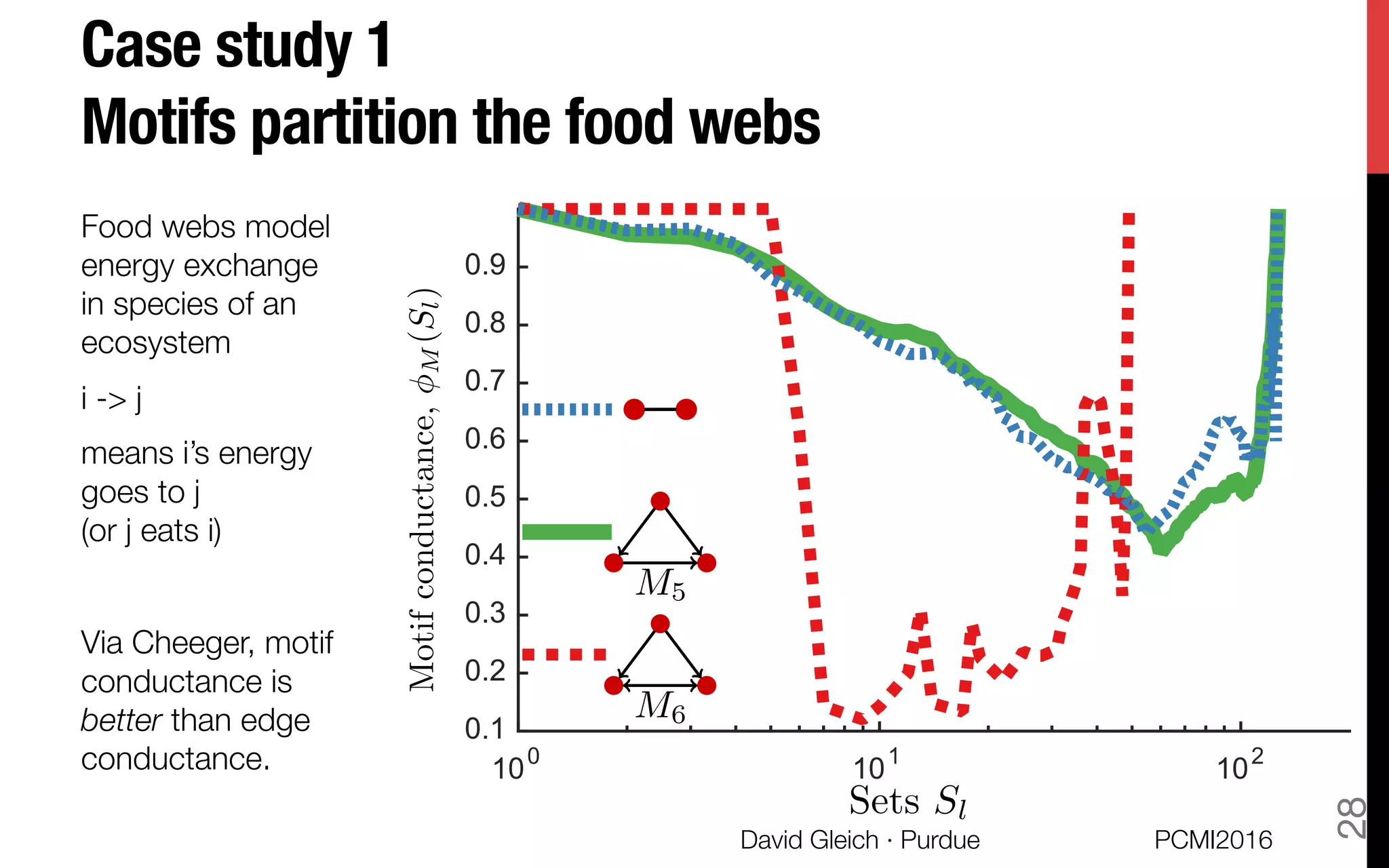
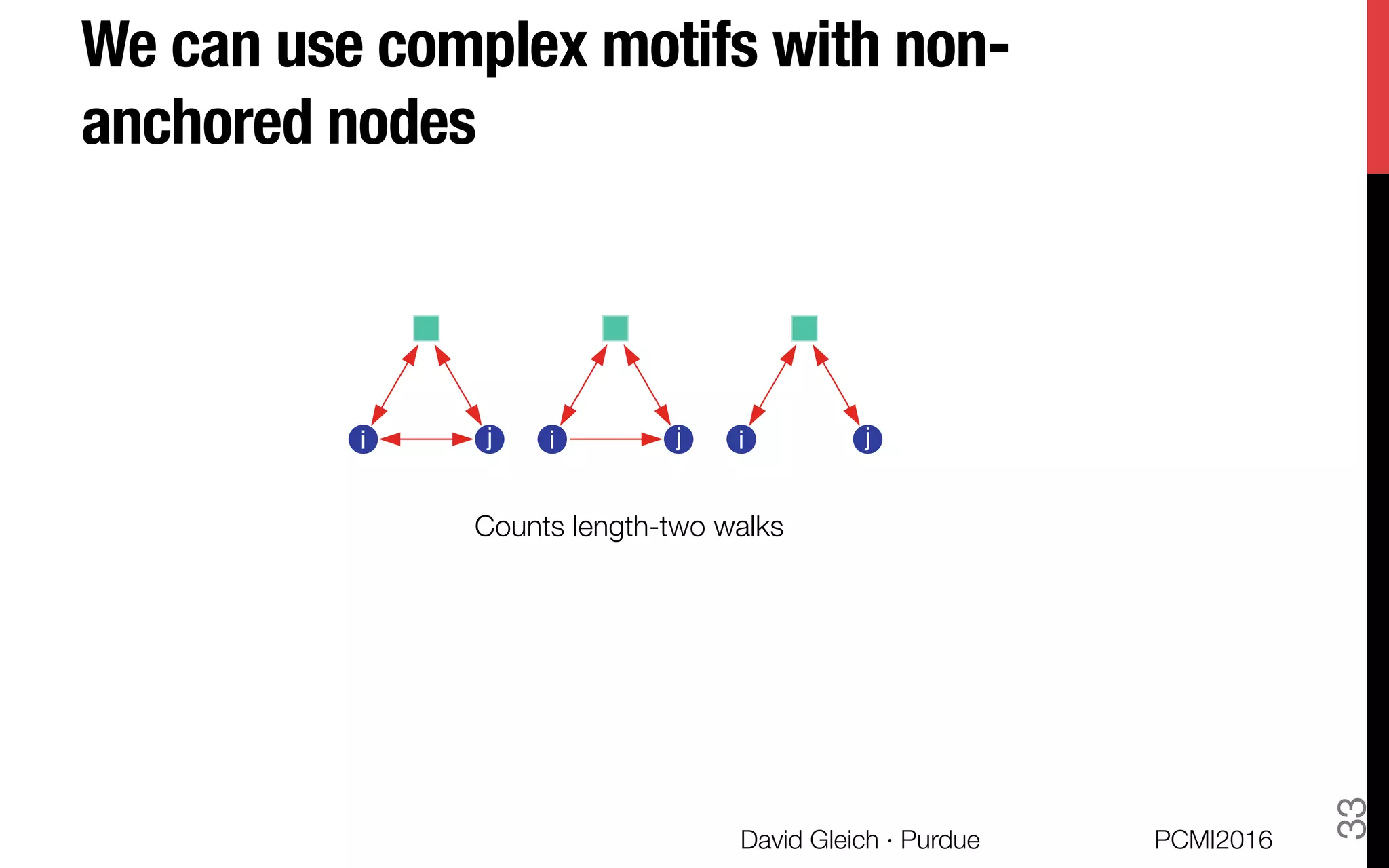
37. Related work.
§ Laplacian we propose was originally proposed by Rodríguez
[2004] and again by Zhou et al. [2006]"
Our new theory (motif Cheeger inequality) explains why these
were good ideas.
§ Falls under general strategy of encoding hypergraph partitioning
problem as graph clustering problem [Agarwal+ 06]
§ Serrour, Arenas, and Gómez, Detecting communities of triangles
in complex networks using spectral optimization, 2011.
§ Arenas et al., Motif-based communities in complex networks,
2008.
PCMI2016
David Gleich · Purdue
37

38. Paper!
Benson, Gleich, Leskovec!
Science, 2016
1. A generalized conductance metric for motifs
2. A new spectral clustering algorithm to
minimize the generalized conductance.
3. AND an associated Cheeger inequality.
4. Aquatic layers in food webs
5. Control structures in neural networks
6. Hub structure in transportation networks
7. Anomaly detection in Twitter
8. Lots of cool stuff on signed networks.
Thank you!
Joint work with "
Austin Benson and Jure
Leskovec, Stanford
Supported by NSF CAREER
CCF-1149756, IIS-1422918
IIS- DARPA SIMPLEX
9 10
8
7
2
0
4
3
11
6
5
1
PCMI2016
David Gleich · Purdue
38