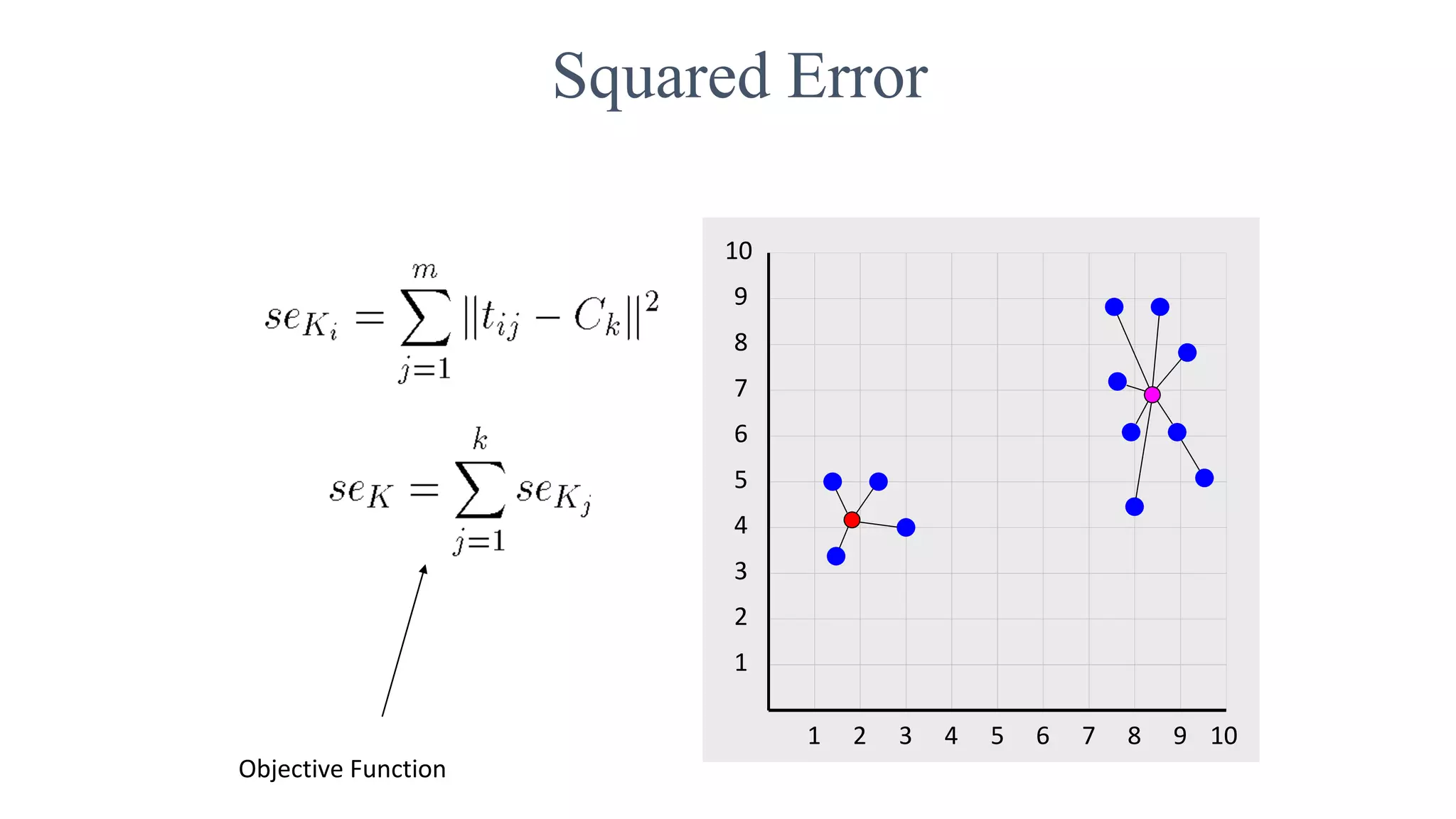
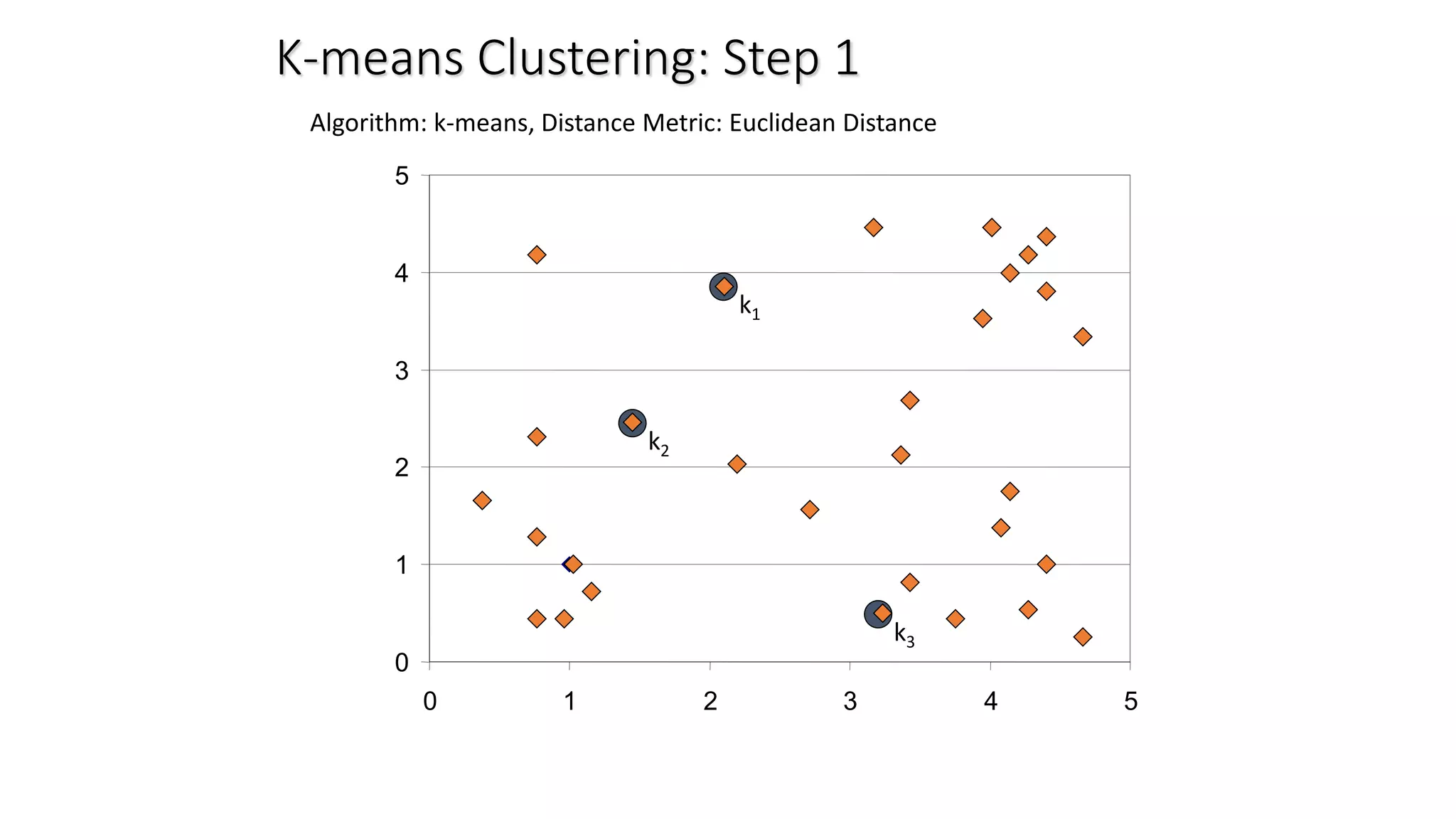
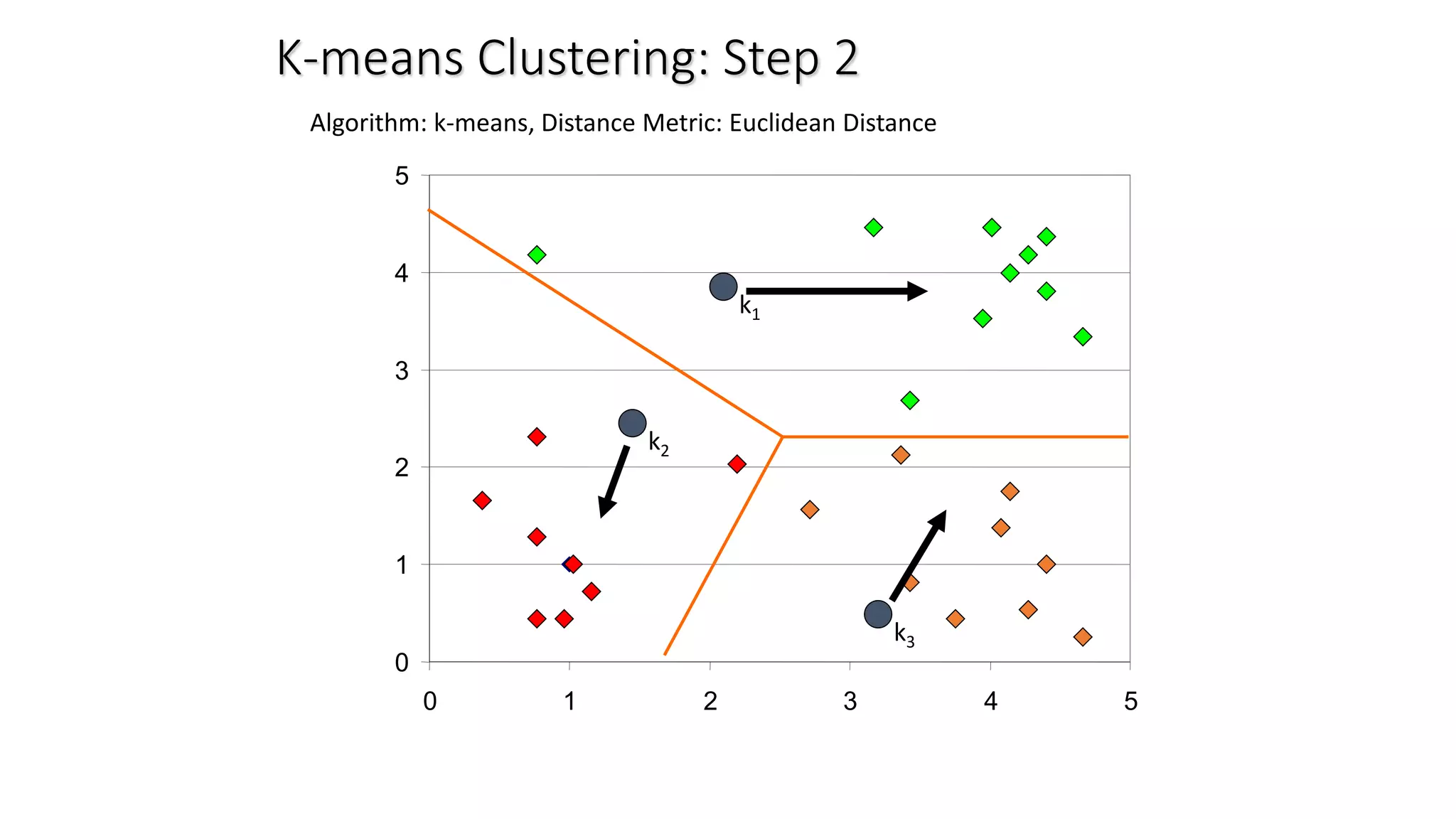
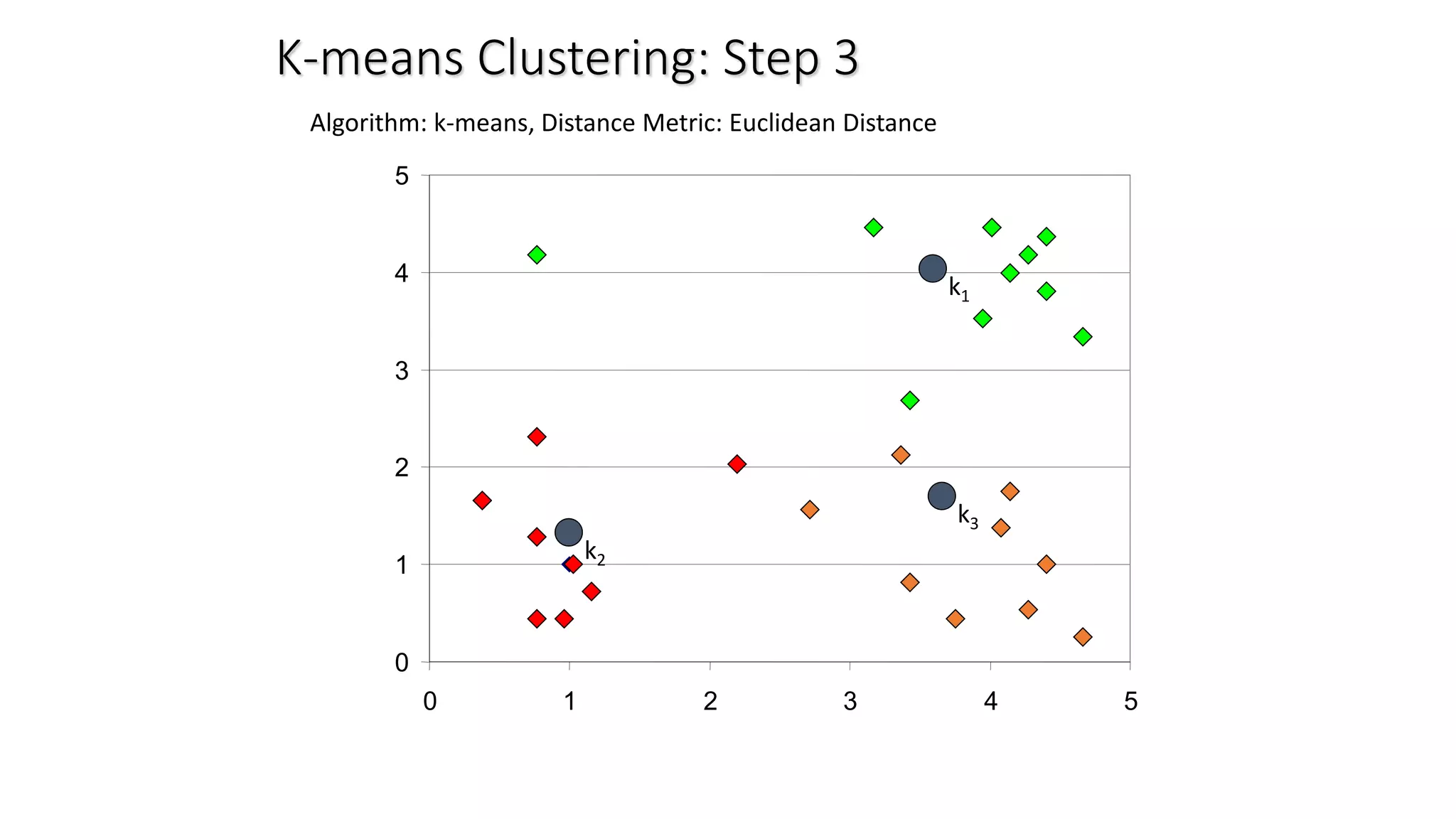
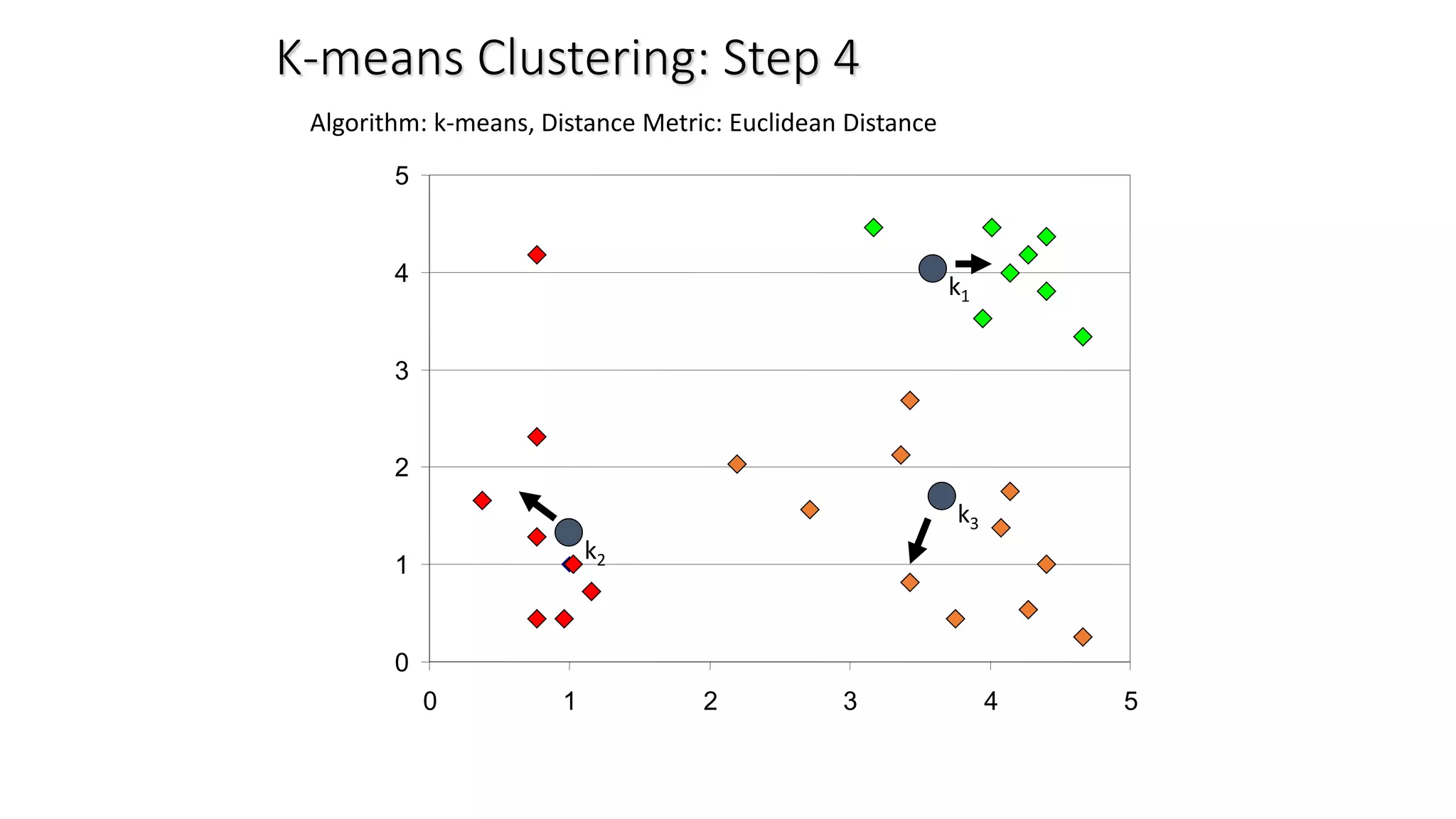
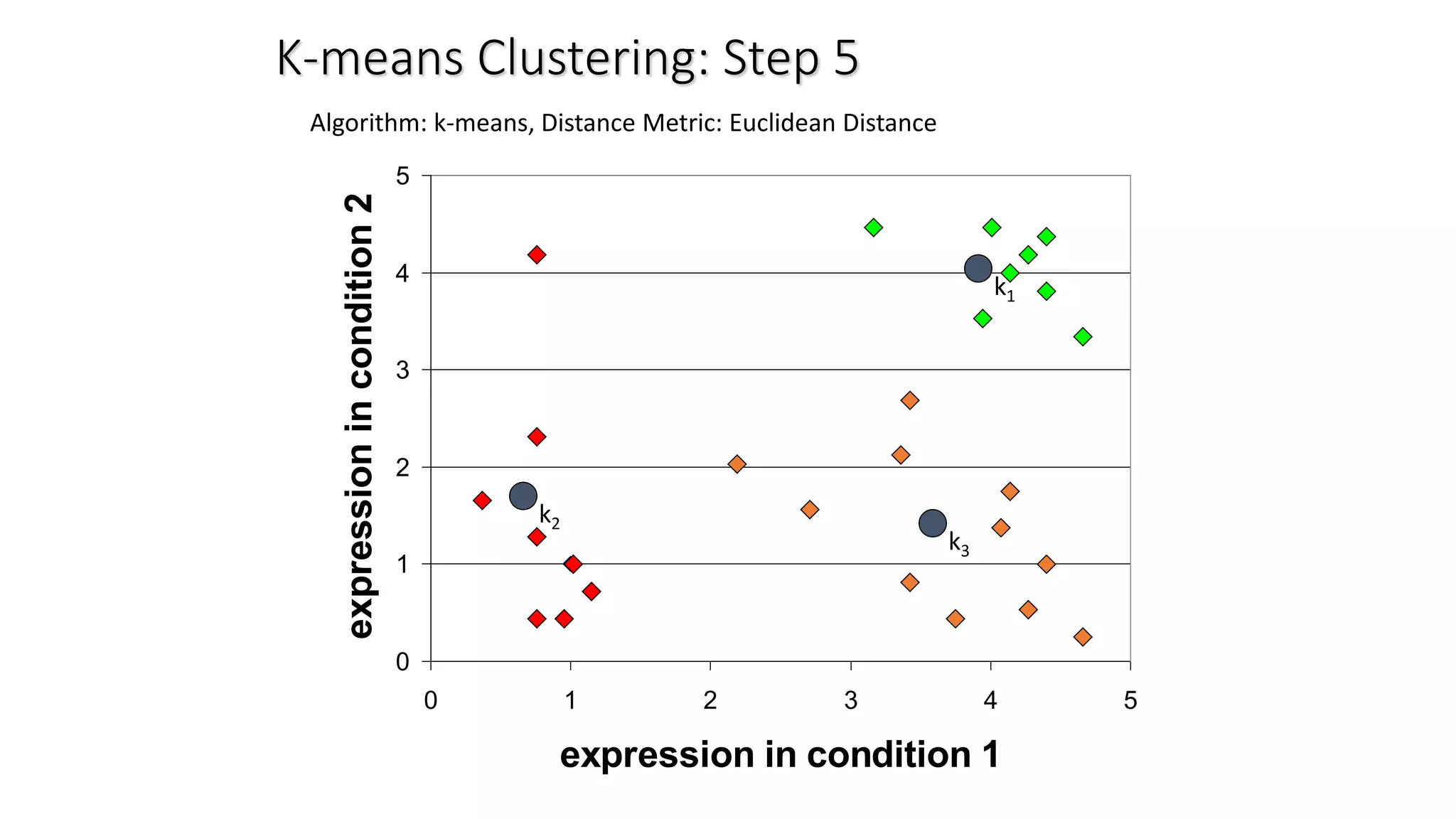
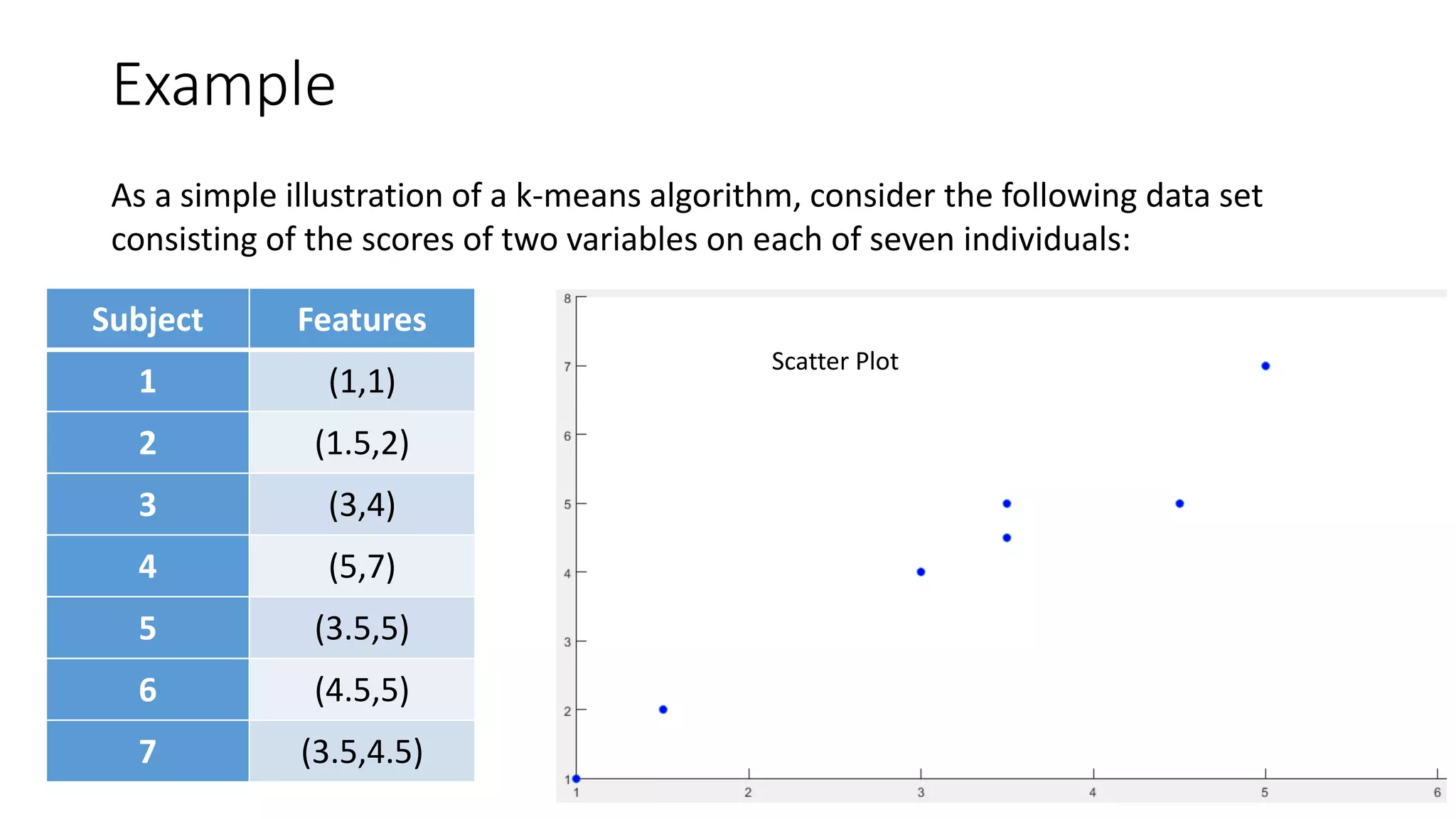
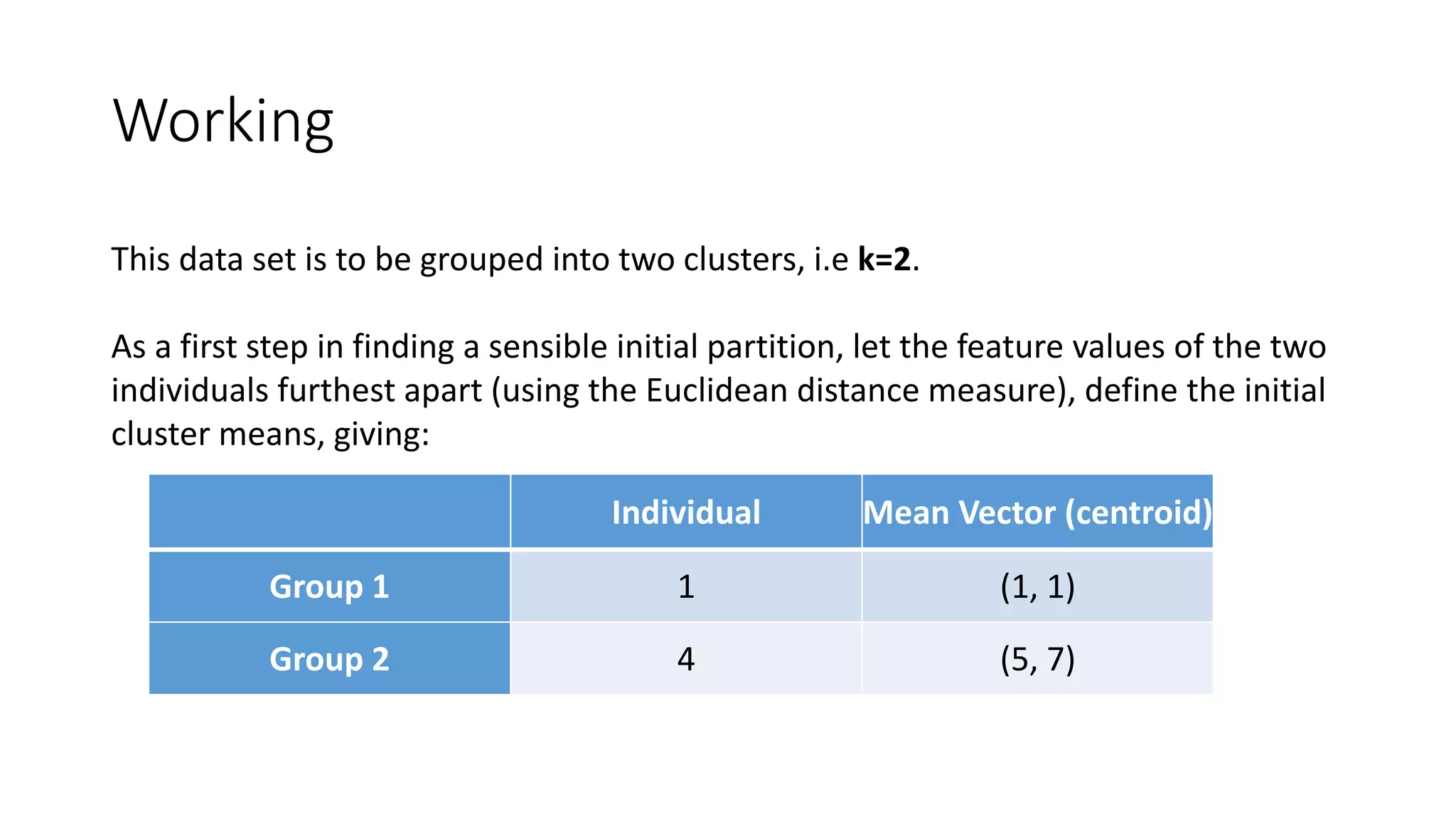
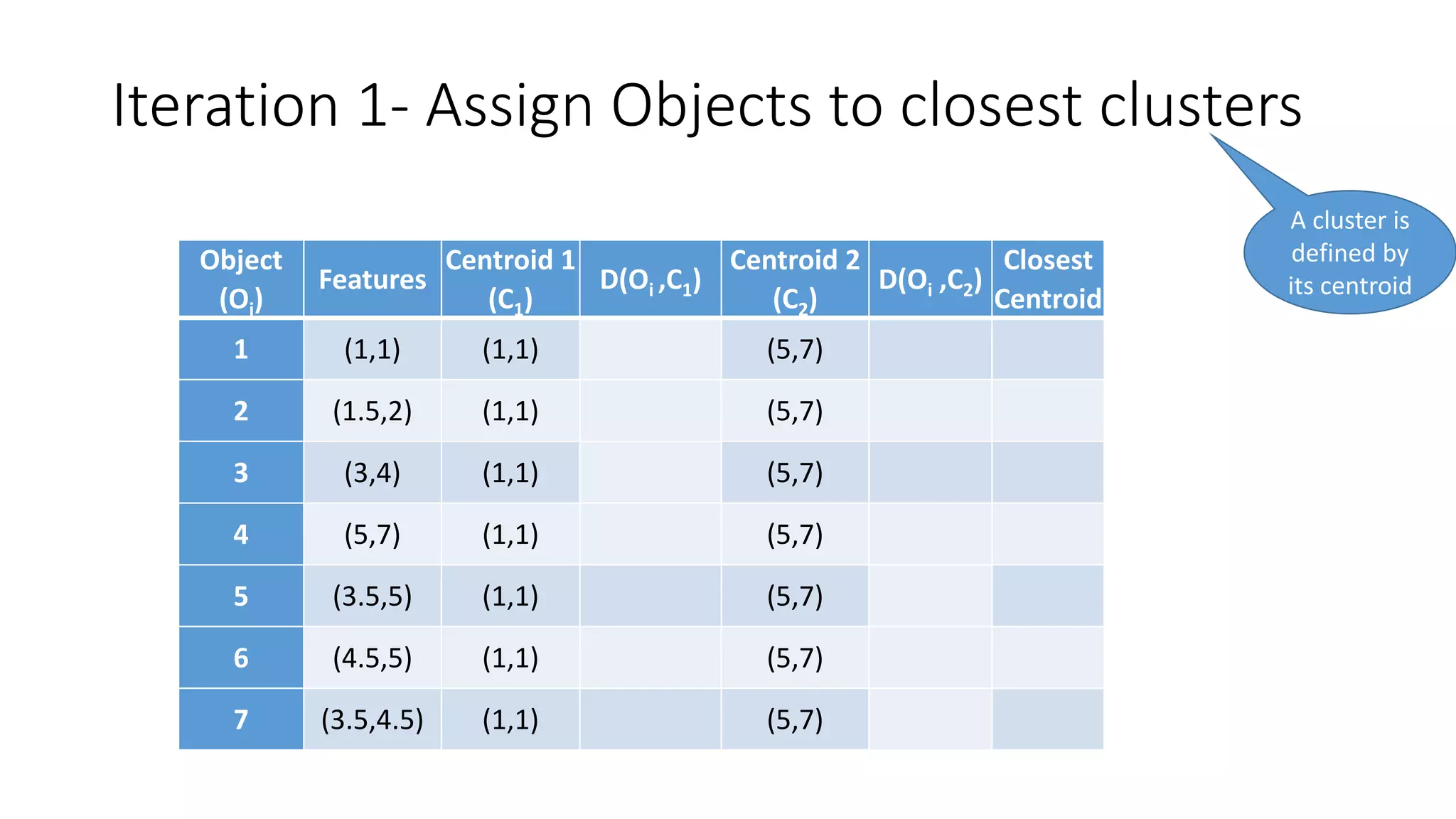
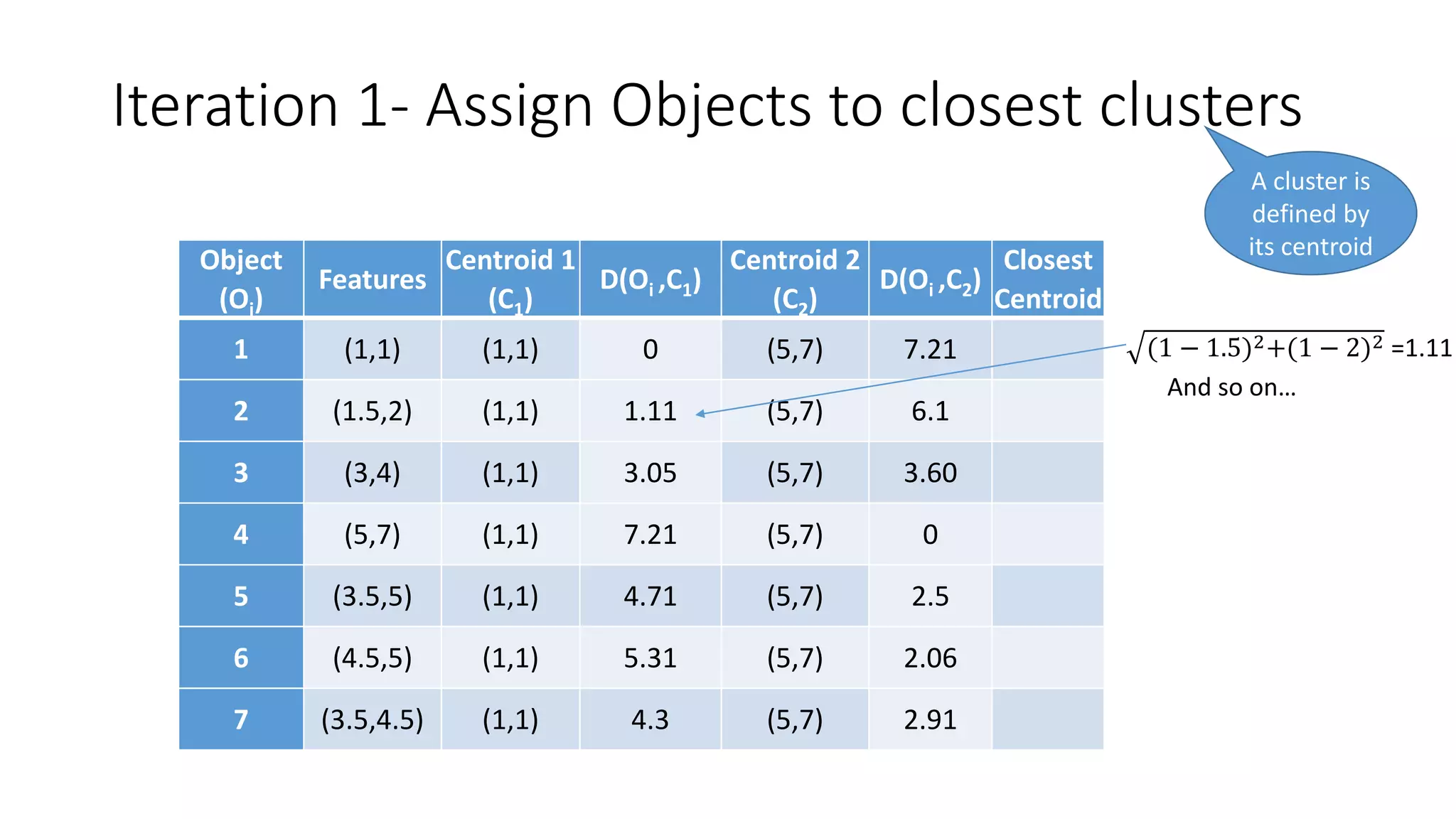
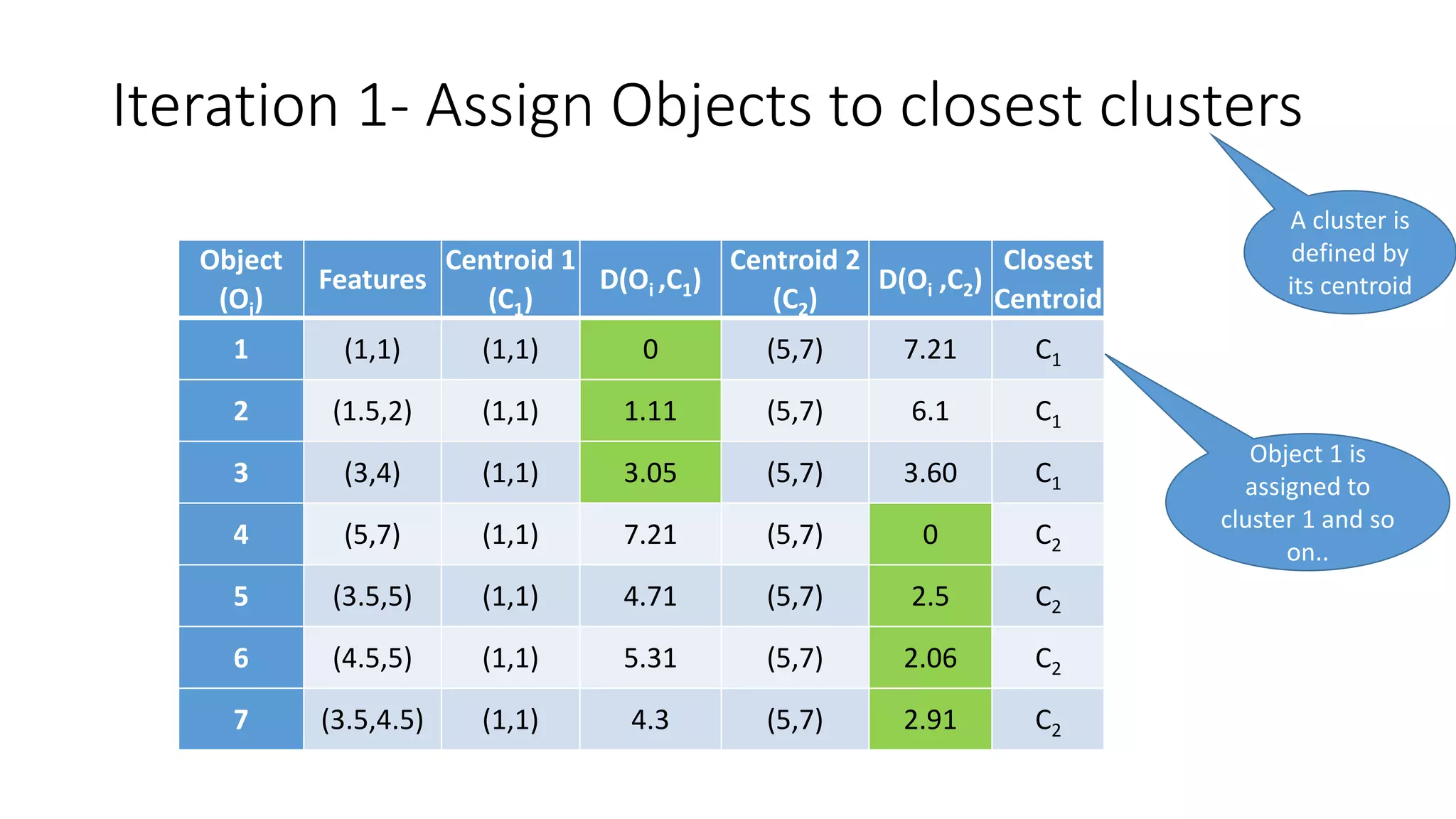
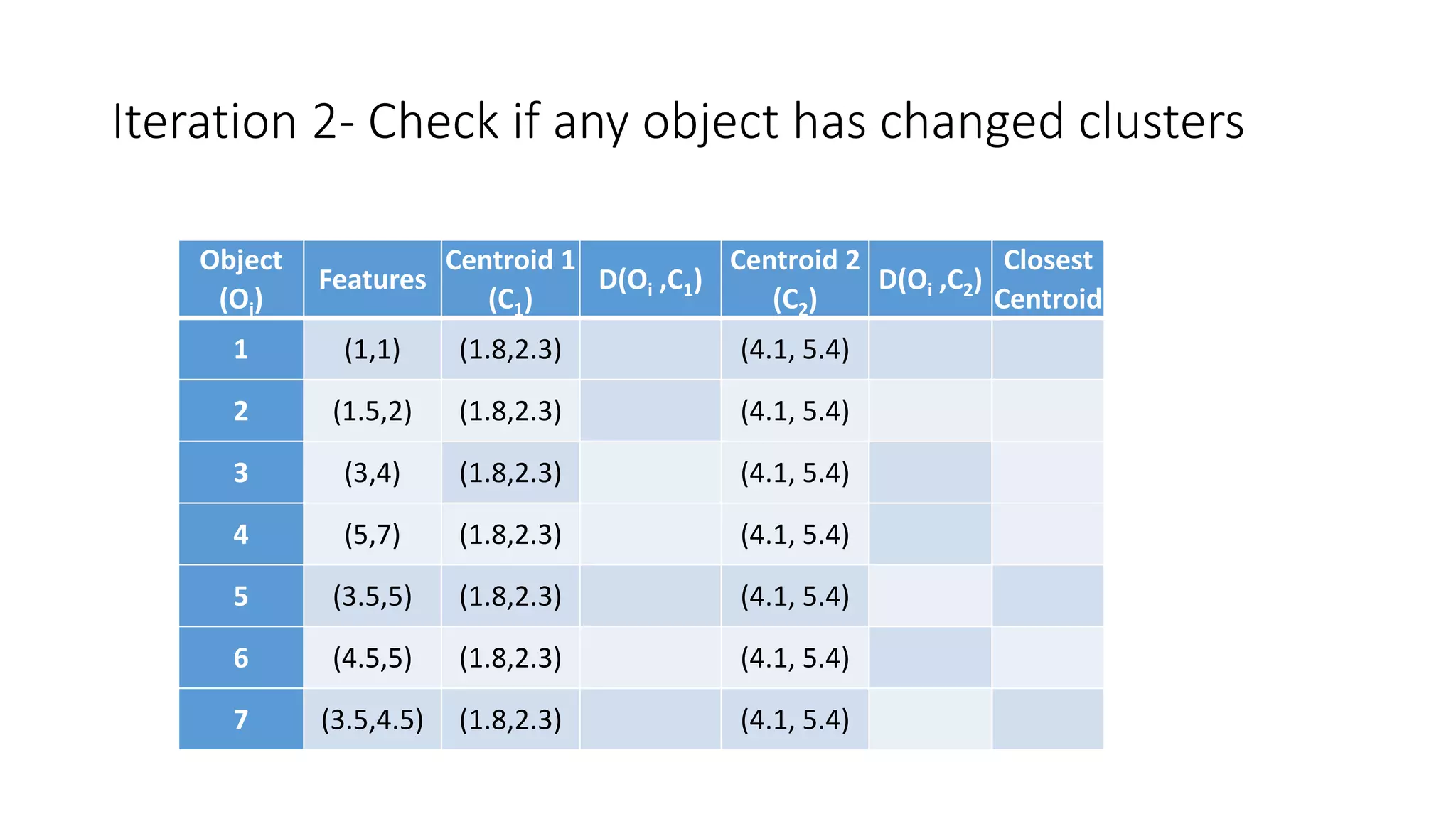
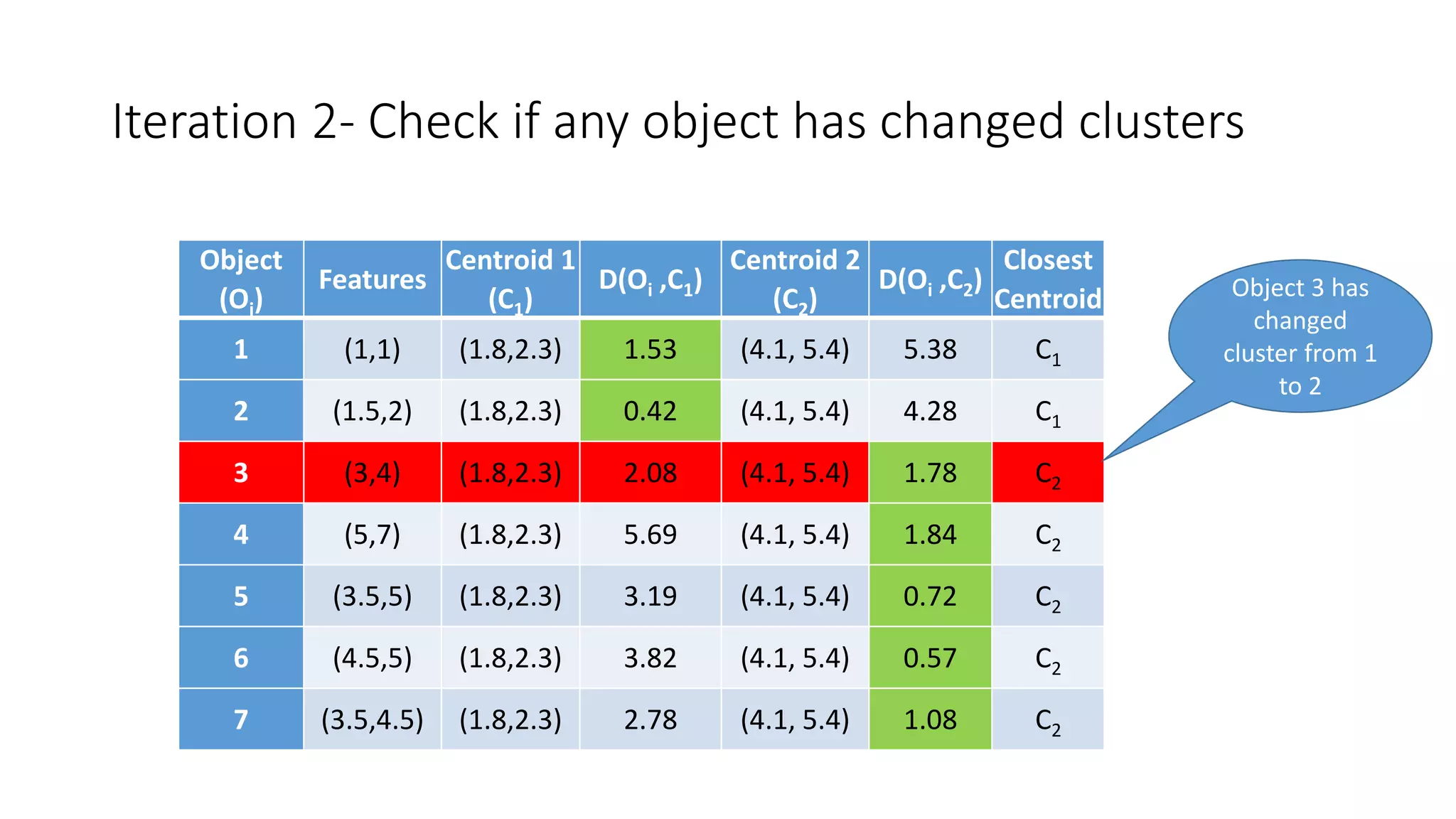
This document discusses clustering and the k-means clustering algorithm. It defines clustering as grouping a set of data objects into clusters so that objects within the same cluster are similar to each other but dissimilar to objects in other clusters. The k-means algorithm is described as an iterative process that assigns each object to one of k predefined clusters based on the object's distance from the cluster's centroid, then recalculates the centroid, repeating until cluster assignments no longer change. A worked example demonstrates how k-means partitions 7 objects into 2 clusters over 3 iterations. The k-means algorithm is noted to be efficient but requires specifying k and can be impacted by outliers, noise, and non-convex cluster shapes.

1. Clustering
Binoy B Nair

2. What is Clustering?
• Cluster: a collection of data objects
• Similar to one another within the same cluster
• Dissimilar to the objects in other clusters
• Cluster analysis
• Grouping a set of data objects into clusters
• Clustering is unsupervised classification: no predefined classes
• Typical applications
• As a stand-alone tool to get insight into data distribution
• As a preprocessing step for other algorithms

3. 3
Examples of Clustering Applications
• Marketing: Help marketers discover distinct groups in their customer bases, and then use this
knowledge to develop targeted marketing programs
• Land use: Identification of areas of similar land use in an earth observation database
• Insurance: Identifying groups of motor insurance policy holders with a high average claim cost
• Urban planning: Identifying groups of houses according to their house type, value, and
geographical location
• Seismology: Observed earth quake epicenters should be clustered along continent faults

4. 4
What Is a Good Clustering?
• A good clustering method will produce clusters with
• High intra-class similarity
• Low inter-class similarity
• Precise definition of clustering quality is difficult
• Application-dependent
• Ultimately subjective

5. 5
Requirements for Clustering in Data Mining
• Scalability
• Ability to deal with different types of attributes
• Discovery of clusters with arbitrary shape
• Minimal domain knowledge required to determine input parameters
• Ability to deal with noise and outliers
• Insensitivity to order of input records
• Robustness wrt high dimensionality
• Incorporation of user-specified constraints
• Interpretability and usability

6. 6
Major Clustering Approaches
• Partitioning: Construct various partitions and then evaluate them by some criterion
• Hierarchical: Create a hierarchical decomposition of the set of objects using some
criterion
• Model-based: Hypothesize a model for each cluster and find best fit of models to data
• Density-based: Guided by connectivity and density functions

7. 7
Partitioning Algorithms
• Partitioning method: Construct a partition of a database D of n objects into a set of k
clusters
• Given a k, find a partition of k clusters that optimizes the chosen partitioning
criterion
• Global optimal: exhaustively enumerate all partitions
• Heuristic methods: k-means and k-medoids algorithms
• k-means (MacQueen, 1967): Each cluster is represented by the center of the
cluster
• k-medoids or PAM (Partition around medoids) (Kaufman & Rousseeuw, 1987):
Each cluster is represented by one of the objects in the cluster

8. Partitional Clustering
• Each instance is placed in exactly one of K nonoverlapping
clusters.
• Since only one set of clusters is output, the user normally has
to input the desired number of clusters K.

9. 9
Similarity and Dissimilarity Between Objects
• Euclidean distance (p = 2):
• Properties of a metric d(i,j):
• d(i,j)  0
• d(i,i) = 0
• d(i,j) = d(j,i)
• d(i,j)  d(i,k) + d(k,j)
)||...|||(|),( 22
22
2
11 pp j
x
i
x
j
x
i
x
j
x
i
xjid 

10. Squared Error
10
1 2 3 4 5 6 7 8 9 10
1
2
3
4
5
6
7
8
9
Objective Function

11. Algorithm k-means
1. Decide on a value for k.
2. Initialize the k cluster centers (randomly, if necessary).
3. Decide the class memberships of the N objects by assigning them to the
nearest cluster center.
4. Re-estimate the k cluster centers, by assuming the memberships found
above are correct.
5. If none of the N objects changed membership in the last iteration, exit.
Otherwise goto 3.

12. 0
1
2
3
4
5
0 1 2 3 4 5
K-means Clustering: Step 1
Algorithm: k-means, Distance Metric: Euclidean Distance
k1
k2
k3

13. 0
1
2
3
4
5
0 1 2 3 4 5
K-means Clustering: Step 2
Algorithm: k-means, Distance Metric: Euclidean Distance
k1
k2
k3

14. 0
1
2
3
4
5
0 1 2 3 4 5
K-means Clustering: Step 3
Algorithm: k-means, Distance Metric: Euclidean Distance
k1
k2
k3

15. 0
1
2
3
4
5
0 1 2 3 4 5
K-means Clustering: Step 4
Algorithm: k-means, Distance Metric: Euclidean Distance
k1
k2
k3

16. 0
1
2
3
4
5
0 1 2 3 4 5
expression in condition 1
expressionincondition2
K-means Clustering: Step 5
Algorithm: k-means, Distance Metric: Euclidean Distance
k1
k2
k3

17. Worked out Example

18. Example
Subject Features
1 (1,1)
2 (1.5,2)
3 (3,4)
4 (5,7)
5 (3.5,5)
6 (4.5,5)
7 (3.5,4.5)
As a simple illustration of a k-means algorithm, consider the following data set
consisting of the scores of two variables on each of seven individuals:
Scatter Plot

19. Working
Individual Mean Vector (centroid)
Group 1 1 (1, 1)
Group 2 4 (5, 7)
This data set is to be grouped into two clusters, i.e k=2.
As a first step in finding a sensible initial partition, let the feature values of the two
individuals furthest apart (using the Euclidean distance measure), define the initial
cluster means, giving:

20. Working
• The remaining individuals are now examined in sequence and
allocated to the cluster to which they are closest, in terms of
Euclidean distance to the cluster mean.
• The mean vector is recalculated each time a new member is added.
• This leads to the following series of steps:

21. Iteration 1- Assign Objects to closest clusters
Object
(Oi)
Features
Centroid 1
(C1)
D(Oi ,C1)
Centroid 2
(C2)
D(Oi ,C2)
Closest
Centroid
1 (1,1) (1,1) (5,7)
2 (1.5,2) (1,1) (5,7)
3 (3,4) (1,1) (5,7)
4 (5,7) (1,1) (5,7)
5 (3.5,5) (1,1) (5,7)
6 (4.5,5) (1,1) (5,7)
7 (3.5,4.5) (1,1) (5,7)
A cluster is
defined by
its centroid

22. Iteration 1- Assign Objects to closest clusters
Object
(Oi)
Features
Centroid 1
(C1)
D(Oi ,C1)
Centroid 2
(C2)
D(Oi ,C2)
Closest
Centroid
1 (1,1) (1,1) 0 (5,7) 7.21
2 (1.5,2) (1,1) 1.11 (5,7) 6.1
3 (3,4) (1,1) 3.05 (5,7) 3.60
4 (5,7) (1,1) 7.21 (5,7) 0
5 (3.5,5) (1,1) 4.71 (5,7) 2.5
6 (4.5,5) (1,1) 5.31 (5,7) 2.06
7 (3.5,4.5) (1,1) 4.3 (5,7) 2.91
A cluster is
defined by
its centroid
(1 − 1.5)2+(1 − 2)2 =1.11
And so on…

23. Iteration 1- Assign Objects to closest clusters
Object
(Oi)
Features
Centroid 1
(C1)
D(Oi ,C1)
Centroid 2
(C2)
D(Oi ,C2)
Closest
Centroid
1 (1,1) (1,1) 0 (5,7) 7.21 C1
2 (1.5,2) (1,1) 1.11 (5,7) 6.1 C1
3 (3,4) (1,1) 3.05 (5,7) 3.60 C1
4 (5,7) (1,1) 7.21 (5,7) 0 C2
5 (3.5,5) (1,1) 4.71 (5,7) 2.5 C2
6 (4.5,5) (1,1) 5.31 (5,7) 2.06 C2
7 (3.5,4.5) (1,1) 4.3 (5,7) 2.91 C2
A cluster is
defined by
its centroid
Object 1 is
assigned to
cluster 1 and so
on..

24. Re computing Centroids at the end of Iteration 1
Individuals New Centroids
Cluster 1 1, 2, 3 C1 = ((1,1)+(1.5,2)+(3,4))/3 = (1.8, 2.3)
Cluster 2 4, 5, 6, 7 C2 =((5,7)+(3.5,5)+(4.5,5)+ (3.5,4.5))/4 = (4.1, 5.4)
Now the initial partition has changed, and the two clusters at this stage having the
following characteristics:

25. Iteration 2- Check if any object has changed clusters
Object
(Oi)
Features
Centroid 1
(C1)
D(Oi ,C1)
Centroid 2
(C2)
D(Oi ,C2)
Closest
Centroid
1 (1,1) (1.8,2.3) (4.1, 5.4)
2 (1.5,2) (1.8,2.3) (4.1, 5.4)
3 (3,4) (1.8,2.3) (4.1, 5.4)
4 (5,7) (1.8,2.3) (4.1, 5.4)
5 (3.5,5) (1.8,2.3) (4.1, 5.4)
6 (4.5,5) (1.8,2.3) (4.1, 5.4)
7 (3.5,4.5) (1.8,2.3) (4.1, 5.4)

26. Iteration 2- Check if any object has changed clusters
Object
(Oi)
Features
Centroid 1
(C1)
D(Oi ,C1)
Centroid 2
(C2)
D(Oi ,C2)
Closest
Centroid
1 (1,1) (1.8,2.3) 1.53 (4.1, 5.4) 5.38 C1
2 (1.5,2) (1.8,2.3) 0.42 (4.1, 5.4) 4.28 C1
3 (3,4) (1.8,2.3) 2.08 (4.1, 5.4) 1.78 C2
4 (5,7) (1.8,2.3) 5.69 (4.1, 5.4) 1.84 C2
5 (3.5,5) (1.8,2.3) 3.19 (4.1, 5.4) 0.72 C2
6 (4.5,5) (1.8,2.3) 3.82 (4.1, 5.4) 0.57 C2
7 (3.5,4.5) (1.8,2.3) 2.78 (4.1, 5.4) 1.08 C2
Object 3 has
changed
cluster from 1
to 2

27. Re computing Centroids at the end of Iteration 2
Individuals New Centroids
Cluster 1 1, 2 C1 = ((1,1)+(1.5,2))/2 = (1.3, 1.5)
Cluster 2 3,4, 5, 6, 7 C2 =((3,4)+(5,7)+(3.5,5)+(4.5,5)+ (3.5,4.5))/5 = (3.9, 5.1)
Now the initial partition has changed wih Object 3 getting relocated to cluster 2 and
the two clusters at this stage having the following characteristics:

28. Iteration 3- Check if any object has changed clusters
Object
(Oi)
Features
Centroid 1
(C1)
D(Oi ,C1)
Centroid 2
(C2)
D(Oi ,C2)
Closest
Centroid
1 (1,1) (1.3, 1.5) 0.58 (3.9, 5.1) 5.02 C1
2 (1.5,2) (1.3, 1.5) 0.54 (3.9, 5.1) 3.92 C1
3 (3,4) (1.3, 1.5) 3.02 (3.9, 5.1) 1.42 C2
4 (5,7) (1.3, 1.5) 6.63 (3.9, 5.1) 2.19 C2
5 (3.5,5) (1.3, 1.5) 4.13 (3.9, 5.1) 0.41 C2
6 (4.5,5) (1.3, 1.5) 4.74 (3.9, 5.1) 0.61 C2
7 (3.5,4.5) (1.3, 1.5) 3.72 (3.9, 5.1) 0.72 C2
No change in
clusters
compared to
previous
iteration

29. Conclusion
• In this example each individual is now nearer its own cluster mean
than that of the other cluster and the iteration stops, choosing the
latest partitioning as the final cluster solution.
• Hence Objects {1,2} belong to first cluster and Objects {3,4,5,6,7}
belong to second cluster.

30. Notes
• The iterative relocation would continue until no more relocations occur.
• Luckily, in the example, we got the no-relocation condition satisfied in 3
iterations, but this is not usually the case. It might require hundreds of
iterations depending on the dataset.
• Also, it is possible that the k-means algorithm won't find a final solution at
all.
• In this case it would be a good idea to consider stopping the algorithm
after a pre-chosen maximum of iterations.

31. Comments on the K-Means Method
• Strength
• Relatively efficient: O(tkn), where n is # objects, k is # clusters, and t is # iterations.
Normally, k, t << n.
• Often terminates at a local optimum. The global optimum may be found using
techniques such as: deterministic annealing and genetic algorithms
• Weakness
• Applicable only when mean is defined, then what about categorical data?
• Need to specify k, the number of clusters, in advance
• Unable to handle noisy data and outliers
• Not suitable to discover clusters with non-convex shapes

32. 32
Summary
• K-means algorithm is a simple yet popular method for clustering analysis
• Its performance is determined by initialisation and appropriate distance
measure
• There are several variants of K-means to overcome its weaknesses
• K-Medoids: resistance to noise and/or outliers
• K-Modes: extension to categorical data clustering analysis
• CLARA: extension to deal with large data sets
• Mixture models (EM algorithm): handling uncertainty of clusters
Online tutorial: the K-means function in Matlab
https://www.youtube.com/watch?v=aYzjenNNOcc

33. References
• http://mnemstudio.org/clustering-k-means-example-1.htm
• Ke Chen, K-means Clustering ,COMP24111-Machine Learning,
University of Manchester, 2016.
• {Insert Reference}/ 10.ppt
• {Insert Reference}/MachinLearning3.ppt