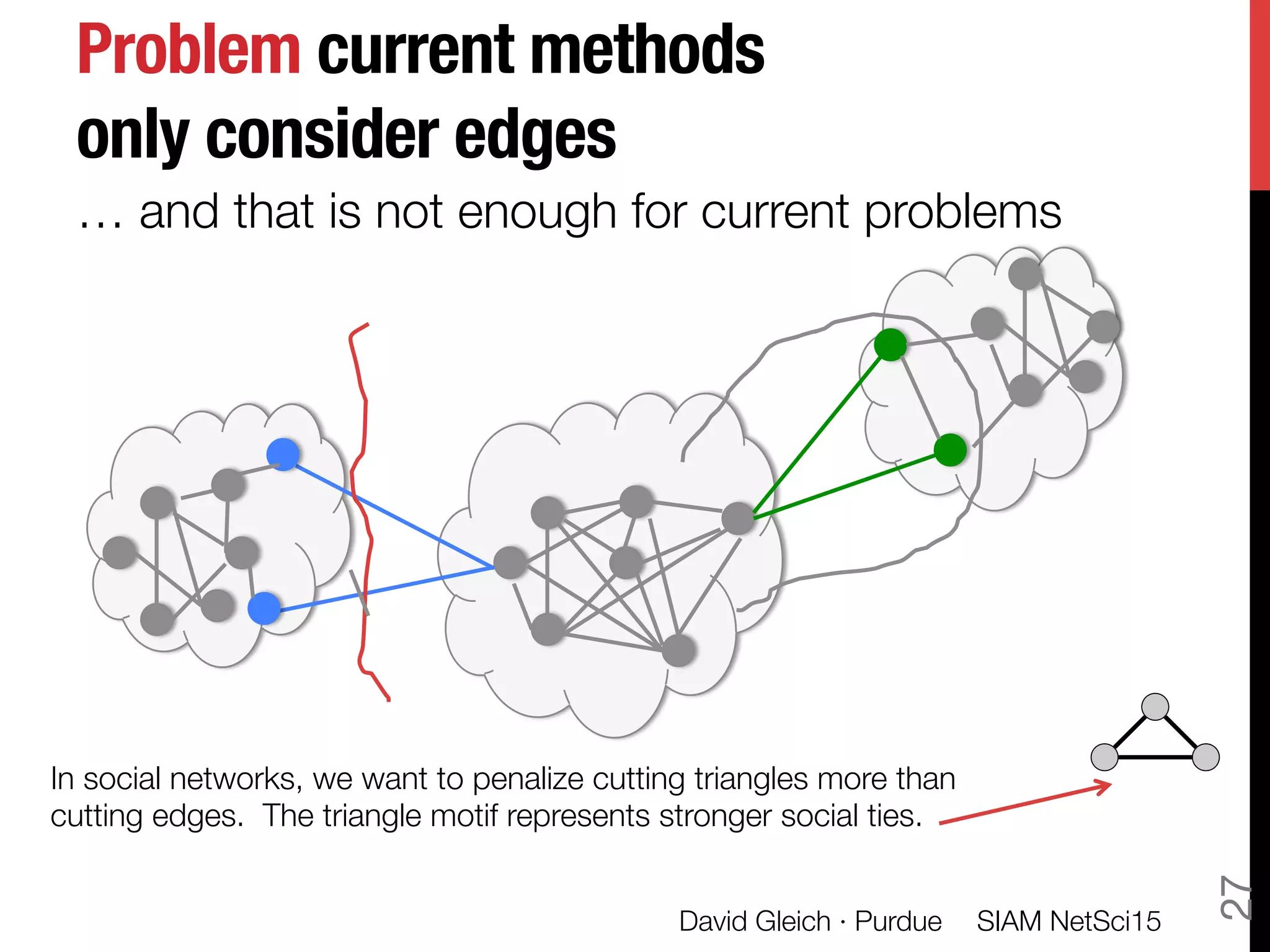
The document discusses the concept of spacey random walks on higher-order Markov chains, exploring their utility in approximating stationary distributions and their connection to PageRank algorithms. It introduces the notion of vertex-reinforced random walks, detailing how they operate and their relevance in analyzing complex data structures. The talk also touches upon spectral clustering of tensors and highlights possible applications in social networks and transcription networks.

1. Spacey Random Walks on
Higher-Order Markov Chains
David F. Gleich!
Purdue University!
Joint work with
Austin Benson,
Lek-Heng Lim,
supported by "
NSF CAREER
CCF-1149756
IIS-1422918
SIAM NetSci15
David Gleich · Purdue
1

2. 2
Spacey walk !
on Google Images
From Film.com

3. WARNING!!
This talk presents the “forward” explicit
derivation (i.e. lots of little steps)
rather than the implicit “backwards”
derivation (i.e. big intuitive leaps)
SIAM NetSci15
David Gleich · Purdue
3

4. PageRank:The initial condition
My dissertation"
Models & Algorithms for PageRank Sensitivity
The essence of PageRank!
Take any Markov chain P, PageRank "
creates a related chain with great “utility”
• Unique stationary distribution
• Fast convergence
• Modeling flexibility
(I ↵P)x = (1 ↵)v
PageRank
beyond
the Web
arXiv:1407.5107
by Jessica Leber
Fast Magazine
SIAM NetSci15
David Gleich · Purdue
4

5. Be careful about what you
discuss after a talk…
I gave a talk!
at the Univ. of Chicago and visited Lek-heng Lim!
He told me about a new idea!
in Markov chains analysis and tensor eigenvalues
SIAM NetSci15
David Gleich · Purdue
5

6. Approximate stationary distributions
of higher-order Markov chains
A higher order Markov chain!
depends on the last few states.
These become Markov chains on the product state space."
But that’s usually too large for stationary distributions.
The approximation!
is that we form a rank-1 approximation of that stationary
distribution object.
Due to Michael Ng and collaborators
P(Xt+1 = i | history) = P(Xt+1 = i | Xt = j, Xt 1 = k)
P(X = [i, j]) = xi xj
SIAM NetSci15
David Gleich · Purdue
6
P(X = [i, j]) = Xi,j

7. Why?
SIAM NetSci15
David Gleich · Purdue
7
Multidimensional, multi-
ceted data from inform-
ics and simulations
a
b
m
li
This propos
dimensiona
We want to analyze
higher-order relationships
and multi-way data and …
Things like
• Enron emails
• Regular hypergraphs
And there’s three+ indices!
So it’s a "
higher-order Markov chain

8. Approximate stationary distributions
of higher-order Markov chains
The new problem!
of computing an approx. stationary dist. is a tensor eigenvector
The new problem’!
• existence is guaranteed under mild conditions
• uniqueness …
• convergence …
Due to Michael Ng and collaborators
xi =
X
jk
Pijk xj xk or x = Px2
require heroic algebra
(and are hard to check)
SIAM NetSci15
David Gleich · Purdue
8

9. Some small quick notes
A stochastic matrix M is a Markov chain
A stochastic hypermatrix / tensor / probability P table "
is a higher-order Markov chain
SIAM NetSci15
David Gleich · Purdue
9
Multidimensional, multi-
faceted data from inform-
atics and simulations
a
b
m
li
This propos
dimensiona

10. PageRank to the rescue!
What if we looked at these approx. stat.
distributions of a PageRank modified higher-
order chain?
Multilinear PageRank!
• Formally the Li & Ng approx. stat. dist. of the
PageRank modified higher order Markov chain
• Guaranteed existence!
• Fast convergence ?
• Uniqueness ?
x = ↵Px2
+ (1 ↵)v
Multilinear PageRank"
Gleich, Lim, Yu"
arXiv:1409.1465
when alpha < 1/order !
when alpha < 1/order !
SIAM NetSci15
David Gleich · Purdue
10

11. One nagging question …!
Is there a stochastic process that
underlies this approximation?
SIAM NetSci15
David Gleich · Purdue
11

12. Meanwhile … "
Spectral clustering of tensors
Austin Benson (a colleague) asked"
if there were any interesting method to “cluster” tensors.
“Recall” spectral clustering on graphs!
!
SIAM Data Mining 2015, arXiv:1502.05058
graph ! random walk
! second eigenvector
! sweep cut partition
SIAM NetSci15
David Gleich · Purdue
12
MT
y = 2y
¯SS
min
S
(S) = min
S
#(edges cut)
min(vol(S), vol( ¯S))

13. Meanwhile … "
Spectral clustering of tensors
Austin Benson (a colleague) asked"
if there were any interesting method to “cluster” tensors.
“Conjecture” spectral clustering on tensors!
!
SIAM Data Mining 2015, arXiv:1502.05058
graph/tensor ! higher-order random walk
! second eigenvector
! sweep cut partition
??????!
SIAM NetSci15
David Gleich · Purdue
13

14. We tried many
• apriori good and
• retrospectively bad
ideas for the second eigenvector
SIAM NetSci15
David Gleich · Purdue
14

15. Austin and I were talking one day …
... about the problem of the process. (He was using Multilinear
PageRank as the “first” eigenvector.) He observed that
One of the five algorithms !
for multilinear PageRank uses a seq. of Markov chains.
Is there some way to turn this into a random walk?
xk+1 = stat. dist. of Markov chain based on ↵, v, P, and xk
SIAM NetSci15
David Gleich · Purdue
15

16. EUREKA!
SIAM NetSci15
David Gleich · Purdue
16

17. The spacey random walk
Consider a higher-order Markov chain.
If we were perfect, we’d figure out the stationary
distribution of that. But we are spacey!
• On arriving at state j, we promptly "
“space out” and forget we came from k.
• But we still believe we are “higher-order”
• So we invent a state k by drawing a random
state from our history.
P(Xt+1 = i | history) = P(Xt+1 = i | Xt = j, Xt 1 = k)
SIAM NetSci15
David Gleich · Purdue
17

18. The spacey random walk
This is a vertex-reinforced random walk! "
e.g. Polya’s urn.
Pemantle, 1992; Benaïm, 1997; Pemantle 2007
SIAM NetSci15
David Gleich · Purdue
18
P(Xt+1 = i | Xt = j and the right filtration on history)
=
X
k
Pi,j,k Ck (t)/(t + n)
Let Ct (k) = (1 +
Pt
s=1 Ind{Xs = k})
How often we’ve visited
state k in the past

19. Stationary distributions of vertex
reinforced random walks
A vertex-reinforced random walk at time t transitions
according to a Markov matrix M given the observed
frequencies.
This has a stationary distribution, iff the dynamical system
converges.
SIAM NetSci15
David Gleich · Purdue
19
dx
dt
= ⇡[M(x)] x
P(Xt+1 = i | Xt = j and the right filtration on history)
= [M(t)]i,j
= [M(c(t))]i,j
⇡[M] is a map to the stat. dist.
M. Benïam 1997

20. The Markov matrix for "
Spacey Random Walks
A necessary condition for a stationary distribution
(otherwise makes no sense)
SIAM NetSci15
David Gleich · Purdue
20
Property B. Let P be an order-m, n dimensional probability table. Then P has
property B if there is a unique stationary distribution associated with all stochastic
combinations of the last m 2 modes. That is, M =
P
k,`,... P(:, :, k, `, ...) k,`,... defines
a Markov chain with a unique Perron root when all s are positive and sum to one.
dx
dt
= ⇡[M(x)] x
M =
X
k
P(:, :, k)xk
This is the transition probability associated
with guessing the last state based on history!

21. We have all sorts of cool results on spacey
random walks… e.g.
Suppose you have a Polya Urn with memory… "
Then it always has a stationary distribution!
SIAM NetSci15
David Gleich · Purdue
21

22. Back to Multilinear PageRank
The Multilinear PageRank problem is what we call a
spacey random surfer model.
• This is a spacey random walk
• We add random jumps with probability (1-alpha)
It’s also a vertex-reinforced random walk.
Thus, it has a stationary probability if
converges.
SIAM NetSci15
David Gleich · Purdue
22
dx
dt
= ⇡[M(x)] x
M(x) = ↵
P
k P(:, :, k)xk
+ (1 ↵)v
Which occurs when alpha < 1/order !

23. Some interesting notes about vertex
reinforced random walks
• The power method is NOT the natural
algorithm! It’s to evolve the ODE.
• It’s unclear if there are any structural
properties that guarantee a stationary
distribution (except for something like the
Multilinear PageRank equation)
• Can be tough to analyze the resulting ODEs
• Asymptotically creates a Markov chain!
SIAM NetSci15
David Gleich · Purdue
23

24. … back to spectral clustering …
SIAM NetSci15
David Gleich · Purdue
24

25. Meanwhile … "
Spectral clustering of tensors
Austin Benson (a colleague) asked"
if there were any interesting method to “cluster” tensors.
“Conjecture” spectral clustering on tensors!
!
SIAM Data Mining 2015, arXiv:1502.05058
graph/tensor ! higher-order random walk
! second eigenvector
! sweep cut partition
??????!
SIAM NetSci15
David Gleich · Purdue
25

26. Meanwhile … "
Spectral clustering of tensors
Austin Benson (a colleague) asked"
if there were any interesting method to “cluster” tensors.
“Conjecture” spectral clustering on tensors!
!
SIAM Data Mining 2015, arXiv:1502.05058
graph/tensor ! higher-order random walk
! second eigenvector
! sweep cut partition
SIAM NetSci15
David Gleich · Purdue
26
M(x)T
y = 2y
Use the asymptotic
Markov matrix!

27. Problem current methods
only consider edges
… and that is not enough for current problems
SIAM NetSci15
David Gleich · Purdue
27
In social networks, we want to penalize cutting triangles more than
cutting edges. The triangle motif represents stronger social ties.

28. Problem current methods
only consider edges
SIAM NetSci15
David Gleich · Purdue
28
SPT16
HO
CLN1
CLN2
SWI4_SWI6
In transcription networks, the ``feedforward loop” motif represents
biological function. Thus, we want to look for clusters of this structure.

29. An example with a layered flow network
SIAM NetSci15
David Gleich · Purdue
29
0
12
3
4 5
6 7
8 9
10 11
§ The network “flows” downward
§ Use directed 3-cycles to model flow
i
kj
i
kj
i
kj
i
kj
1 1 1 2
§ Tensor spectral clustering: {0,1,2,3}, {4,5,6,7}, {8,9,10,11}
§ Standard spectral: {0,1,2,3,4,5,6,7}, {8,10,11}, {9}

30. SIAM NetSci15
David Gleich · Purdue
30
WAW2015
EURANDOM
–
Eindhoven
–
Netherlands
Workshop on Algorithms and Models for the Web Graph
(but it’s grown to be all types of network analysis)
December 10-­‐11
Winter School on Complex Network and Graph Models
December 7-­‐8
Submissions Due July 25th!

31. Time for Lots of Questions!
Manuscripts!
Li, Ng. On the limiting probability distribution of a transition
probability tensor. Linear & Multilinear Algebra 2013.
Gleich. PageRank beyond the Web. (accepted at SIAM Review)
Gleich, Lim, Yu. Multilinear PageRank. (under review…)
Benson, Gleich, Leskovec. Tensor Spectral Clustering for
partitioning higher order network structures. SDM 2015, arXiv:"
https://github.com/arbenson/tensor-sc
Benson, Gleich, Leskovec. Forthcoming. (Much better method…)
Benson, Gleich, Lim. The Spacey Random Walk. In prep.
SIAM NetSci15
David Gleich · Purdue
31