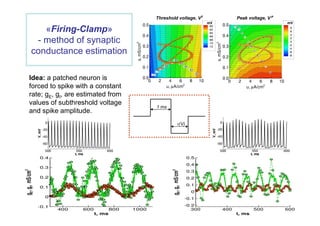
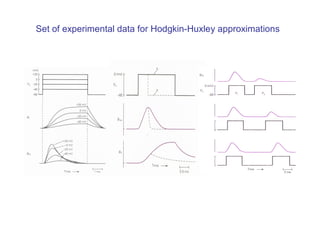
The document discusses neuron-computer interfaces utilizing dynamic-clamp experiments with leaky integrate-and-fire and Hodgkin-Huxley neuron models. It elaborates on the control parameters for neuron dynamic-clamp, the modeling of synaptic and voltage-gated currents, and the implications for neuronal excitability and firing characteristics. The study emphasizes the importance of dynamic clamp for measuring neuronal firing dynamics and estimating synaptic conductances in vivo.

1. Neuron-computer interface
in Dynamic-Clamp experiments
Anton V. Chizhov
A.F.Ioffe Physico-Technical Institute of
Russian Academy Sciences,
St.-Petersburg, Russia

2. Leaky integrate-and-fire model
Hodgkin-Huxley neuron model
Control parameters of neuron
Dynamic-clamp
• Artificial synaptic current
• Artificial voltage-dependent
current
• Synaptic conductance
estimation

3. Leaky Integrate-and-Fire neuron
dV
C   g L (V ( t )  V L )  i S V is the membrane potential; I is the input (synaptic) current,
dt C is the membrane capacity; gL is the membrane
conductance; Vrest is the rest potential; VT is the threshold
If V  VT then V  Vreset potential; Vreset is the reset potential.
C
m 
gL

4. Firing rate dependence on current (F-I-curve)
gL

 V  i / g V 
C ln L S L T
 V  i / g V 

 L S L reset 

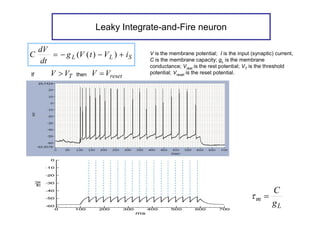
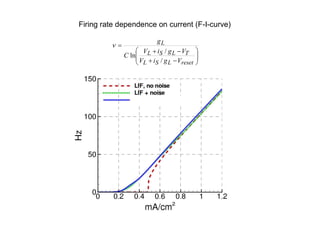
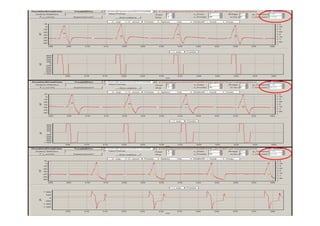
5. V(x)
r Внутри V(x+Δx)
jm
C
im
 g S (V  VL )  iS
φ≈0
Снаружи
h
VNa V
gNa
gK
Vrest
VK
[Покровский, 1978]

6. Set of experimental data for Hodgkin-Huxley approximations

7. Model of a pyramidal neuron
dV
C   I Na  I DR  I A  I M  I H  I L  I AHP  iS
dt
p q
E X P Е R I М Е N Т
I ...  g... x (t ) y (t ) (V (t )  V... )
dx x (U )  x
 ,
dt  x (U )
dy y (U )  y

dt  y (U )
Approximations for I Na , I DR , I A , I M , I H
are taken from [L.Graham, 1999]; IAHP is
from [N.Kopell et al., 2000]
Model with noise
Color noise model for
synaptic current IS is the
Ornstein-Uhlenbeck process:
diS 0
  iS (t )  iS  2  (t )
dt

8. E X P E R I M E N T
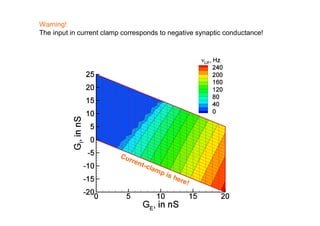
Control parameters of
a neuron
dV ( t )
C   g Na m 3 (V , t )h (V , t )(V (t )  VNa ) 
dt
4  2V
 g K n (V , t )(V (t )  VK )  g L (V ( t )  VL )  iS  k 2
x
Voltage-gated channels kinetics:
dm m (V )  m
 
MODEL
dt  m (V )
dh h (V )  h [Hodgkin, Huxley, 1952]
 
dt  h (V )
dn n (V )  n
 
dt  n (V )
Property: Neuron is controlled by two parameters
[Покровский, 1978]
iS  GE (V  VE )  GI (V  VI )  I electrode   s (V  V0 )  u
u  GE (VE  V0 )  GI (VI  V0 )  I electrode
s  GE  GI

9. The case of many voltage-independent synapses
dV
C   I ionic channels (V , t )   g S (t ) (V (t )  VS )  I el (t )
dt S
s(t )   g S (t )
S
u (t )   g S (t ) (VS  V0 )  I el (t )
S
,
dV
C   I ionic channels (V , t )  s(t ) (V (t )  V0 )  u(t ),
dt

10. Warning!
The input in current clamp corresponds to negative synaptic conductance!
Cur
rent
-c lam
p is
her
e !

11. Whole-cell patch-clamp:
Current- and Voltage-Clamp modes
“Current clamp”, “Voltage clamp”,
V(t) is registered I(t) is registered
const

12. Whole-cell patch-clamp:
Dynamic-Clamp mode
Conductance clamp (Dynamic clamp):
V(t) is registered,
I(V,t) = gDC (V,t) (V(t)-VDC) is injected
• For artificial passive leaky channel gDC=const
• For artificial synaptic channel gDC(t) reflects the synaptic kinetics
• For voltage-gated channel gDC(V(t),t) is described by ODEs

13. Conductance clamp (Dynamic clamp):
“Current clamp” I(V(t))=gDC (V(t)-VDC) is injected

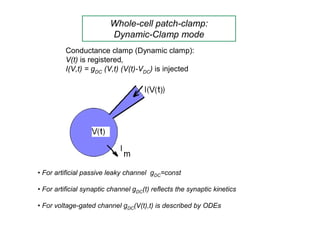
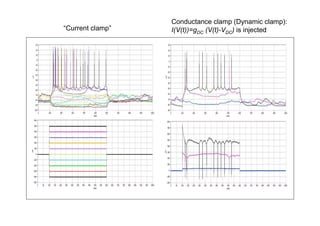
14. Dynamic clamp for synaptic current
[Sharp AA, O'Neil MB, Abbott LF, Marder E. Dynamic clamp: computer-generated
conductances in real neurons. // J.Neurophysiol. 1993, 69(3):992-5]
I  g GABA (t ) (V  VGABA )
 
gGABA (t )  gGABA e  t /  1  e  t /  2 ,  1  5 s,  2  15 s, gGABA  8 nS
max max

15. Control
Dynamic clamp
for spontaneous
potassium
channels
I  g (t )(V  VK )
d 2g dg
 1 2 2  ( 1   2 )  g 
artificial K-channels dt dt
 g max  2 1   (t  ti )
i
 1  5ms,  2  200ms
VK  70mV
g max  1nS

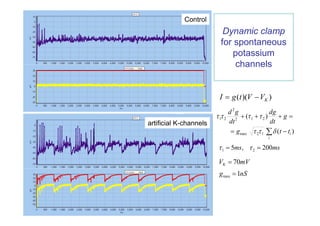
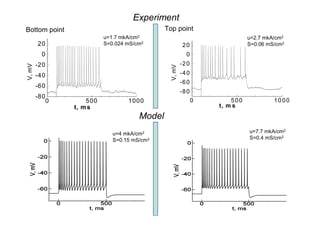
16. Dynamic clamp Model [Graham, 1999] for
to study firing properties of CA1 pyramidal neuron
neuron
Hz
0.6 80
Experiment: pyramidal cell 60
of visual cortex 0.5 40
Hz
0.06 Hz 20
0.4
s, mS/cm2
(2.7; 0.06)
110
0.05 100
0
90
0.04 80 0.3
s, mS/cm2
70
60
0.03 50
40 0.2
(1.7; 0.024) 30
0.02 20
0.01
10
0 0.1
0 1 2 3 0 2 4 6 8 10
2 2
u, A/cm u,mkA/cm

17. Experiment
Bottom point Top point
u=1.7 mkA/cm2 u=2.7 mkA/cm2
20 S=0.024 mS/cm2 20 S=0.06 mS/cm2
0 0
-20 -2 0
V, mV
V, mV
-40 -4 0
-6 0
-60
-8 0
-80
0 500 1000 0 500 1000
t, m s t, m s
Model
u=4 mkA/cm2 u=7.7 mkA/cm2
S=0.15 mS/cm2 S=0.4 mS/cm2

18. Divisive effect of shunting inhibition is due to spike threshold
sensitivity to slow inactivation of sodium channels
dV T V0T  V T
  V T   (t  t i
spike
)
dt  i

19.  2 Rate
Gex Ginh
Total Response (all spikes during 500ms-step)
Only 1st spikes Only 1st interspike intervals

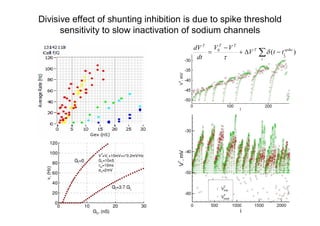
20. Dynamic clamp for voltage-gated current:
compensation of INaP
Hippocampal Pyramidal Neuron In Vitro
[Vervaeke K, Hu H., Graham L.J., Storm J.F.
Contrasting effects of the persistent Na+
current on neuronal excitability and spike
timing, Neuron, v49, 2006]

21. Medium
electric Dynamic clamp
conductance for electric
couplings
between real and
modeled neurons
I  g (V exp  V mod )
g  const
High
electric
conductance

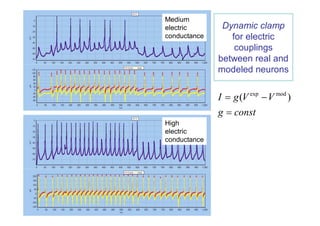
22. Dynamic clamp for synaptic conductance
estimations in-vivo
Preferred direction Null direction
V
Эксперимент [Lyle Graham et al.]: Внутриклеточные измерения patch-clamp
в зрительной коре кошки in vivo. Стимул – движущаяся полоска.
V  20 mV
GABAA : GI 10 nS
AMPA : GE 5 nS
1s

23. Threshold voltage, VT Peak voltage, V P
«Firing-Clamp»
- method of synaptic
conductance estimation
Idea: a patched neuron is
forced to spike with a constant
rate; gE, gI, are estimated from
values of subthreshold voltage
1 ms
and spike amplitude.
τ(V)

25. Conclusions
Dynamic Clamp
• is needed for measuring firing characteristics of neuron
• is needed for estimation input synaptic conductances in-vivo
• helps to create artificial ionic intrinsic or synaptic channels