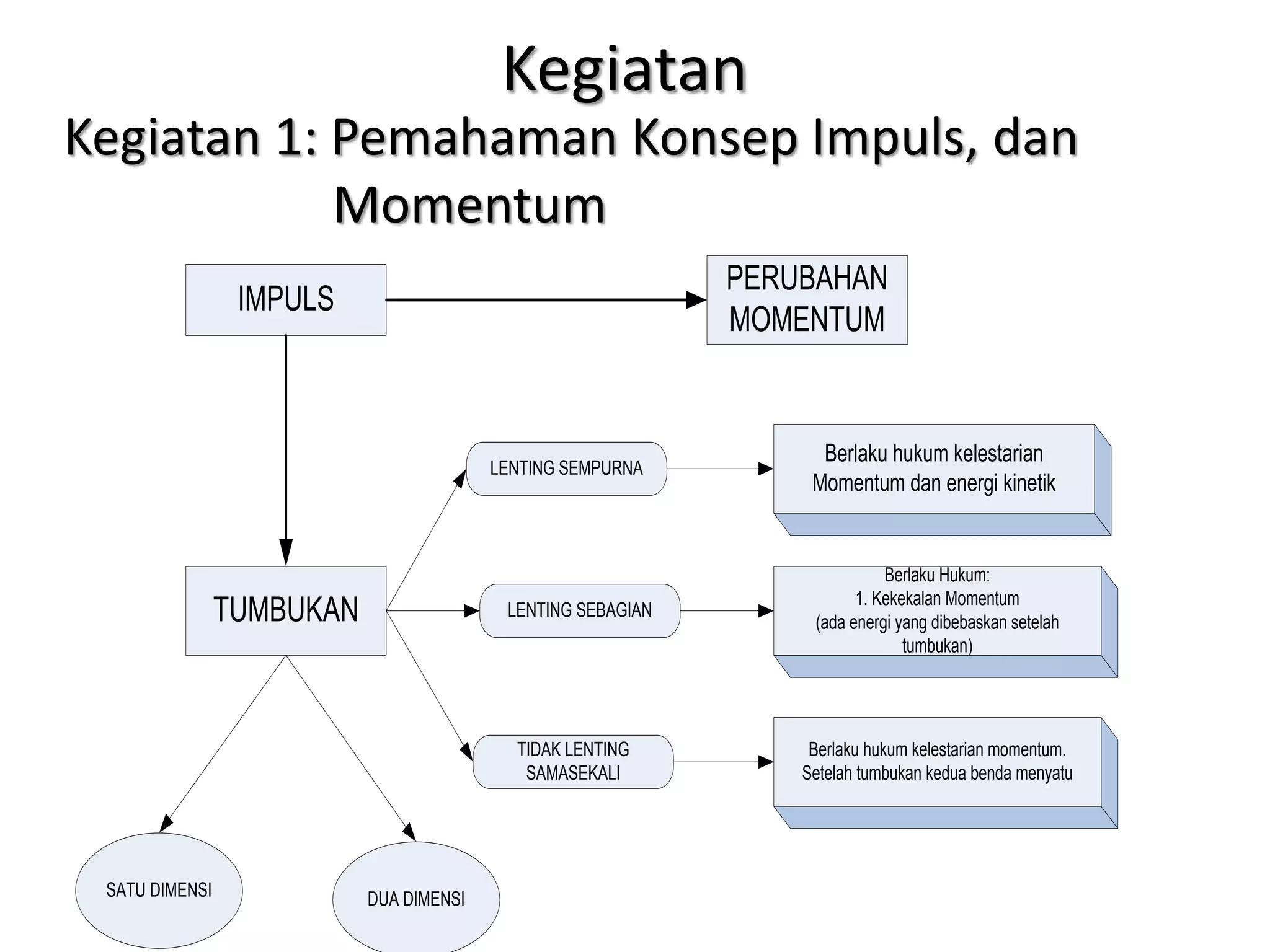
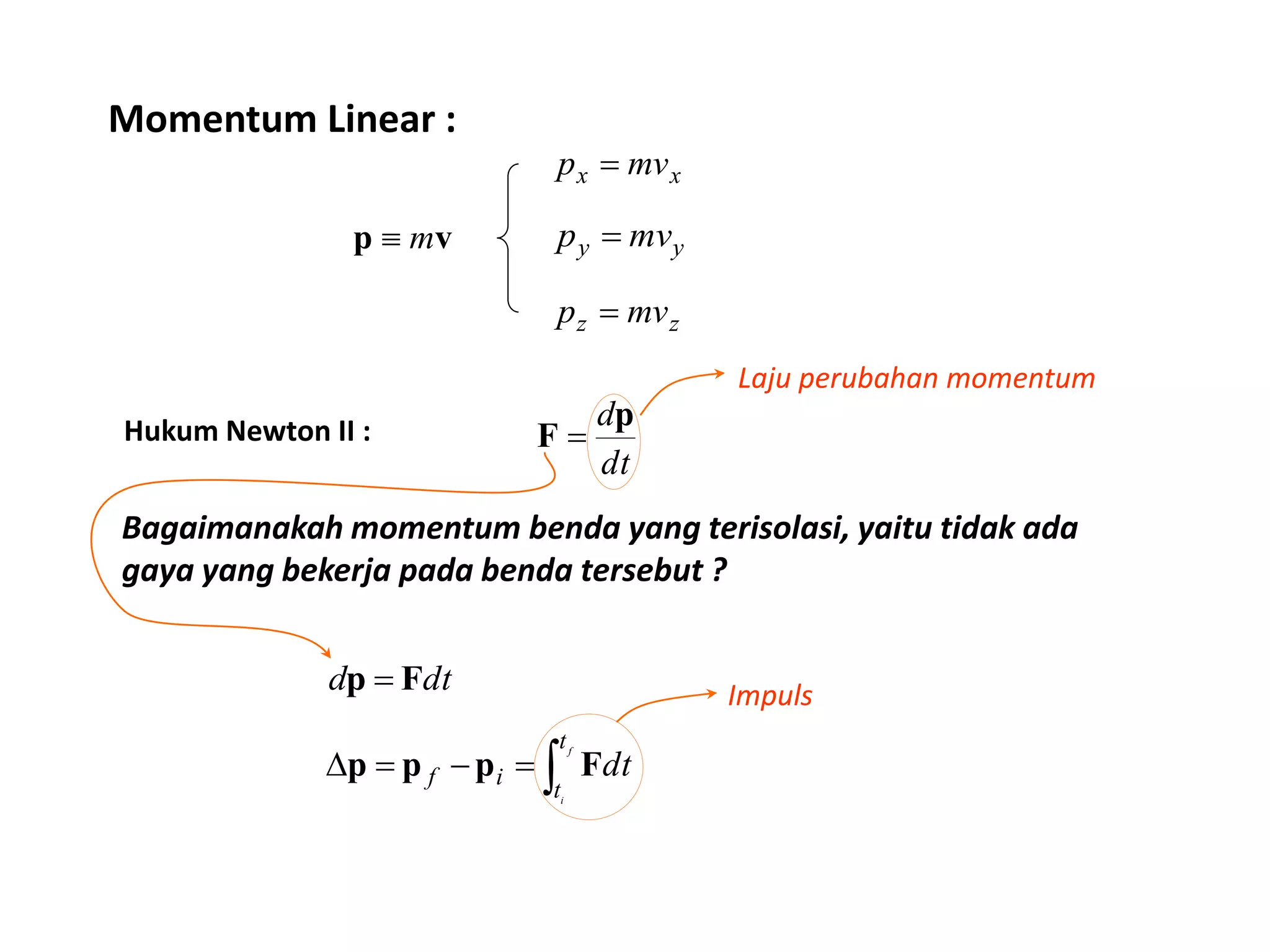
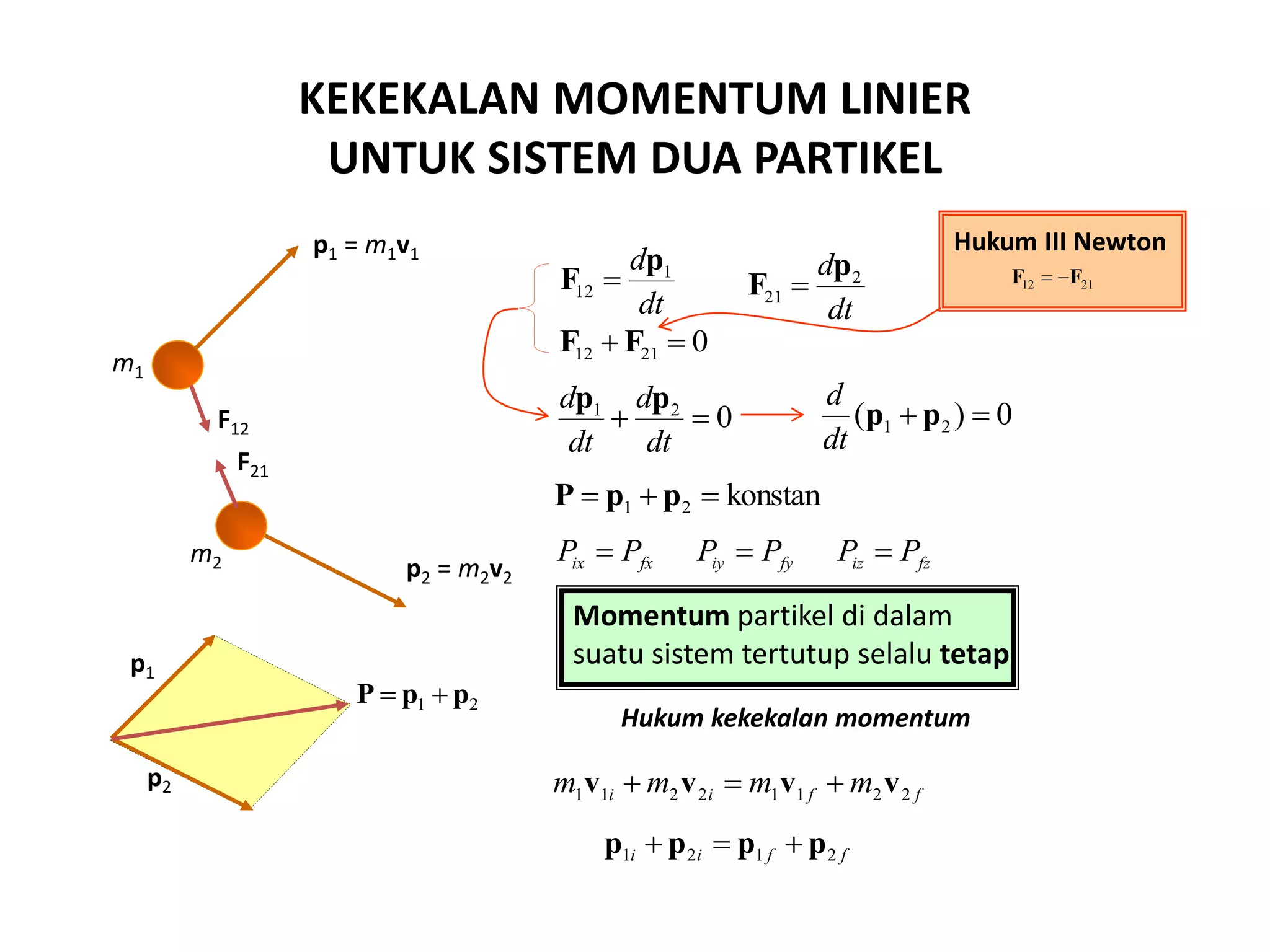
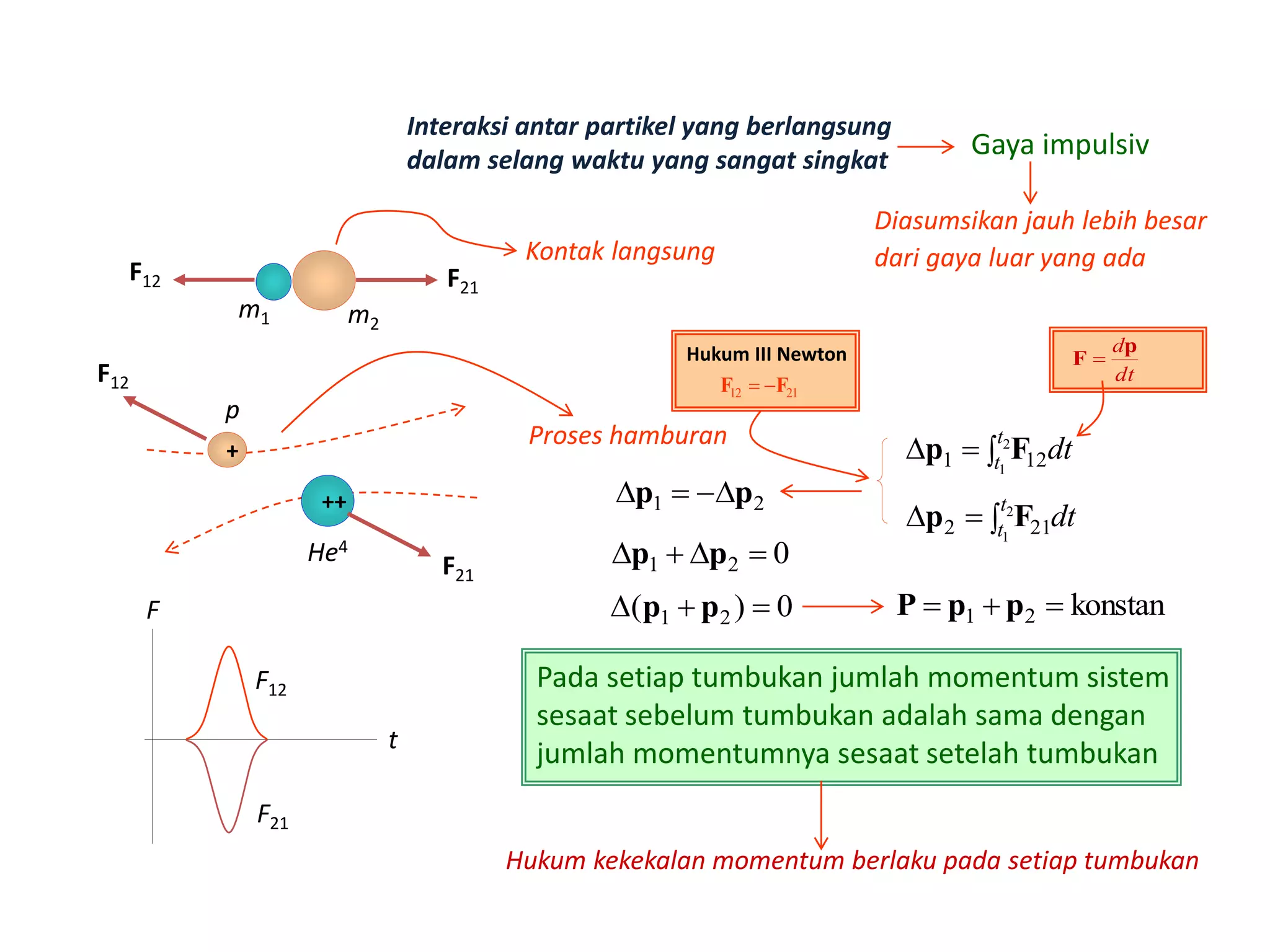
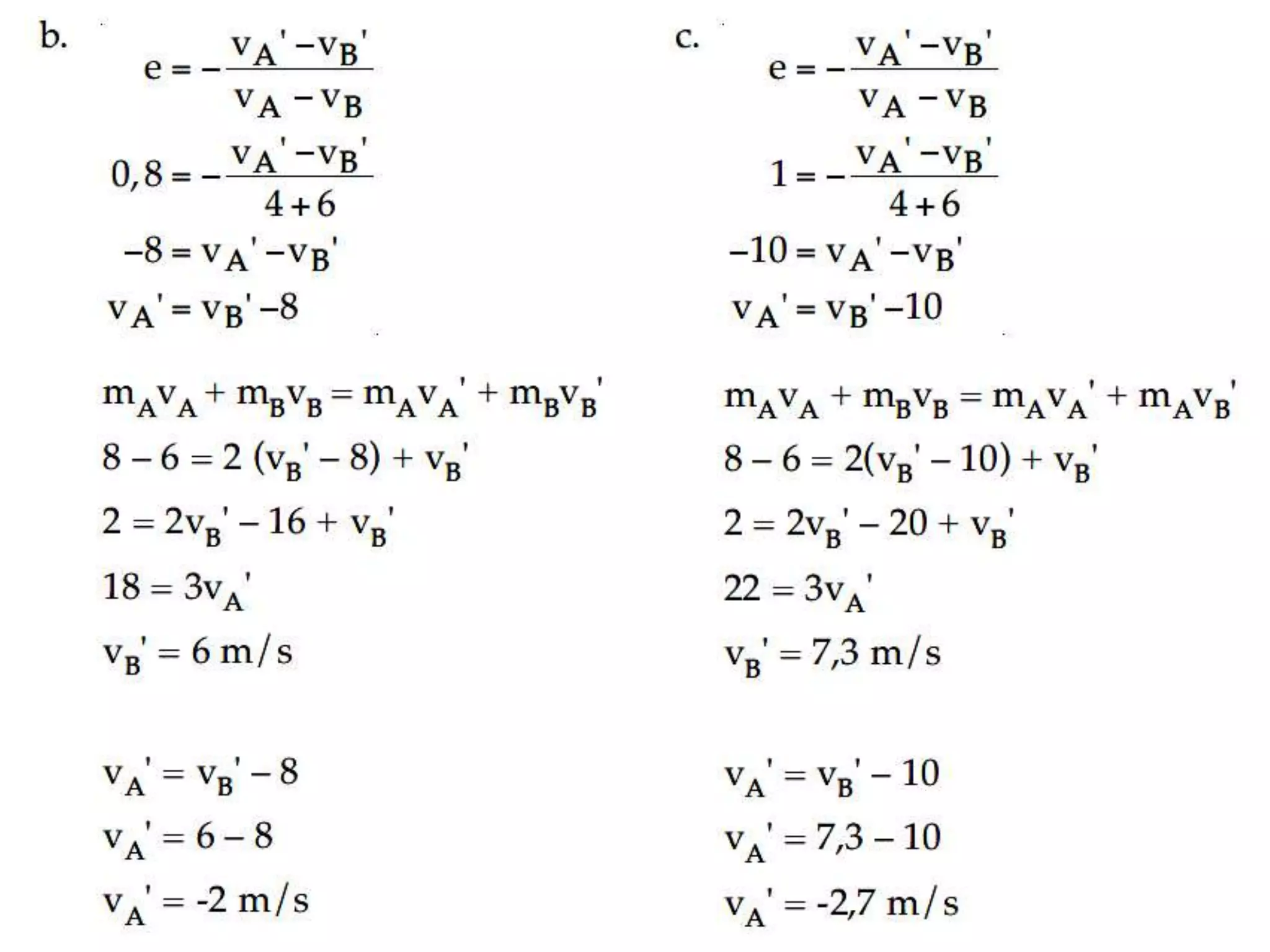Dokumen ini menjelaskan tentang konsep impuls, momentum, dan hukum kekekalan momentum pada berbagai jenis tumbukan, termasuk tumbukan lenting sempurna, lenting sebagian, dan tidak lenting sama sekali. Terdapat penjabaran hukum-hukum fisika yang berlaku serta contoh soal untuk memahami aplikasi teori tersebut dalam situasi nyata. Peserta diharapkan dapat menganalisis fenomena momentum melalui aktivitas yang dijelaskan dalam sesi.

1. Tujuan
Setelah mengikuti sesi ini
(melakukan berbagai aktivitas
santifik) peserta diharapkan mampu:
Menganalisis besaran fisis
pada fenomena momentum
Dr. Pujiyanto, M.Pd

2. Pendahuluan
 Pernahkah kalian
mengamati bagaimana
pemain billiard dan bowling
mengatur strategi untuk
mendapatkan skor tinggi?
 Apa yang dilakukan para
atlit tersebut?

3. Pertanyaan
Bagaimana dampak tumbukan
bola bowling jika didorong &
digerakkan:
 Cepat
 Lambat

4. Kegiatan 1: Pemahaman Konsep Impuls, dan
Momentum
IMPULS
PERUBAHAN
MOMENTUM
TUMBUKAN
LENTING SEMPURNA
TIDAK LENTING
SAMASEKALI
LENTING SEBAGIAN
Berlaku hukum kelestarian
Momentum dan energi kinetik
Berlaku Hukum:
1. Kekekalan Momentum
(ada energi yang dibebaskan setelah
tumbukan)
Berlaku hukum kelestarian momentum.
Setelah tumbukan kedua benda menyatu
SATU DIMENSI DUA DIMENSI
Kegiatan

5. vp m
xx mvp 
yy mvp 
zz mvp 
Hukum Newton II :
dt
dp
F 
Laju perubahan momentum
Bagaimanakah momentum benda yang terisolasi, yaitu tidak ada
gaya yang bekerja pada benda tersebut ?
dtd Fp  Impuls
Momentum Linear :

f
i
t
t
if dtFppp

6. Impuls :
pFI  
f
i
t
t
dt
Impuls suatu gaya F sama dengan
perubahan momentum benda.
Teorema Impuls-Momentum
F
tti tf


f
i
t
t
dt
t
FF
1
Gaya rata-rata :
Untuk F konstan :
t FpI
t FpI

7. KEKEKALAN MOMENTUM LINIER
UNTUK SISTEM DUA PARTIKEL
m1
p1 = m1v1
m2 p2 = m2v2
p1
p2
F21
F12
dt
d 1
12
p
F 
dt
d 2
21
p
F 
02112  FF
2112 FF 
Hukum III Newton
021

dt
d
dt
d pp
0)( 21  pp
dt
d
konstan21  ppP
fxix PP  fyiy PP  fziz PP 
21 ppP 
Momentum partikel di dalam
suatu sistem tertutup selalu tetap
Hukum kekekalan momentum
ffii mmmm 22112211 vvvv 
ffii 2121 pppp 

8. HUKUM KEKEKALAN MOMENTUM LINIER
Bila benda dengan massa m bergerak karena pengaruh gaya
konstan F, sehingga timbul percepatan sebesar a maka berdasar
hukum II Newton diperoleh
persamaan:
F. Δt disebut impuls gaya yang bekerja pada suatu benda selama
Δt.

10. Contoh Soal
Sebuah mobil dengan massa 200 kg sedang bergerak dengan
kecepatan 72 km/jam (20 m/det), kemudian dipercepat dengan
gaya konstan sehingga dalam waktu 5 sekon kecepatanya
menjadi 80 km/jam (22,2 m/det).
Tentukan:
a. momentum mobil sebelum dipercepat
b. impuls gaya selama 5 sekon tersebut!
Penyelesaian
a). Momentum awal po = m . vo
po = 200 x 20 = 4000 kg m/det
b). Impuls = momentum
I = m(vt – vo)
I = 200(22,2 - 20)
I = 440 kg m/det

11. KEKEKALAN MOMENTUM
Dua buah bola yang masing-masing
bermassa m1 dan m2 bergerak dengan
kecepatan v1 dan v2.
Kemudian kedua benda bertum-bukan.
Setelah bertumbukan kecepatan masing-
masing benda menjadi v1’ dan v2’.
Karena tidak ada gaya luar yang bekerja pada sistem tersebut,
maka momentum sistem kekal, artinya momentum sebelum dan
sesudah tumbukan sama.
p sebelum tumbukan = p sesudah tumbukan (HK Kekekalan
Momentum)

12. ROKET
Misalkan mula-mula kecepatan roket v dan massa roket m, roket
menyemburkan gas sejumlah Δm, sehingga kecepatan bertambah menjadi
v + Δv.
Kecepatan semburan gas anggap sebesar vg (Catatan: kecepatan roket
dan kecepatan gas diukur relatif terhadap suatu acuan, misalnya bumi).
Momentum mula-mula roket: mv
Momentum akhir roket: (m – Δm) (v + Δv)
Momentum gas: -Δmvg

13. Jika gravitasi diabaikan,maka besarnya pertambahan kecepatan Δv
adalah :
pawal = pakhir
mv = (m – Δm) (v + Δv) – Δmvg
mv = mv – Δm.v + m.Δv – Δm . Δv – Δmvg
Δm . Δv diabaikan karena kecil
0 = -Δm . v + m . Δv – Δmvg
Percepatan roket :
v + vg adalah sama dengan kecepatan roket relatif terhadap gas dan
sering ditulis vr sehingga persamaan percepatan rata-rata roket adalah:
bila percepatan gravitasi tidak diabaikan

14. Contoh Soal
Sebuah roket menembakkan bahan bakar dengan laju 14.000 kg tiap
detik. Hitung percepatan roket ketika kecepatannya 2000 m/det relatif
terhadap gas dan massa roket ketika itu adalah 1000 ton. Jika:
a) medan gravitasi diabaikan.
b) besarnya percepatan akibat gravitasi ditempat itu g = 5 m/det2
Penyelesaian :
a) Percepatan gravitasi g = 0,
b) Medan gravitasi tidak diabaikan g = 5 m/s2. Percepatan roket dapat
dihitung dari hasil a dikurangi dengan percepatan akibat gravitasi ini.
at = a – g
= 28 – 5
= 23 m/det2

15. v1
v2
v1
1
v2
2
F21
F12
Kegiatan 2 Pemahaman Konsep Materi Tumbukan

16. 1. Tumbukan Lenting Sempurna
Pada tumbukan lenting sempurna tidak terdapat kehilangan energi,
sehingga pada tumbukan lenting sempurna:
- berlaku hukum kekekalan energi kinetik
- berlaku hukum kekekalan momentum
m1v1 + m2v2 = m1v1' + m2v2'
- koefisien restitusi: atau
e = 1
12
!
1
!
2
vv
vv
e




17. 2. Tumbukan Lenting Sebagian
Pada tumbukan lenting sebagian terdapat kehilangan energi.
Pada tumbukan lenting sebagian didapat:
- berlaku hukum kekekalan momentum
- koefisien restitusi: 0 < e < 1
3. Tumbukan Tidak Lenting Sama Sekali
Pada tumbukan tidak lenting sama sekali , setelah tumbukan kedua
benda menjadi satu dan bergerak bersama-sama (v1’ = v2’ = v’)
sehingga pada tumbukan tidak lenting sama sekali:
- berlaku hukum kekekalan momentum
m1v1 + m2v2 = (m1 + m2)v'
- koefisien restitusi: e = 0

18. +
++
F12
F21
p
He4
F12 F21
m1 m2
Interaksi antar partikel yang berlangsung
dalam selang waktu yang sangat singkat
Gaya impulsiv
Diasumsikan jauh lebih besar
dari gaya luar yang adaKontak langsung
Proses hamburan
F
t
F12
F21
 2
1
212
t
t dtFp
dt
dp
F 
 2
1
121
t
t dtFp
2112 FF 
Hukum III Newton
21 pp 
021  pp
0)( 21  pp konstan21  ppP
Pada setiap tumbukan jumlah momentum sistem
sesaat sebelum tumbukan adalah sama dengan
jumlah momentumnya sesaat setelah tumbukan
Hukum kekekalan momentum berlaku pada setiap tumbukan

19. Klasifikasi Tumbukan
Tumbukan Lenting Sempurna Berlaku hukum kekekalan momentum
dan kekekalan energi
Tumbukan Lenting Sebagian Energi mekanik berkurang
(tak berlaku hukum kekekalan energi mekanik)
Tumbukan Tak Lenting sama sekali Setelah tumbukan kedua partikel menyatu
v1iv2i
m1m2
Sebelum tumbukan
vf
m1 + m2
Setelah tumbukan
Hukum kekekalan momentum :
Untuk tumbukan tak lenting sama sekali dalam satu dimensi
fii vmmvmvm )( 212211  (9-13)
21
2211
mm
vmvm
v ii
f


 (9-14)

20. Untuk tumbukan lenting sempurna dalam satu dimensi
v1iv2i
m1m2
Sebelum tumbukan
v1f
m1
Setelah tumbukan
m2
v2f
Hukum kekekalan momentum :
ffii vmvmvmvm 22112211  (9-15)
2
222
12
112
12
222
12
112
1
ffii vmvmvmvm  (9-16)
)()( 2
2
2
22
2
1
2
11 iffi vvmvvm 
))(())(( 2222211111 ififfifi vvvvmvvvvm  (9-17)
)()( 222111 iffi vvmvvm  (9-18)
iffi vvvv 2211 
)( 2121 ffii vvvv  (9-19)
















21
12
1
21
1
2
2
mm
mm
v
mm
m
v if
(9-21)
















21
2
1
21
21
1
2
mm
m
v
mm
mm
v if (9-20)

21. TUMBUKAN DALAM DUA DIMENSI
v1i
m1
m2
Sebelum tumbukan Setelah tumbukan
v1f
v2f
m1
m2
q
f
v1f sin q
v1f cos q
v2f cos f
-v2f sin f
Komponen ke arah x : fq coscos 221111 ffi vmvmvm  (9-24a)
fq sinsin0 2211 ff vmvm  (9-24b)
Jika tumbukan lenting sempurna : 2
222
12
112
12
112
1
ffi vmvmvm  (9-24a)

22. Contoh Soal
Sebuah peluru dengan massa 20 gram ditembakkan dengan
senapan yang bermassa 2 kg. Jika kecepatan peluru saat
meninggalkan moncong senapan = 10 m/s, maka berapakah
kecepatan senapan setelah menembakkan peluru?
Penyelesaian

23. Contoh soal
Bola A dan bola B bergerak di atas bidang datar segaris kerja. Bola A
dengan massa 2 kg bergerak ke kanan dengan kecepatan 4 m/s dan
bola B dengan massa 1 kg bergerak ke kiri dengan kecepatan 6 m/s.
Kedua bola bertumbukan sentral. Hitunglah kecepatan masing-
masing bola setelah tumbukan jika tumbukan kedua bola:
a. tidak lenting sama sekali
b. lenting sebagian dengan e = 0,8
c. lenting sempurna

25. Soal
Gambar di samping melukiskan
sebuah balok yang bermassa 5 kg
terletak di atas lantai kasar dengan
koefisien gesek = 0,4. Sebuah peluru
dengan massa 50 gram bergerak
dengan kecepatan 80 m/s kemudian
mengenai balok.
Tentukan berapakah jauh balok dapat bergerak jika:
a. peluru dipentalkan kembali oleh balok dengan kecepatan 10 m/s
b. peluru bersarang dalam balok
Kerjakan soal tersebut di atas dan kumpulkan pada pertemuan yang
akan datang sebagai tugas !

26. Reflection
• Apa yang telah saudara pahami?
• Apa yang belum saudara pahami?