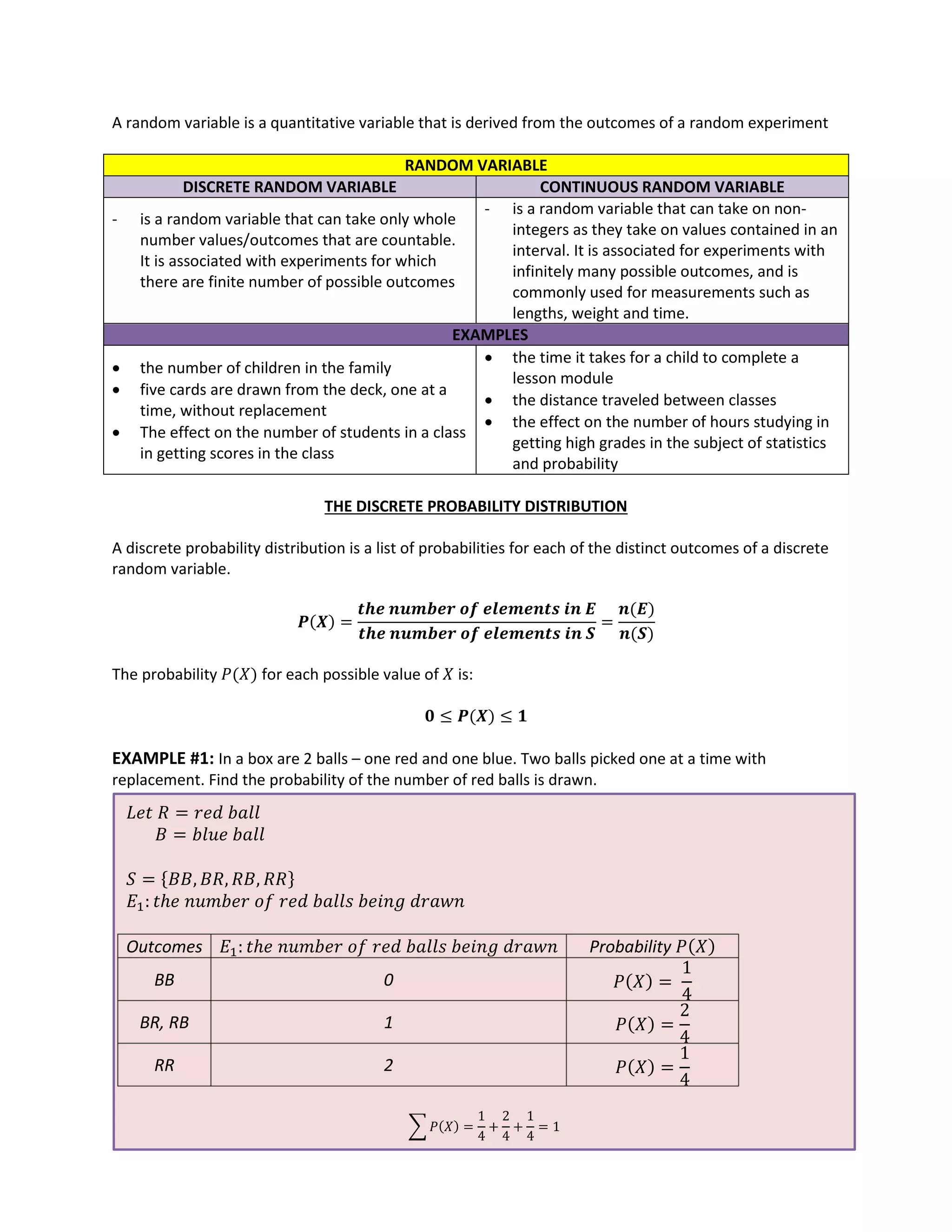
A random variable is a variable that can take on a set of possible values based on the outcome of a random experiment. There are two types of random variables: discrete and continuous. Discrete random variables take on countable whole number values, like the number of children in a family. Continuous random variables take on any real number value within an interval, like time or distance. A discrete probability distribution lists the probability of each possible outcome for a discrete random variable. It assigns a probability value to each outcome. Examples are given of finding the probability of drawing red balls from a box with red and blue balls.

1. A random variable is a quantitative variable that is derived from the outcomes of a random experiment
RANDOM VARIABLE
DISCRETE RANDOM VARIABLE CONTINUOUS RANDOM VARIABLE
- is a random variable that can take only whole
number values/outcomes that are countable.
It is associated with experiments for which
there are finite number of possible outcomes
- is a random variable that can take on non-
integers as they take on values contained in an
interval. It is associated for experiments with
infinitely many possible outcomes, and is
commonly used for measurements such as
lengths, weight and time.
EXAMPLES
 the number of children in the family
 five cards are drawn from the deck, one at a
time, without replacement
 The effect on the number of students in a class
in getting scores in the class
 the time it takes for a child to complete a
lesson module
 the distance traveled between classes
 the effect on the number of hours studying in
getting high grades in the subject of statistics
and probability
THE DISCRETE PROBABILITY DISTRIBUTION
A discrete probability distribution is a list of probabilities for each of the distinct outcomes of a discrete
random variable.
( )
( )
( )
The probability ( ) for each possible value of is:
( )
EXAMPLE #1: In a box are 2 balls – one red and one blue. Two balls picked one at a time with
replacement. Find the probability of the number of red balls is drawn.
𝐿𝑒𝑡 𝑅 𝑟𝑒𝑑 𝑏𝑎𝑙𝑙
𝐵 𝑏𝑙𝑢𝑒 𝑏𝑎𝑙𝑙
𝑆 *𝐵𝐵, 𝐵𝑅, 𝑅𝐵, 𝑅𝑅+
𝐸1: 𝑡ℎ𝑒 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑟𝑒𝑑 𝑏𝑎𝑙𝑙𝑠 𝑏𝑒𝑖𝑛𝑔 𝑑𝑟𝑎𝑤𝑛
𝑃(𝑋)
1
4
+
2
4
+
1
4
1
Outcomes 𝐸1: 𝑡ℎ𝑒 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑟𝑒𝑑 𝑏𝑎𝑙𝑙𝑠 𝑏𝑒𝑖𝑛𝑔 𝑑𝑟𝑎𝑤𝑛 Probability 𝑃(𝑋)
BB 0 𝑃(𝑋)
1
4
BR, RB 1 𝑃(𝑋)
2
4
RR 2 𝑃(𝑋)
1
4

2. EXAMPLE #2: In the random experiment in example #1, what is the probability that at least 1 red ball
can be drawn.
𝐿𝑒𝑡 𝑅 𝑟𝑒𝑑 𝑏𝑎𝑙𝑙
𝐵 𝑏𝑙𝑢𝑒 𝑏𝑎𝑙𝑙
𝑆 *𝐵𝐵, 𝐵𝑅, 𝑅𝐵, 𝑅𝑅+
𝐸1: 𝑎𝑡 𝑙𝑒𝑎𝑠𝑡 𝑜𝑛𝑒 𝑟𝑒𝑑 𝑏𝑎𝑙𝑙 𝑖𝑠 𝑑𝑟𝑎𝑤𝑛
𝐸1 *𝐵𝑅, 𝑅𝐵, 𝑅𝑅+
𝑃(𝑋)
𝑛(𝐸)
𝑛(𝑆)
3
4
0.75 → 𝑡ℎ𝑒 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦