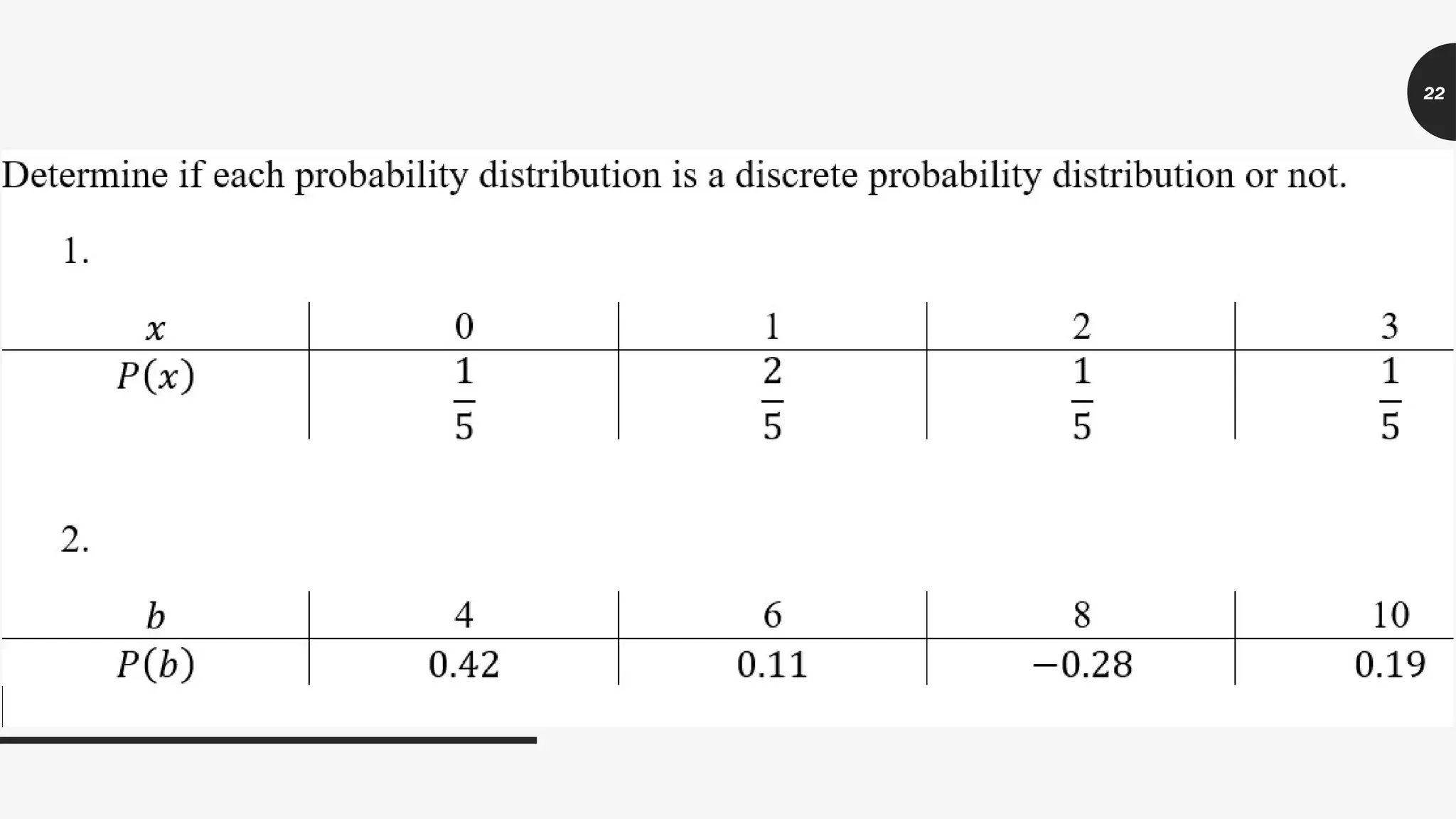
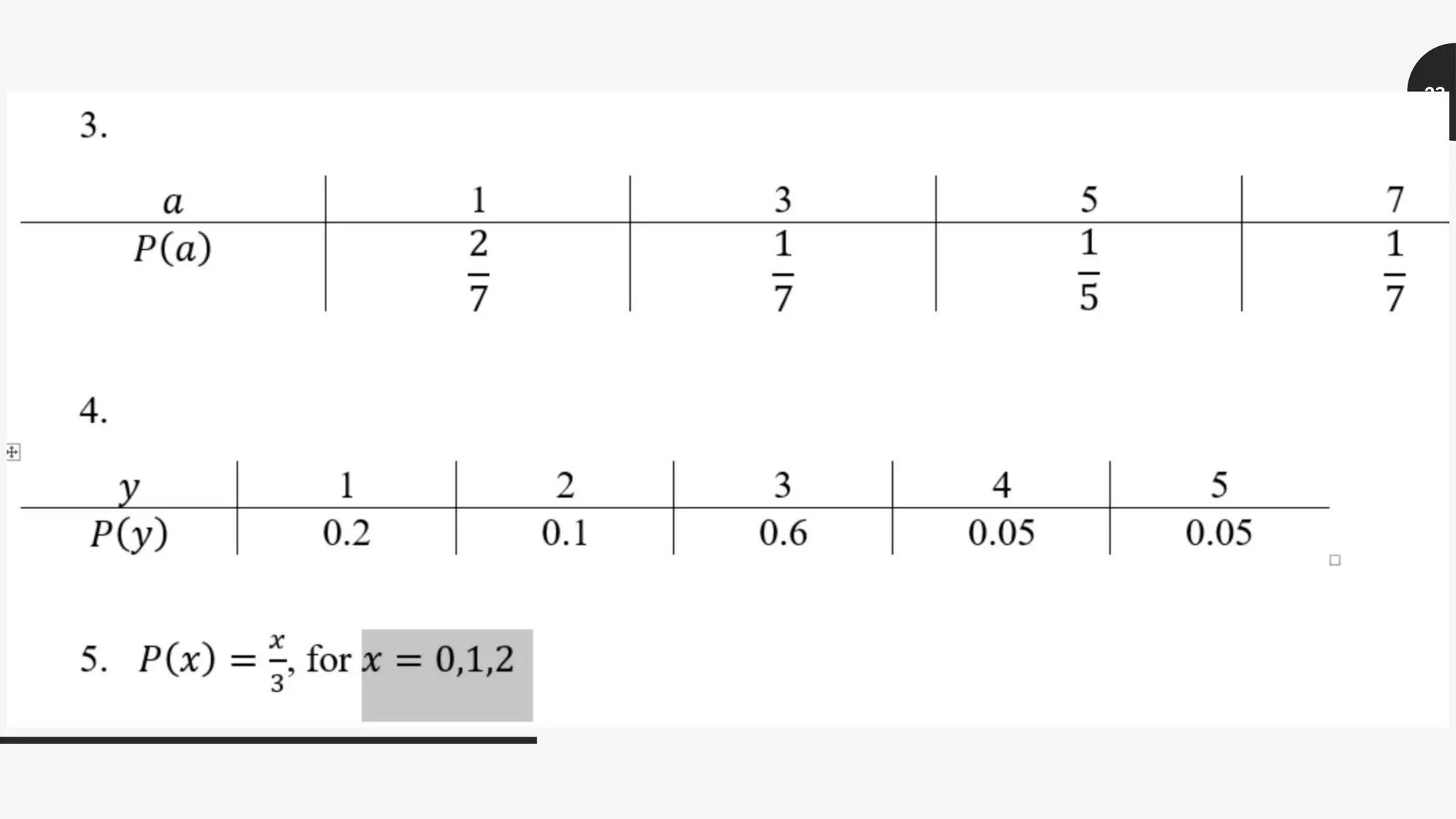
The document explains the concept of random variables, detailing their definition, types (discrete and continuous), and examples of each. It distinguishes discrete random variables, which can be represented by whole numbers from finite or countably infinite outcomes, from continuous random variables, which arise from measurements and cannot be represented as whole numbers. Additionally, the document presents the concept of discrete probability distributions, including properties and examples.

1. 1
RANDOM
VARIABLE
Paul Jorel R. Santos

2. Random
Variable
In some experiments
such as tossing a coin
three times, rolling a
die twice, drawing two
balls from an urn and
the like, few are not
oftentimes concerned
with every detail of the
outcomes.
1

3. Random
Variable
We are usually
interested in some
numerals associated
with the outcomes.
For instance, if a coin
is tossed twice, the
set of all possible
outcomes (S) of the
experiment is:
2
𝑆={𝑇𝑇,𝑇𝐻,𝐻𝑇,𝐻𝐻}

4. Random
Variable
If we are interested in
the number of tails
that came out in the
experiment, then we
can assign numbers
0, 1, and 2 for each of
the 4 possible
outcomes. Thus, we
can write
𝑆={𝑇𝑇,𝑇𝐻,𝐻𝑇,𝐻𝐻}

5. Sample
Space
Number of
Tails
TT 2
TH 1
HT 1
HH 0
From the table on the
left, instead of writing
Number of Tails, we
can denote it as set X
whose elements are
0, 1 and 2. In
symbol, . Then, X is
called a random
variable.

6. Definition
A random variable is a set whose elements are
the numbers assigned to the outcomes of an
experiment. It is usually denoted by uppercase
letters such as X, whose elements are denoted
by lower case letters, and so on.
2

7. Types of Random Variables
In an experiment of tossing a coin times, if X is
the random variable determined by the number
of tails that will come out, then there is always a
whole number (e.g. 0,1,2,…,n) that could be
associated with each outcome, regardless of
whether is finite (countable) or infinite as the
number of whole numbers. This type of random
variable is called discrete random variable.
2

8. Types of Random Variables
However, in a random variable , determined by
weight of students (in kg) in any given moment,
it is impossible for us to assign a whole number
for each weight, because between two weights,
there is always another value of weight. This is
called a continuous random variable.
2

9. Definition
A random variable is said to be discrete
random variable if it has a finite number of
elements or infinite but can be represented by
whole numbers. These values usually arise from
counts.
2

10. Definition
A random variable is said to be continuous
random variable if it has infinite number of
elements or infinite but cannot be represented
by whole numbers. These values usually arise
from measurements.
2

11. Example 1
A teacher’s record has the following (a) scores of
student in a 50-item test, (b) gender, (c) height of the
students.
Let
Classify each variable above as discrete or continuous.
2

12. Example 1: Answer
X is discrete random variable because the scores of
the students are represented by whole numbers.
Y is also a discrete random variable because male
and female could be coded and , and, could be counted.
Z is continuous random variable because between
two values of height, there are always infinite number of
possible values for height thus making representations
to be impossible
2

13. Practice Exercise
2

14. Practice Exercise
6. The number of bread baked each day.
7. The air temperature in a city yesterday.
8. The income of single parents living in Quezon
City.
9. The weights of newborn infants.
10. The capacity (in liters) of water in a swimming
pool.
2

15. Probability
Distribution
In the experiment of
tossing a coin twice,
there are four possible
outcomes namely: HH,
HT, TH and TT. If X is a
random variable
representing the
number of tails in the
outcomes, then:
1
𝑋={0,1,2}

16. Probability
Distribution
)

17. Definition
A discrete probability distribution is a table
showing all the possible values of a discrete
random variable together with their
corresponding probabilities.
2

18. Properties of Discrete Probability Distribution
If X is a random variable with elements, then
1. Each of the probabilities, , has the value
which range from 0 through 1.
2. The sum of the probabilities,
2

19. Example 1
Is the distribution below a discrete probability
distribution?
2
1 2 3
0.12 0.82 0.06

20. Example 2
Write the probability distribution of a random
variable R representing the number of red balls
when 3 balls are drawn in succession with
replacement from a jar containing 4 red and 4
blue balls.
2
0 1 2
3/8
3
1/8

21. Example 3
Box A and Box B both contain the number 1, 2,
3 and 4. Write the mass function and draw the
histogram of the sum when one number from
each box is taken at a time, with replacement.
2

22. 22

23. 23