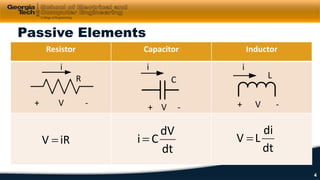
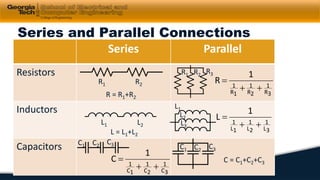
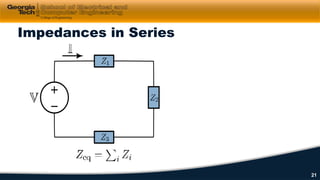
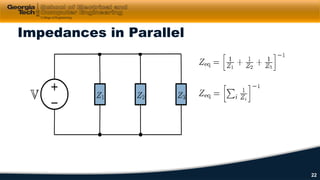
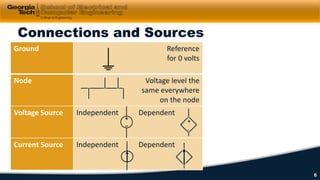
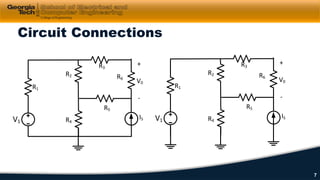
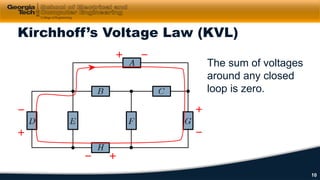
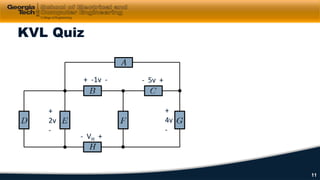
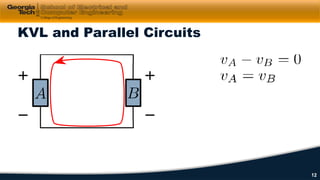
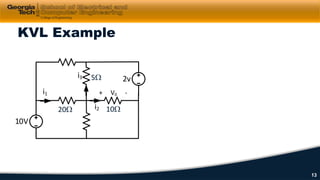
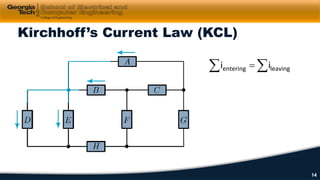
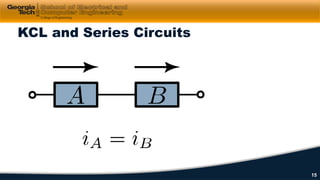
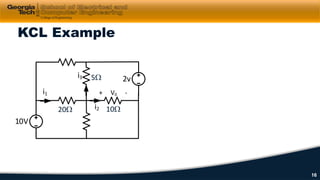
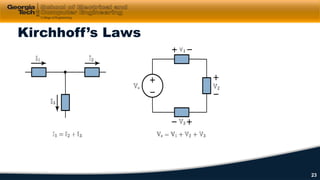
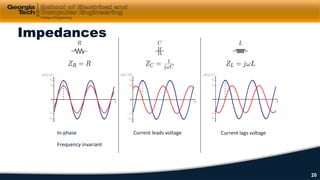
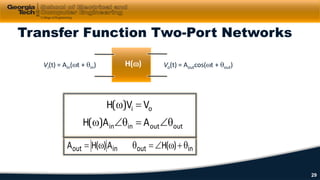
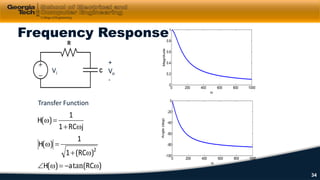
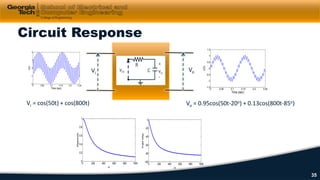
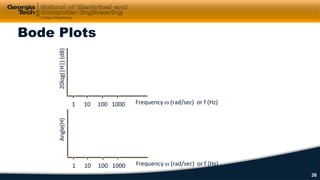
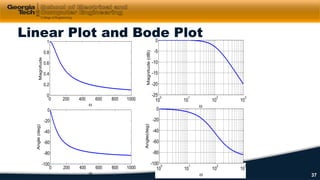
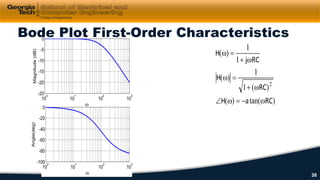
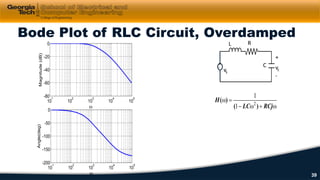
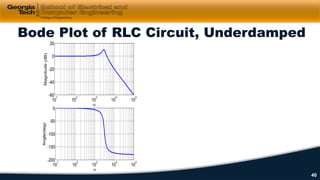
This document provides an overview and review of key concepts in electronics circuits, including: 1) Circuit elements such as resistors, capacitors, and inductors are introduced along with their i-v characteristics and connections in series and parallel. 2) Kirchhoff's laws including Kirchhoff's voltage law (KVL) and Kirchhoff's current law (KCL) are reviewed and applied to example circuits. 3) Impedance, transfer functions, and frequency response plots (Bode plots) are discussed as ways to characterize and analyze AC circuits.

1. School of Electrical and Computer Engineering
Introduction to Electronics
Module 1: Overview and
Background
An introduction to electronic components and a study of circuits
containing such devices.

2. Dr. Bonnie H. Ferri
Professor and Associate Chair
School of Electrical and
Computer Engineering
School of Electrical and Computer Engineering
Review of Circuit
Elements
Review linear circuit components and properties

3.  Review
 Resistors, capacitors, inductors
○ i-v characteristics of these elements
 Sources, nodes
Lesson Objectives
3

4. Passive Elements
Resistor Capacitor Inductor
+ V -
i
R
iRV =
+ V -
C
i
dt
dV
Ci =
+ V -
L
i
dt
di
LV =
4

5. Series and Parallel Connections
Series Parallel
Resistors
Inductors
Capacitors
R1 R2
R = R1+R2
R1 R2
R3
3R
1
2R
1
1R
1
1
R
++
=
3C
1
2C
1
1C
1
1
C
++
=
C1 C2
C3
C1 C2 C3
C = C1+C2+C3
3L
1
2L
1
1L
1
1
L
++
=
L = L1+L2
L1 L2
L1
L2
L3

6. Connections and Sources
Ground Reference
for 0 volts
Node Voltage level the
same everywhere
on the node
Voltage Source Independent Dependent
Current Source Independent Dependent
+
-
6

7. Circuit Connections
V1
R1
R2
R3
R4
R5
+
V0
-
R6
IS V1
R1
R2
R3
R4
R5
+
V0
-
R6
IS
7

8. Dr. Bonnie H. Ferri
Professor and Associate Chair
School of Electrical and
Computer Engineering
School of Electrical and Computer Engineering
Review of
Kirchoff’s Laws
Review of KVL and KCL

9.  Review
 Kirchhoff’s Current Law (KCL)
 Kirchhoff’s Voltage Law (KVL)
Lesson Objectives
9

10. Kirchhoff’s Voltage Law (KVL)
The sum of voltages
around any closed
loop is zero.
10

11. KVL Quiz
+
2v
-
+
4v
-
- 5v ++ -1v -
- VH +
11

12. KVL and Parallel Circuits
12

13. KVL Example
10V
2v
+ V0 -i1
i2
i3
20Ω 10Ω
5Ω
13

14. Kirchhoff’s Current Law (KCL)
∑ ∑= leavingentering ii
14

15. KCL and Series Circuits
15

16. KCL Example
10V
2v
+ V0 -i1
i2
i3
20Ω 10Ω
5Ω
16

17.  Introduced KVL and KCL
 Applied KVL to parallel elements
 Applied KCL to series elements
 Solved a simple circuit using
Kirchhoff’s Laws
Summary
17

18. Dr. Bonnie H. Ferri
Professor and Associate Chair
School of Electrical and
Computer Engineering
School of Electrical and Computer Engineering
Review of
Impedance
Review of Impedance for Analyzing AC Circuits

19.  Review
 Impedances for steady-state sinusoidal inputs (AC)
Lesson Objectives
19

20. Impedances
In-phase Current leads voltage Current lags voltage
Frequency invariant
20

21. Impedances in Series
21

22. Impedances in Parallel
22

23. Kirchhoff’s Laws
23

24. Series RC
+
Vo
-
Vi
24

25. Series RLC
Vi
+
Vo
-
25

26.  Introduced KVL and KCL
 Applied KVL to parallel elements
 Applied KCL to series elements
 Solved a simple circuit using
Kirchhoff’s Laws
Summary
26

27. Dr. Bonnie H. Ferri
Professor and Associate Chair
School of Electrical and
Computer Engineering
School of Electrical and Computer Engineering
Review of
Transfer Functions
Review of transfer functions for characterizing circuits

28.  Review transfer functions
 To characterize a circuit
 To find frequency response curves
Lesson Objectives
28

29. Transfer Function Two-Port Networks
Vi(t) = Ain(ωt + θin) H(ω) Vo(t) = Aoutcos(ωt + θout)
inoutinout )(HA)(HA θ+ω∠=θω=
outoutinin
oi
AAH
VVH
θ∠=θ∠ω
=ω
)(
)(
29

30. Summary of Simple Circuits
jRC1
1
H
ω+
=ω)(
+
Vo
-Vi
+
Vo
-
Vi
+
Vo
-
Vi jRCLC1
1
H 2
ω+ω−
=ω)(
jRC1
jRC
H
ω+
ω
=ω)(
30

31.  Defined transfer function for Two-Port
Networks
 Showed transfer functions of simple circuits
Summary
31

32. Dr. Bonnie H. Ferri
Professor and Associate Chair
School of Electrical and
Computer Engineering
School of Electrical and Computer Engineering
Review of Frequency
Response Plots
(Bode)
Review of linear plots and Bode plots to show the frequency
characteristics of signals and circuits

33.  Define the frequency response for a transfer function
 Show linear plots and Bode plots
Lesson Objectives
)(ωH
Magnitude Plot: |H(ω)| vs ω
Angle Plot: ∠H(ω) vs ω
33

34. Frequency Response
0 200 400 600 800 1000
0
0.2
0.4
0.6
0.8
1
ω
Magnitude
0 200 400 600 800 1000
-100
-80
-60
-40
-20
0
ωAngle(deg)
Transfer Function
)tan()(
)(
)(
)(
ω−=ω∠
ω+
=ω
ω+
=ω
RCaH
RC1
1
H
jRC1
1
H
2
+
Vo
-
Vi
34

35. Circuit Response
Vi
Vo
0 0.05 0.1 0.15 0.2 0.25
-2
-1
0
1
2
Time (sec)
v(t)
0 0.05 0.1 0.15 0.2 0.25
-1.5
-1
-0.5
0
0.5
1
1.5
Time (sec)
v(t)
0 200 400 600 800 1000
0
0.2
0.4
0.6
0.8
1
ω
Magnitude
Vi = cos(50t) + cos(800t) Vo = 0.95cos(50t-20o) + 0.13cos(800t-85o)
0 200 400 600 800 1000
-100
-80
-60
-40
-20
0
ω
Angle(deg)
35

36. Bode Plots
Frequency ω (rad/sec) or f (Hz)1 10 100 1000
Frequency ω (rad/sec) or f (Hz)1 10 100 1000
36

37. Linear Plot and Bode Plot
10
0
10
1
10
2
10
3
-100
-80
-60
-40
-20
0
ω
Angle(deg)
10
0
10
1
10
2
10
3
-25
-20
-15
-10
-5
0
ω
Magnitude(dB)
0 200 400 600 800 1000
-100
-80
-60
-40
-20
0
ω
Angle(deg)
0 200 400 600 800 1000
0
0.2
0.4
0.6
0.8
1
ω
Magnitude
37

38. Bode Plot First-Order Characteristics
10
0
10
1
10
2
10
3
-100
-80
-60
-40
-20
0
ω
Angle(deg)
10
0
10
1
10
2
10
3
-25
-20
-15
-10
-5
0
ω
Magnitude(dB)
)tan()(
)(1
1
)(
1
1
)(
2
RCaH
RC
H
RCj
H
ω−=ω∠
ω+
=ω
ω+
=ω
38

39. Bode Plot of RLC Circuit, Overdamped
10
1
10
2
10
3
10
4
10
5
-80
-60
-40
-20
0
ω
Magnitude(dB)
10
1
10
2
10
3
10
4
10
5
-200
-150
-100
-50
0
ω
Angle(deg)
vs
+
-
vc
C
L
vs
+
-
-
R
ω+ω−
=ω
RCjLC
H
)(
)( 2
1
1
39

40. Bode Plot of RLC Circuit, Underdamped
10
1
10
2
10
3
10
4
10
5
-60
-40
-20
0
20
ω
Magnitude(dB)
10
1
10
2
10
3
10
4
10
5
-200
-150
-100
-50
0
ω
Angle(deg)
40

41.  A is a plot of the transfer function
versus frequency
 The frequency response can be used to determine the
steady-state sinusoidal response of a circuit at different
frequencies
Summary
41