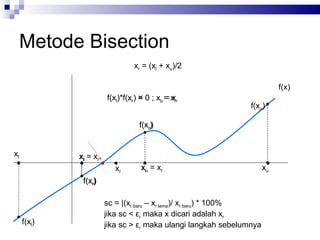
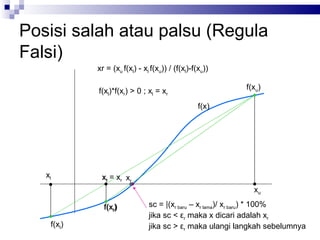
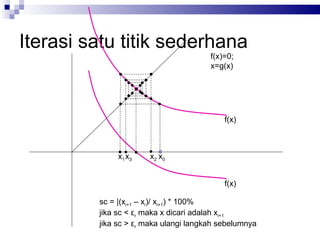
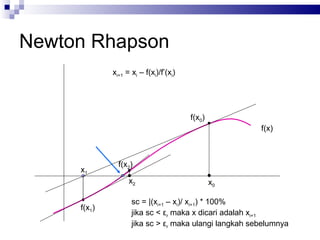
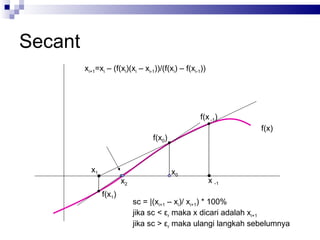
Dokumen tersebut membahas beberapa metode numerik untuk mencari akar persamaan, yaitu metode bisection, regula falsi, iterasi satu titik sederhana, Newton Rhapson, dan Secant. Metode-metode tersebut menggunakan prinsip iterasi untuk mempersempit rentang pencarian akar secara berulang hingga mencapai nilai yang diinginkan.

1. Metode Numerik
Moch. Arif Wicaksono SSi. MT.

2. Mencari akar persamaan
 Metode akolade (tertutup)
 Bisection Method (metoda
bagi dua)
 Posisi Salah atau palsu
 Metode terbuka
 Iterasi satu titik sederhana
 Newton Rhapson
 Secant

3. Metode Bisection
xr = (xl + xu)/2
f(x)
f(xl)*f(xr) < 0 ; xu = xrr
> l = x
f(xu)
f(xru))
xl xrl = xr
xr xru = xr xu
f(xlr)
sc = |(xr baru – xr lama)/ xr baru) * 100%
jika sc < εr maka x dicari adalah xr
f(xl) jika sc > εr maka ulangi langkah sebelumnya

4. Bisection method
Algoritma:
 Tentukan dua buah tebakan awal xl dan xu
 Cari nilai tengah antara xl dan xu, dengan rumusan xr = (xl + xu)/2
 Hitung f(xl) dan f(xr)
 Jika f(xl) * f(xr) > 0 maka xl baru = xr
 Jika f(xl) * f(xr) < 0 maka xu baru = xr
 Ulangi langkah 2 s.d. 5
 Bandingkan harga xr yang lama dengan yang baru
 Jika harga perbandingan (harga kesalahan relatif) sudah lebih
kecil dari yang dinginkan maka harga x (akar persamaan dicari)
adalah harga xr terakhir
 Jika belum memenuhi syarat maka ulangi langkah 1 s.d. 6
sampai syarat no. 7 terpenuhi

5. Posisi salah atau palsu (Regula
Falsi)
xr = (xu f(xl) - xl f(xu)) / (f(xl)-f(xu))
f(xl)*f(xr) > 0 ; xl = xr f(xu)
f(x)
xl xrl = xr xr
xu
f(xlr) sc = |(xr baru – xr lama)/ xr baru) * 100%
jika sc < εr maka x dicari adalah xr
f(xl) jika sc > εr maka ulangi langkah sebelumnya

6. Posisi salah atau palsu
 Cari nilai xr dengan rumus
xr = (xuf(xl)-xlf(xu))/(f(xl)-f(xu))
 Selanjutnya gunakan algoritma bisection

7. Iterasi satu titik sederhana
f(x)=0;
x=g(x)
f(x)
x1 x3 x2 x0
f(x)
sc = |(xi+1 – xi)/ xi+1) * 100%
jika sc < εr maka x dicari adalah xi+1
jika sc > εr maka ulangi langkah sebelumnya

8. Iterasi satu titik sederhana
1. Buat fungsi sehingga menjadi f(x)=0
2. Gunakan aljabar sehingga fungsi menjadi
x = g(x)
4. Ubah fungsi di atas menjadi
xi+1 = g(xi)
 Lakukan iterasi pertama dengan harga xi = harga tebakan awal
 Lakukan iterasi kedua dengan menggunakan harga x yang diperoleh dari
iterasi pertama
 Bandingkan hasil yang diperoleh dari iterasi kedua dgn iterasi pertama
 Jika hasilnya masih di atas dari kesalahan relatif yang dikehendaki ulangi
langkah ke 4 s.d. ke 6
 Jika hasilnya di bawah kesalahan relatif yg dikehendaki akhiri perhitungan
 Hasil akhir adalah nilai x terakhir yang diperoleh

9. Newton Rhapson
xi+1 = xi – f(xi)/f’(xi)
f(x0)
f(x)
f(x2)
x1
x2 x0
sc = |(xi+1 – xi)/ xi+1) * 100%
f(x1)
jika sc < εr maka x dicari adalah xi+1
jika sc > εr maka ulangi langkah sebelumnya

10. Newton Rhapson
 Cari turunan dari f(x)
 Buat tebakan awal xi
 Cari nilai dari f(xi) dan f’(xi)
 Cari nilai xi+1 dengan rumus sbb:
xi+1 = xi – f(xi)/f’(xi)
6. Ulangi langkah 3 dengan harga x yang didapat pada iterasi
pertama
7. Bandingkan nilai x terakhir dengan x sebelumnya
8. Jika kesalahan relatif lebih besar dari yang dikehendaki, ulangi
langkah 3 s.d. 6
9. Jika kesalahan relatif sudah lebih kecil dari yang dikehendaki
berhenti menghitung
10. Nilai x yang dicari adalah nilai x yang terakhir

11. Secant
xi+1=xi – (f(xi)(xi – xi-1))/(f(xi) – f(xi-1))
f(x -1)
f(x)
f(x0)
x1 x0
x2 x -1
f(x1)
sc = |(xi+1 – xi)/ xi+1) * 100%
jika sc < εr maka x dicari adalah xi+1
jika sc > εr maka ulangi langkah sebelumnya

12. Secant
 Tentukan nilai xi dan xi-1
 cari nilai f(xi) dan f(xi-1)
 Cari nilai xi+1 dengan rumus sbb:
xi+1=xi – (f(xi)(xi – xi-1))/(f(xi) – f(xi-1))
5. Lakukan langkah langkah seperti metode
newton rhapson (5 s.d. 9)