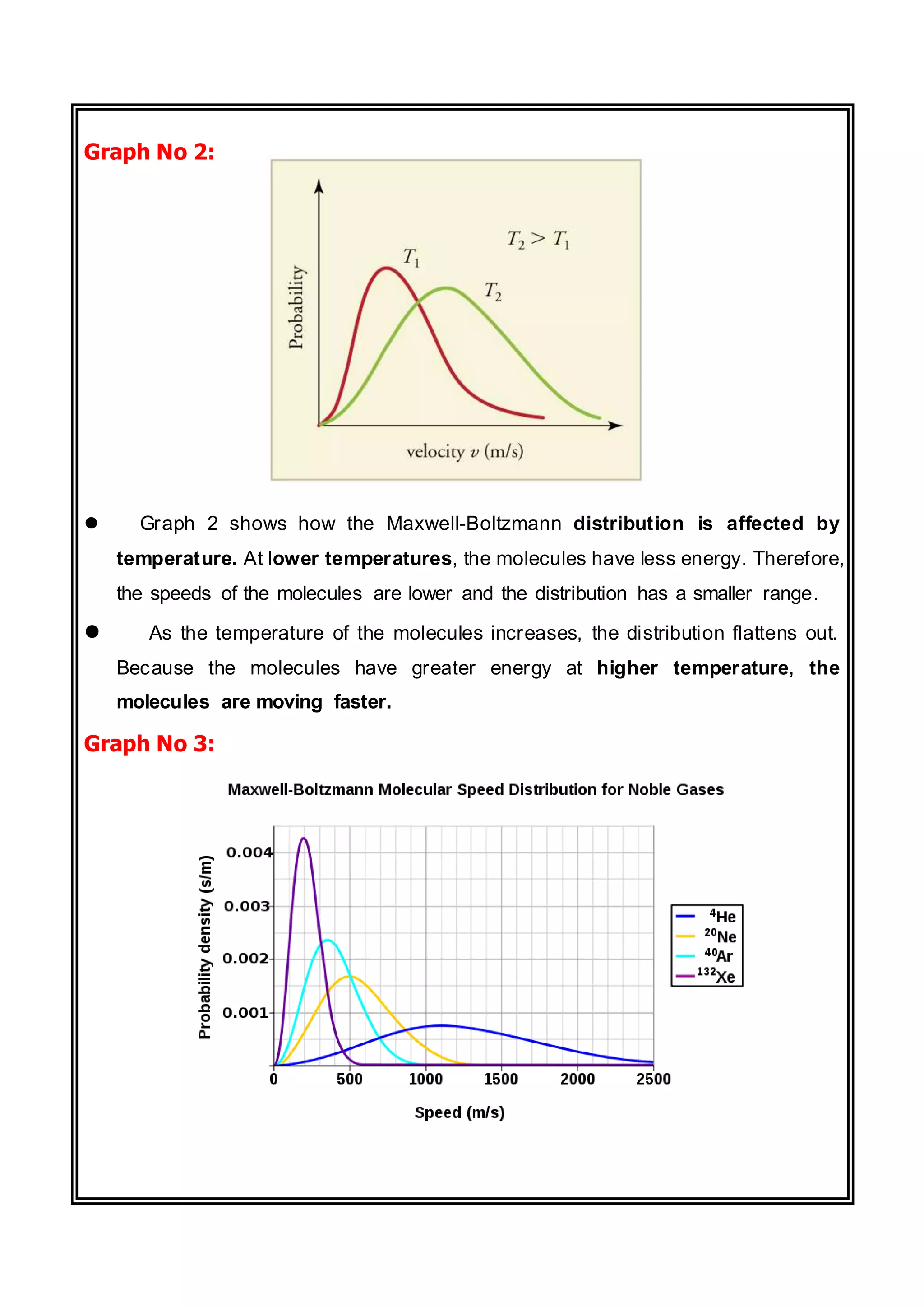
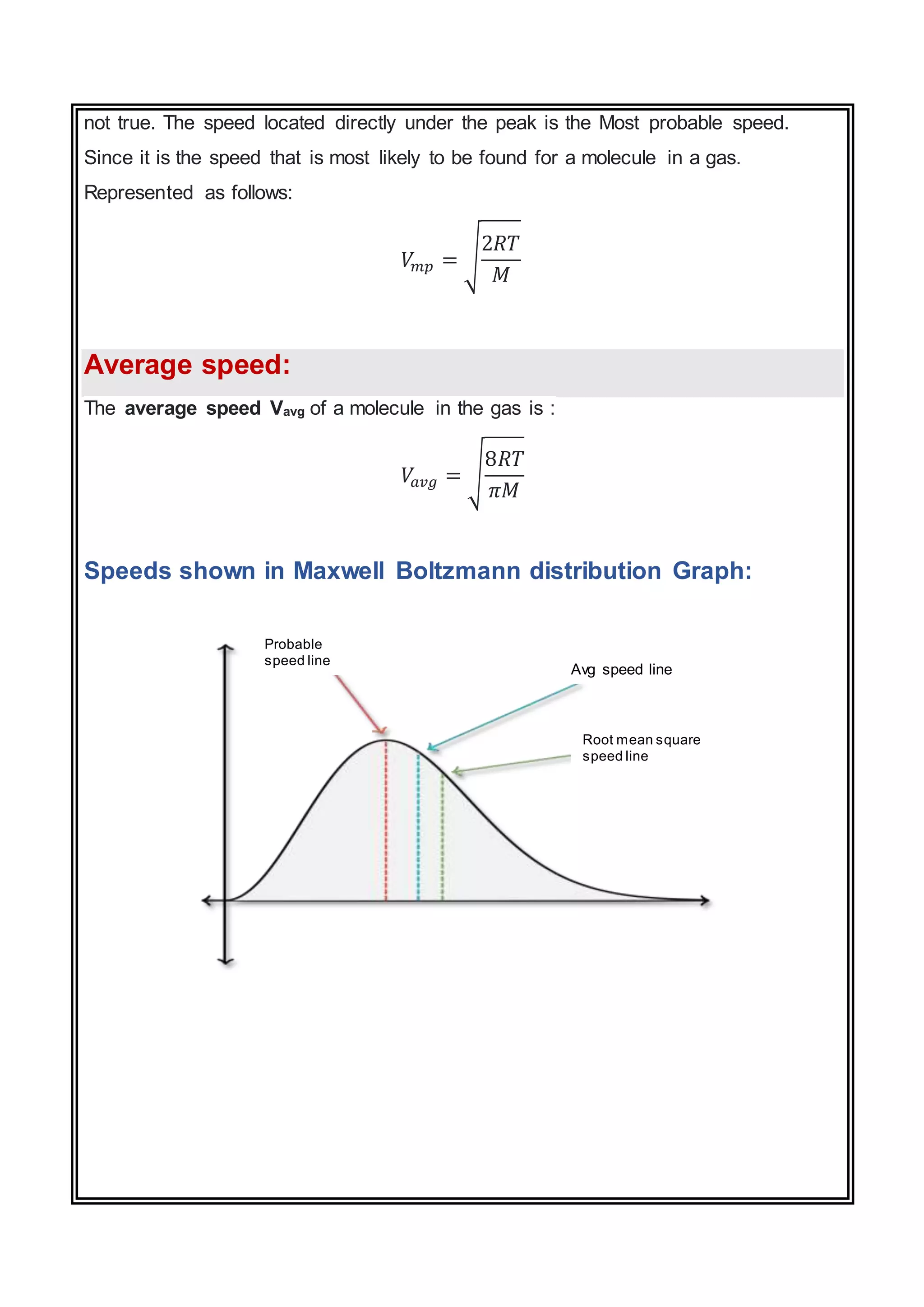
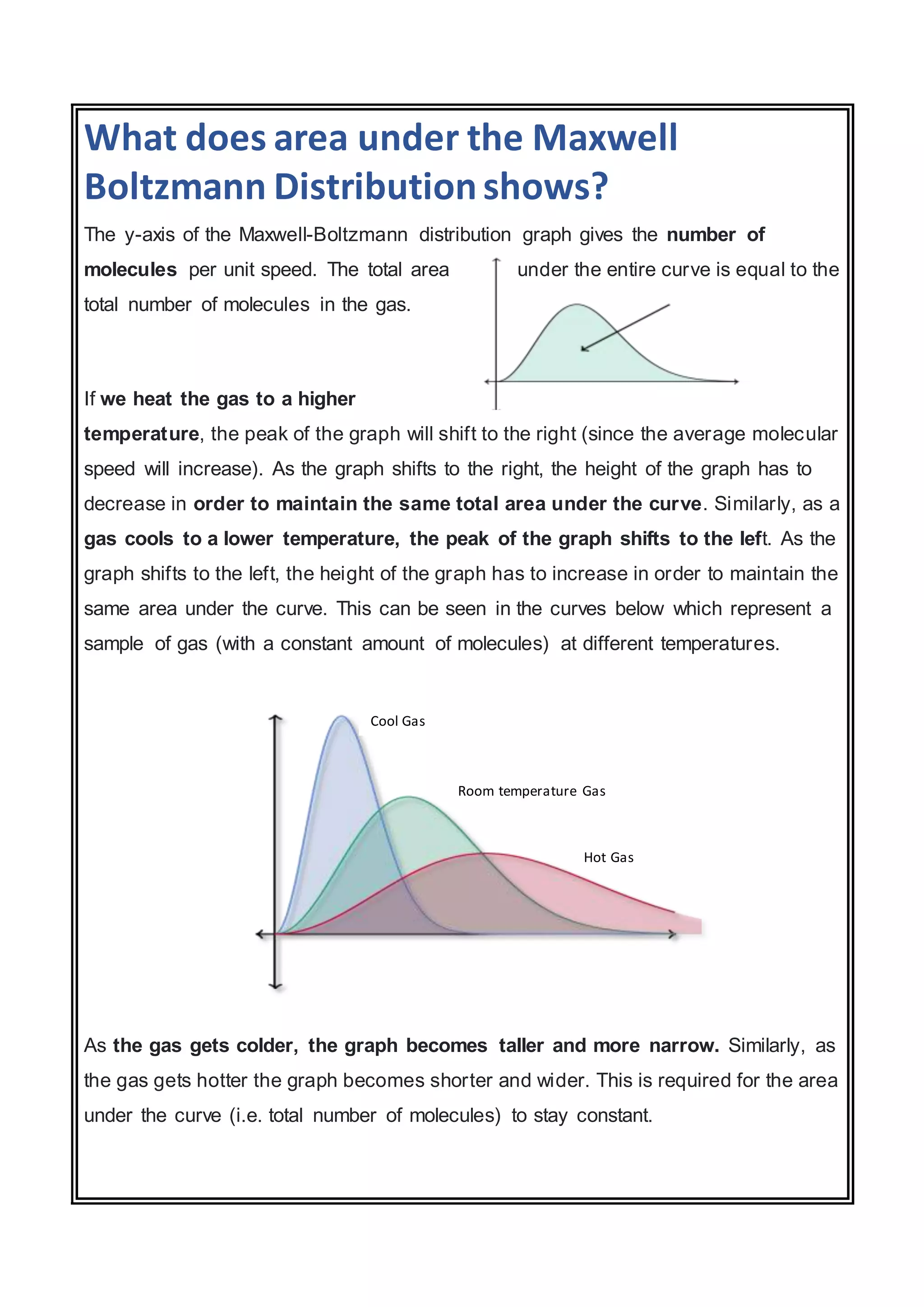
The document discusses the Maxwell-Boltzmann distribution, which describes the speeds of gas molecules at a given temperature. It was first developed by Maxwell and Boltzmann based on probabilistic arguments about molecular velocities. The distribution shows the fraction of molecules moving at different speeds and depends on temperature, mass, and other factors. Graphs of the distribution illustrate how it changes for different temperatures and molecule masses. The root mean square, most probable, and average speeds can be derived from the Maxwell-Boltzmann equation.

1. Physical chemistry
“Maxwell Boltzmann law for distribution of
molecules and molecular velocities”
Semester 5th
The University of Lahore

2. Maxwell Boltzmann law for distribution
of molecules and molecular velocities:
Definition:
A Maxwell-Boltzmann Distribution is a probability distribution used for
describing the speeds of various particles within a stationary container at a
specific temperature. The distribution is often represented with a graph, with
the y-axis defined as the number of molecules and the x-axis defined as
the speed.”
 This distribution was first set forth by the Scottish physicist
James Clerk Maxwell in 1859, on the basis of probabilistic
arguments, and gave the distribution of velocities among the
molecules of a gas.
 Boltzmann is named after Ludwig Boltzmann who first
formulated it in 1868 during his studies of the statistical
mechanics of gases in thermal equilibrium.
Introduction:
The kinetic molecular theory is used to determine the motion of a molecule of an
ideal gas under a certain set of conditions. However, when looking at a mole of ideal
gas, it is impossible to measure the velocity of each molecule at every instant of time.
Therefore, the Maxwell-Boltzmann distribution is used to determine how many
molecules are moving between velocities v and v + dv. Assuming that the
one-dimensional distributions are independent of one another, that the velocity in
the y and z directions does not affect the x velocity, for example, the
Maxwell-Boltzmann distribution is given by

3. Equation:
𝑑𝑁
𝑁
=(
𝑚
2𝜋𝑘𝑏𝑇
)1/2 𝑑𝑣𝑒
−𝑚𝑣2
2𝜋𝑘𝑏𝑇
 dN/N is the fraction of molecules moving at velocity v to v + dv,
 m is the mass of the molecule,
 Kb is the Boltzmann constant, and
 T is the absolute temperature.
Equation in terms of function:
Additionally, the function can be written in terms of the scalar quantity
speed c instead of the vector quantity velocity. This form of the function defines
the distribution of the gas molecules moving at differentspeeds,
between c1 and c2, thus
f(c) = 4𝜋𝑐
2
(
𝑚
2𝜋𝑘𝑏𝑇
)
1/2 𝑑𝑣𝑒
−𝑚𝑣
2
2𝜋𝑘𝑏𝑇
Finally, the Maxwell-Boltzmann distribution can be used to determine the
distribution of the kinetic energy of for a set of molecules. The distribution of the
kinetic energy is identical to the distribution of the speeds fora certain gas at
any temperature.
Maxwell Boltzmann Distribution function
Graphs for different velocities of gases:
Following is a general graph in Maxwell Boltzmann representation used to plot for
showing how different gas molecules have different velocities. It shows molecules of gas at
y-axis and velocities at x-axis.

4. General Graph representation:
Graph No 1:
 The following graph shows the Maxwell-Boltzmann distribution of speeds for a
certain gas at a certain temperature, such as nitrogen at 298 K.
 The speed at the top of the curve is called the most probable speed because
the largest number of molecules have that speed.
Speed/velocities v
No of
molecules

5. Graph No 2:
 Graph 2 shows how the Maxwell-Boltzmann distribution is affected by
temperature. At lower temperatures, the molecules have less energy. Therefore,
the speeds of the molecules are lower and the distribution has a smaller range.
 As the temperature of the molecules increases, the distribution flattens out.
Because the molecules have greater energy at higher temperature, the
molecules are moving faster.
Graph No 3:

6.  Graph 3 shows the dependence of the Maxwell-Boltzmann distribution on
molecule mass.
 On average, heavier molecules move more slowly than lighter molecules.
Therefore, heavier molecules will have a smaller speed distribution, while
lighter molecules will have a speed distribution that is more spread out.
Speedexpressionderivation by Maxwell
Boltzmann distribution:
The root mean square speed expression, most probable speed and average speed
expression can be derived form the Maxwell Boltzmann distribution equation.
Root Square mean:
The root mean square expression is:
𝑉
𝑟𝑚𝑠 = √
3𝑅𝑇
𝑀
This root square mean quantity is interesting because the definition is hidden in the
name itself. The root-mean-square speed is the square root of the mean of
the squares of the velocities. Mean is just another word for average here.
Root-mean-square speed can also be written mathematically as:
𝑉𝑟𝑚𝑠 =√
1
𝑁
(𝑣2
1 + 𝑣3
2 + 𝑣4
3 +......)
Probable speed:
You might think that the speed located directly under the peak of the
Maxwell-Boltzmann graph is the average speed of a molecule in the gas, but that's

7. not true. The speed located directly under the peak is the Most probable speed.
Since it is the speed that is most likely to be found for a molecule in a gas.
Represented as follows:
𝑉
𝑚𝑝 = √
2𝑅𝑇
𝑀
Average speed:
The average speed Vavg of a molecule in the gas is :
𝑉
𝑎𝑣𝑔 = √
8𝑅𝑇
𝜋𝑀
Speeds shown in Maxwell Boltzmann distribution Graph:
Root mean square
speed line
Avg speed line
Probable
speed line

8. What does area under the Maxwell
Boltzmann Distributionshows?
The y-axis of the Maxwell-Boltzmann distribution graph gives the number of
molecules per unit speed. The total area under the entire curve is equal to the
total number of molecules in the gas.
If we heat the gas to a higher
temperature, the peak of the graph will shift to the right (since the average molecular
speed will increase). As the graph shifts to the right, the height of the graph has to
decrease in order to maintain the same total area under the curve. Similarly, as a
gas cools to a lower temperature, the peak of the graph shifts to the left. As the
graph shifts to the left, the height of the graph has to increase in order to maintain the
same area under the curve. This can be seen in the curves below which represent a
sample of gas (with a constant amount of molecules) at different temperatures.
As the gas gets colder, the graph becomes taller and more narrow. Similarly, as
the gas gets hotter the graph becomes shorter and wider. This is required for the area
under the curve (i.e. total number of molecules) to stay constant.
Cool Gas
Room temperature Gas
Hot Gas

9. If molecules enter the sample, the total area under the curve would increase.
Similarly, if molecules were to leave the sample, the total area under the curve would
decrease.