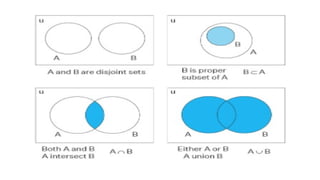
The document explains the concepts of sets, functions, and relations in mathematics, detailing four main set operations: union, intersection, complement, and difference. It defines a function as a relation where each input has a single output and discusses various types of relations such as empty, universal, identity, reflexive, symmetric, transitive, and equivalence relations. Additionally, it outlines operations on functions, including addition, subtraction, multiplication, division, and composition.

1. SETS, FUNCTION, RELATION

2. SET OPERATIONS
Set operations is a concept similar to fundamental operations on numbers.
Sets in math deal with a finite collection of objects, be it numbers, alphabets, or any
real-world objects.
Sometimes a necessity arises wherein we need to establish the relationship between
two or more sets.
There comes the concept of set operations.
There are four main set operations which include set union, set intersection, set
complement, and set difference.

3. THERE ARE FOUR MAIN KINDS OF SET
OPERATIONS WHICH ARE:
Union of sets
Intersection of sets
Complement of a set
Difference between sets/Relative Complement

4. UNION OF SETS
For two given sets A and B,
A B (read as A union B) is the set of distinct elements that belong to set A and B or
∪
both.
The number of elements in A B is given by
∪
n(A B) = n(A) + n(B) n(A B),
∪ − ∩
where n(X) is the number of elements in set X.
To understand this set operation of the union of sets better, let us consider an example:
If A = {1, 2, 3, 4} and B = {4, 5, 6, 7}, then the union of A and B is given by A B =
∪
{1, 2, 3, 4, 5, 6, 7}.

5. INTERSECTION OF SETS
For two given sets A and B, A B (read as A intersection B) is the set of common
∩
elements that belong to set A and B.
The number of elements in A B is given by
∩
n(A B) = n(A)+n(B) n(A B),
∩ − ∪
where n(X) is the number of elements in set X.
To understand this set operation of the intersection of sets better, let us consider an
example:
If A = {1, 2, 3, 4} and B = {3, 4, 5, 7}, then the intersection of A and B is given by A
B = {3, 4}.
∩

6. SET DIFFERENCE
The set operation difference between sets implies subtracting the elements from a set
which is similar to the concept of the difference between numbers.
The difference between sets A and B denoted as A B lists all the elements that are
−
in set A but not in set B.
To understand this set operation of set difference better, let us consider an example:
If
A = {1, 2, 3, 4} and B = {3, 4, 5, 7}, then the difference between sets A and B is
given by A - B = {1, 2}.

7. COMPLEMENT OF SETS
The complement of a set A denoted as A or A
′ c
(read as A complement) is defined as
the set of all the elements in the given universal set(U) that are not present in set A.
To understand this set operation of complement of sets better, let us consider an
example:
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9} and A = {1, 2, 3, 4}, then the complement of set A is
given by A' = {5, 6, 7, 8, 9}.

9. FUNCTION
A function is a relation in which every input is paired with exactly one
output. A function from set X to Y is the set of ordered pairs of real
numbers (x, y) in which no two distinct ordered pairs have the same first
component. Similar to a relation, the values of x are called the domain of
the function and the set of all resulting value of y is called the range or
co- domain of the function.

10. A function F from a set A to a set B is a relation with domain and co-
domain B that satisfies the following two properties:
1. For every element x in A, there is an element y in B such that (x, y) in F
2. For all elements x in A and y and z in B, If (x, y) in F and (x, z) in F then
y = z
These two properties; (1) and (2) can be stated less formally as follows:
1. Every element of A is the first element of an ordered pair of F. 2. No
two distinct ordered pairs in F have the same first element.

11. Is a function a relation? Focus on the x-coordinates, when given a relation.
• If the set of ordered pairs have different x-coordinates, it is a function.
• If the set of ordered pairs have same x-coordinates, it is NOT a function but it could
be said a relation.
Note: a) Y-coordinates have no bearing in determining functions
b) Function is a relation but relation could not be said as function.

12. Example1: Determine if the following is a function or not a function.
1. {(0, -5), (1, 4), (2, 3), (3, 2), (4, 1), (5, 0);
2. {(-1, -7), (1, 0), (2, 3), (0, -8), (0, 5), (-2, -1)}
3. 2x + 3y - 1 = 0
4. x ^ 2 + y ^ 2 = 1 5. y ^ 2 = x + 1

13. Example 2. Which of the following mapping represent a function?
1
2

14. Function Notations:
The symbol f(x) means function of x and it is read as "f of x." Thus, the
equation y = 2x + 1 could be written in a form of f(x) = 2x + 1 meaning y =
f(x) It can be stated that y is a function of x.
Let us say we have a function in a form of f(x) = 3x - 1 If we replace x 1,
this could be written as f(1) = 3(1) - 1 The notation f(1) only means that we
substitute the value of x = 1 resulting the function value. Thus (x) = 3x - 1
let x = 1 f(1) = 3(1) - 1 = 3 - 1 = 2 Another illustration is given a function g[x]
= x ^ 2 - 3 and let x = - 2 then g(- 2) = (- 2) ^ 2 - 3 = 1

15. Operations on Functions
The following are definitions on the operations on functions.
a. The sum or difference of f and g, denoted by f plus/minus g * i the
function defined by
(f plus/minus g)(x) = f(x) plus/minus g * (x) f(x) g(x). of f and g, denoted
by f g is the function defined by (fg)(x) =
c. The quotient of f and g denoted by f/g is the function defined by (f(x)) /
g * (x) where g(x) is not equal to zero.
d. The composite function of f and g denoted by fog is the function
defined by (f o g) (x) = f(g(x)) . Similarly, the composite function of g by f,
denoted by go f, is the defined by (g f) (x) = g(f(x)) .

16. Examples:
1. If f(x) = 2x + 1 and g(x) = 3x + 2 what is (f + g)(x) ?
Solution:
(f + g)(x) = f(x) + g(x)
= (2x + 1) + (3x + 2)
= 2x + 3x + 1 + 2
= 5x + 3
2. What is if f(x) = 2x + 1 and g(x) = 3x + 27 (fg)(x)
Solution:
(fg)(x) = f(x) * g(x) = (2x + 1)(3x + 2) = 6 * 2 + 7x + 2

17. 3. What is (f/g) (x) if f(x) = 2a + 6b and g(x) = a + 3b?
Solution:
(f / g)(x) = (f(x)) / g * (x) = (2a + 6b) / (a + 3b) = [2(a + 3b)] / a + 3b
4. If f(x) = 2x + 1 and g(x) = 3x + 2 what is (go f)(x)?
Solution:
(g f) (x) = g(f(x)) = g(2x + 1) = 3(2x + 1) + 2 = 6x + 3 + 2 = 6x + 5

18. RELATIONS
There are 8 main types of relations which include:
Empty Relation
Universal Relation
Identity Relation
Inverse Relation
Reflexive Relation
Symmetric Relation
Transitive Relation
Equivalence Relation

19. TYPES OF RELATIONS(CONT….)
Empty Relation
An empty relation (or void relation) is one in which there is no relation between any elements of a
set. For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x –
y| = 8. For empty relation,
R = A × A
φ ⊂
Universal Relation
A universal (or full relation) is a type of relation in which every element of a set is related to each
other. Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x –
y| ≥ 0. For universal relation,
R = A × A

20. TYPES OF RELATIONS(CONT….)
Identity Relation
In an identity relation, every element of a set is related to itself only. For example, in a
set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,
I = {(a, a), a A}
∈
Inverse Relation
Inverse relation is seen when a set has elements which are inverse pairs of another set.
For example if set A = {(a, b), (c, d)}, then inverse relation will be R-1
= {(b, a), (d, c)}.
So, for an inverse relation,
R-1
= {(b, a): (a, b) R}
∈

21. TYPES OF RELATIONS(CONT….)
Reflexive Relation
In a reflexive relation, every element maps to itself. For example, consider a set A = {1, 2,}. Now an
example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-
(a, a) R
∈
Symmetric Relation
In a symmetric relation, if a=b is true then b=a is also true. In other words, a relation R is symmetric
only if (b, a) R is true when (a,b) R. An example of symmetric relation will be R = {(1, 2), (2, 1)}
∈ ∈
for a set A = {1, 2}. So, for a symmetric relation,
aRb bRa, a, b A
⇒ ∀ ∈
.

22. TYPES OF RELATIONS(CONT….)
Transitive Relation
For transitive relation, if (x, y) R, (y, z) R, then (x, z) R. For a transitive
∈ ∈ ∈
relation,
aRb and bRc aRc a, b, c A
⇒ ∀ ∈
Equivalence Relation
If a relation is reflexive, symmetric and transitive at the same time it is known as an
equivalence relation

23. PARTIALLY ORDERING
Partial Order Relations
A relation R on a set A is called a partial order relation if it satisfies the following
three properties:
Relation R is Reflexive, i.e. aRa a A.
∀ ∈
Relation R is Antisymmetric, i.e., aRb and bRa a = b.
⟹
Relation R is transitive, i.e., aRb and bRc aRc.
⟹

24. THANK YOU