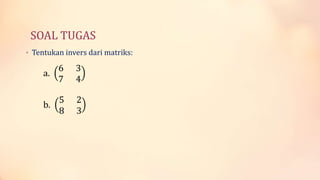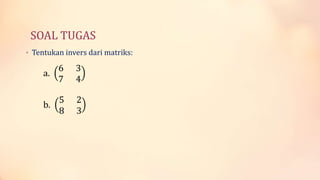
Dokumen ini membahas cara menghitung invers matriks 2x2, termasuk rumus determinan dan situasi di mana matriks tidak memiliki invers. Contoh soal dan langkah-langkah penyelesaian diuraikan untuk menunjukkan proses perhitungan. Selain itu, terdapat tugas untuk menemukan invers dari beberapa matriks lain.

1. INVERS MATRIKS
Jumat, 21 APRIL 2020

2. Invers Matriks (2 x 2)
Jika A =
maka invers matriks A
• ad – bc merupakan rumus dari determinan matriks A atau
det (A) atau 𝐴
• Jika ad – bc = 0  matriks tidak mempunyai invers
(matriks singular) atau jika determinan matriks A bernilai
0 maka matriks tersebut tidak mempunyai invers.






dc
ba









ac
bd11
bc-ad
A

3. Contoh Soal:
• invers matriks A =






35
12









25
13
5-6
1









25
13
1.5-2.3
1
A 1









25
13









ac
bd
bc-ad
1
A 1

4. Contoh Soal

5. Solusi
• Untuk menemukan matriks invers 2×2 yang
berdekatan, kita hanya perlu menukar atau
memindahkan elemen yang posisinya ada di baris
pertama kolom pertama dengan elemen-elemen di
baris kedua kolom kedua.
• Berikutnya, baris kedua dari kolom pertama dan baris
pertama dari kolom kedua dikalikan dengan -1.
Hasilnya adalah sebagai berikut.
Selanjutnya, cari determinan matriks
det A = (2 × 6) – (4 × 1)
= 12 – 4
= 8
Selanjutnya, kita masukkan ke dalam
rumus
𝐴−1
=
3
4
−
1
8
−
1
2
1
4
𝐴−1
=
1
8
𝑥 6
1
8
𝑥 (−1)
1
8
𝑥 (−4)
1
8
𝑥 2
𝐴−1
=
1
8
𝑥
6 − 1
−4 2
𝐴−1 =
1
det(𝐴)
𝑥 𝐴𝑑𝑗 (𝐴)

6. SOAL TUGAS
• Tentukan invers dari matriks:
a.
6 3
7 4
b.
5 2
8 3

7. TERIMAKASIH