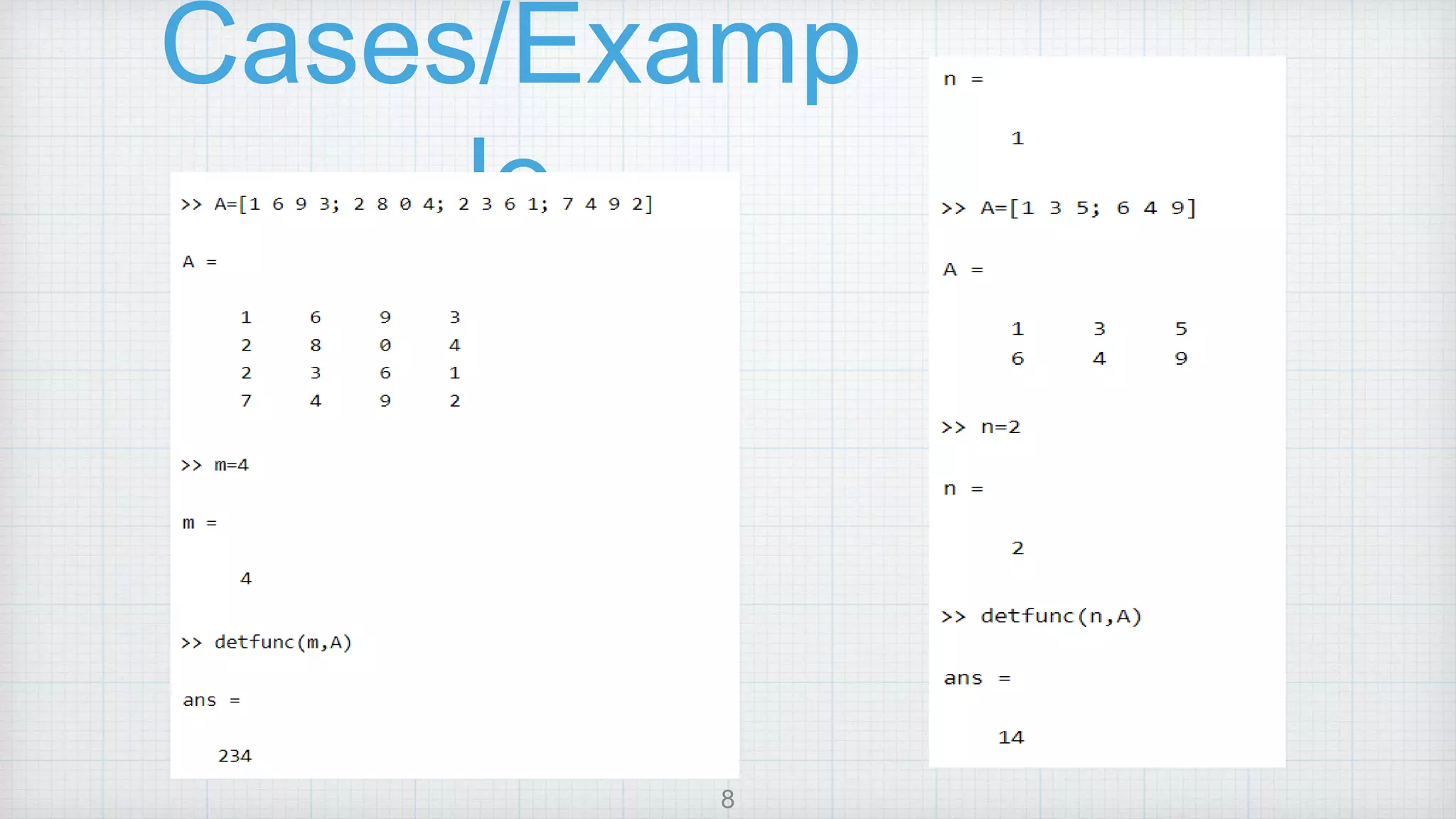
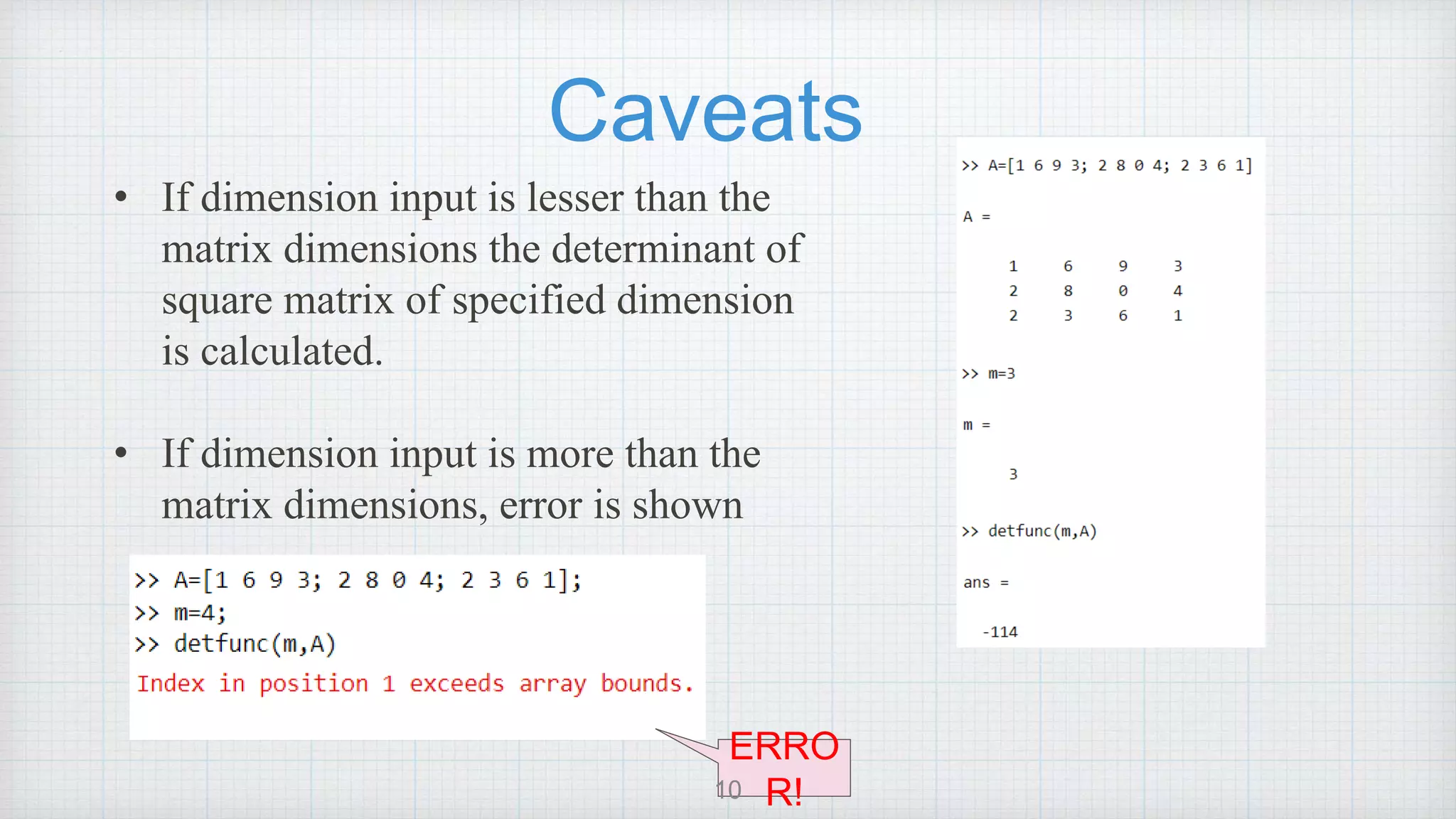
This document describes a MATLAB script and function to calculate the determinant of a matrix without using the built-in det() function. It explains: 1) Converting the script into a function file that accepts the matrix and its dimension as inputs and returns the determinant. 2) The methodology uses cofactor expansion and calls the function recursively to compute the determinant. 3) The time complexity of the function is O(n!) due to the nested for loops and recursive calls.

1. PRACTICAL
Name- Saloni Singhal
M.Sc. (Statistics) II-Sem.
Roll No: 2046398
Course- MATH-409 L
Numerical Analysis Lab
Submitted To: Dr. S.C. Pandey
1

2. OBJECTIVE
• To write Script and functions in MATLAB (M-files)
• Converting script files into function files for a given
program and vice-versa
Problem Statement
To find the determinant of an arbitrarily sized matrix entered
by the user without using the det() built-in function.
Methodology:
Using co-factor expansion of the determinant definition and,
calling functions recursively to compute the same.
2

3. Theory
Script files are the simplest type of
MATLAB program that contains multiple
sequential lines of MATLAB commands
and function calls.
To create a script, use the edit command or
open using the New tab.
They simply work by pressing Run as it
has taken input. They are saved with (.m)
extension
Function files are program routines,
implemented in M-files, they accept input
arguments and return output arguments.
Syntax:
They operate on variables within their
own workspace. This workspace is
separate from the workspace accessed at
the MATLAB command prompt.
Script File Function File
3

4. Determinants
4
• The determinant (in linear algebra) is a value associated with a
square matrix, that is a matrix with as many rows as columns.
• Determinant of a matrix A is given by det(A). determinant is a real
number, it is not a matrix.
• determinant only exists for square matrices
Cofactor expansion: determinant is obtained by
multiplying the entries in any row/column of A
by the corresponding cofactors and adding the
resulting products
det(A) = a1jC1j + a2jC2j + ... + anjCnj
det(A) = ai1Ci1 + ai2Ci2 + ... + ainCin1
To map between two distinct vector
spaces, we define a volume on each
of them. Then the “determinant” of a
linear map between them would be
the (inverse) ratio between the
volume of a parallelepiped in the
domain and the volume of its image.
Any nonzero multiple of a volume
form is again a volume form. So the
ambiguity resulting from these
arbitrary scale factors renders that
“determinant” useless.

5. Script File
m=input("define matrix dimension");
fprintf("%dn",m)
A=input("enter matrix of dimension m");
A
d=determinant(m,A)
%{ determinant expansion
det(M)=sum{i=1:n}((-1)^i * a(1,i) * det(M(1,i))
%}
function detm = determinant(n,M)
detm = 0; %dimension is unity
if n==1
detm = M(1,1)
5

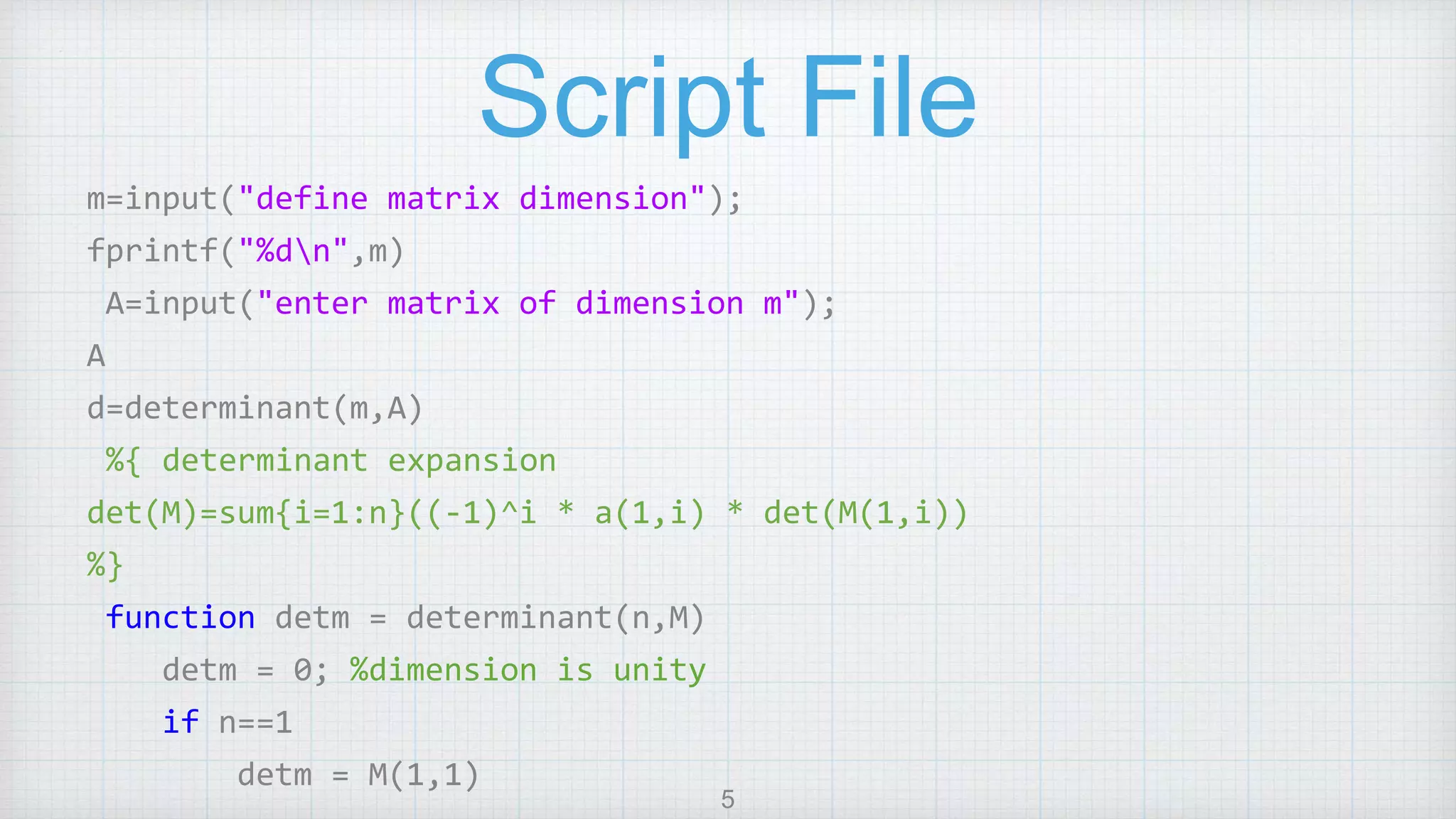
6. Program Contd.
else
for i=1:n
M1 = M
M1(1,:)=[]
M1(:,i)=[]
detm = detm + ((-1)^i)*M(1,i)*determinant(n-1,M1)
end
end
end
Outputs
Verification
6

7. Function File
function detm = detfunc(n,M)
detm = 0;
if n==1
detm = M(1,1);
else
for i=1:n
M1 = M;
M1(1,:)=[];
M1(:,i)=[];
detm = detm + ((-1)^i)*M(1,i)*detfunc(n-1,M1);
end
end
end 7

8. Cases/Examp
le
8

9. Time Complexity
9
For the given program it is calculated as:
T(n)=n*(4+T(n-1))
T(n-1)=(n-1)*(4+T(n-2))
T(n)= n*(4+(n-1)*(4+(n-2)*(4+…))
T(n)=4n+4n(n-1)+4n(n-1)+4n(n-1)(n-2)…..1
T(n)=O(n!)
Big O notation is the most common metric for calculating time complexity. It
describes the execution time of a task in relation to the number of steps
required to complete it.
Initially for if loop
of range 1:n, we
take n operations,
then 4 operation
inside the loop
followed by a
recursive function.
‘O’ takes its
dominant value

10. Caveats
• If dimension input is lesser than the
matrix dimensions the determinant of
square matrix of specified dimension
is calculated.
• If dimension input is more than the
matrix dimensions, error is shown
ERRO
R!
10

11. Conclusion
• MATLAB allows writing two kinds of program files. We can use the
MATLAB editor or any other text editor to create m-files.
• Function can be used within same script (locally)
• Function file can be used anywhere globally even in a script file as shown
below.
11
References
• MATLAB help
• https://mathinsight.org/determina
nt_matrix