This document discusses the importance and advantages of MATLAB. It notes that MATLAB has matrices as its basic data element, supports vectorized operations, and has built-in graphical and statistical functions. Toolboxes can further expand MATLAB's functionality. While it uses more memory and CPU time than other languages, MATLAB allows both command line and programming capabilities. The document provides examples of how to create matrices, perform operations on matrices using functions like sum(), transpose(), and indexing. It also discusses matrix multiplication and how operations depend on matrix dimensions.

1. IMPORTANCE OF
MATLAB
By,
K. Rajesh,
Assistant Professor,
Department of ECE,
SSMIET

2. Why should we use MATLAB (Matrix Laboratory)?

3. MATLAB has several advantages over other methods
or languages:
• Its basic data element is the matrix. A simple integer is considered an
matrix of one row and one column. Several mathematical operations
that work on arrays or matrices are built-in to the Mat lab environment.
For example, cross-products, dot-products, determinants, inverse
matrices.
• Vectorized operations. Adding two arrays together needs only one
command, instead of a for or while loop.
• The graphical output is optimized for interaction. You can plot your
data very easily, and then change colors, sizes, scales, etc, by using the
graphical interactive tools.
• Mat lab's functionality can be greatly expanded by the addition of
toolboxes. These are sets of specific functions that provided more
specialized functionality. Ex: Excel link allows data to be written in a
format recognized by Excel, Statistics Toolbox allows more specialized
statistical manipulation of data (Anova, Basic Fits, etc)

4. There are also disadvantages:
• It uses a large amount of memory and on slow
computers it is very hard to use.
• It sits “on top” of Windows, getting as much
CPU time as Windows allows it to have. This
makes real-time applications very complicated.

5. USING MATLAB
 Matlab in not only a programming language, but a programming
environment as well.
 You can perform operations from the command line, as a sophisticated
calculator.
 Or you can create programs and functions that perform repetitive tasks,
just as any other computer language.
Try a simple operation now:
2 + 2 <enter>
Answer is ‘4’ displayed immediately on
command window

6. One of the most important features of the
MATLAB interface is the help. It is very
thorough and you can learn almost anything you
need from it.
Help <enter>

7. Let’s start doing something interesting with
MATLAB

8. The best way for you to get started with MATLAB is to
learn how to handle matrices !!!!!
You can enter matrices into MATLAB in several
different ways:
1. Enter an explicit list of elements.
2. Load matrices from external data files.
3. Generate matrices using built-in functions.
4. Create matrices with your own functions in M-
files.

9. How to create Matrices?
1. Separate the elements of a row with blanks or commas.
2. Use a semicolon, ; , to indicate the end of each row.
3. Surround the entire list of elements with square brackets, [ ]
A = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1]
This is what MATLAB displays after you hit <enter>
A =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
MAGIC SQUARE
BACK

10. Let’s prove it is a magic square. Let’s get the sum
of all columns by typing ’sum(A)’
The answer (ans) is:
ans =
34 34 34 34
This result is a row vector. Each column in A adds
up to 34. That’s magic!

11. How about the row sums? MATLAB has a preference for working with the
columns of a matrix, so the easiest way to get the row sums is to transpose
the matrix, compute the column sums of the transpose, and then transpose
the result. The transpose operation is denoted by an apostrophe or single
quote, '. It flips a matrix about its main diagonal and it turns a row vector
into a column vector.
A'
ans =
16 5 9 4
3 10 6 15
2 11 7 14
13 8 12 1
Now: sum(A')' produces a column vector containing the row sums
ans =
34
34
34
34

12. Notice the double ‘. This is a very important
concept to develop when using Matlab.
A’ is the transpose of A. “ sum(A’) “ looks the
same as “ sum(A) “, but the first is a sum of the
rows of A, the second the sum of columns of A.
So, the double ‘ , makes the result reflect its
original configuration.

13. The sum of the elements on the main diagonal is easily obtained
with the help of the ‘diag’ function, which picks off that
diagonal.
diag(A)
ans =
16
10
7
1
sum(diag(A))
ans =
34

14. Another good example to illustrate the use of ‘
B = [1 1 1; 2 2 2; 3 3 3]
B =
1 1 1
2 2 2
3 3 3
sum(B)
ans =
6 6 6
sum(B')
ans =
3 6 9
sum(B')'
ans =
3
6
9
B'
ans =
1 2 3
1 2 3
1 2 3

15. The element in row i and column j of A is denoted by A(i,j).
For example, A(4,2) is the number in the fourth row and
second column. For our magic square, A(4,2) is 15. So it
is possible to compute the sum of the elements in the
fourth column of A by typing
A(1,4) + A(2,4) + A(3,4) + A(4,4)
ans =
34
The most effective way to perform this operation is using
the ‘:’ operator, one of Matlab’s workhorses :
sum(A(:,4))
ans =
34
It reads as “add every element in column 4”

16. If you want to see these elements, simply type
A(:,4)
ans =
13
8
12
1
This operation preserves the original format of the
data. Column 4 looks like a column

17. We can also refer to the elements of a matrix with a
single subscript, A(k). This is the usual way of
referencing row and column vectors. But it can also
apply to a fully two-dimensional matrix, in which
case the array is regarded as one long column vector
formed from the columns of the original matrix. So,
for our magic square, A(8) is another way of
referring to the value 15 stored in A(4,2).
A =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1

18. Question No: 01
t = A(4,5)
Is this correct ?
If not why?

19. Answer: 01
t = A(4,5)
This is wrong…..
Because …..
This happens because A has only 4 columns and 4
rows. A(4,5) is undefined. Verify this by
typing size(A)
ans =
4 4

20. However, you can store a value in an element outside of
the matrix, and the size increases to accommodate it
X = A;
X(4,5) = 17
X =
16 3 2 13 0
5 10 11 8 0
9 6 7 12 0
4 15 14 1 17
Now verify that size(X)
ans =
4 5

21. MORE ON ‘:’
Question No: 02
>>1:10

22. MORE ON ‘:’
Answer No: 02
>>1:10
ans =
1 2 3 4 5 6 7 8 9 10
creates a row vector containing the integers from 1
to 10.

23. You can also use real or negative steps between
numbers:
100 : -7 : 50
100 93 86 79 72 65 58 51
0:pi/4:pi
0 0.7854 1.5708 2.3562 3.1416

24. Creating Matrices
Although MATLAB does not required formal memory allocation, it is a
good idea to do so when working with matrices. MATLAB tends to
respect the format in the following declarations: zeros is used to create
a matrix of all zeros
Z = zeros(2,4)
Z = 0 0 0 0 0 0 0 0
ones is used to create a matrix of all ones
F = 5*ones(3,3)
F = 5 5 5
5 5 5
5 5 5

25. ‘rand‘ generates random numbers
Ex:
X=rand(4,4);
X =
0.9049 0.2581 0.6028 0.2967
0.9797 0.4087 0.7112 0.3188
0.4389 0.5949 0.2217 0.4242
0.1111 0.2622 0.1174 0.5079
X=
0.0855 0.9289 0.2373 0.5211
0.2625 0.7303 0.4588 0.2316
0.8010 0.4886 0.9631 0.4889
0.0292 0.5785 0.5468 0.6241
Look at the two
different answers
when we use rand
function two times
consecutively

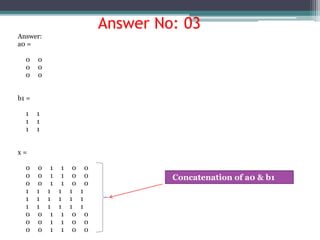
26. Question No: 03
What is the answer?
a0 = zeros(3, 2);
b1 = ones(3, 2);
x = [a0, b1, a0; b1, b1, b1; a0, b1, a0];

27. Answer No: 03
Answer:
a0 =
0 0
0 0
0 0
b1 =
1 1
1 1
1 1
x =
0 0 1 1 0 0
0 0 1 1 0 0
0 0 1 1 0 0
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
0 0 1 1 0 0
0 0 1 1 0 0
0 0 1 1 0 0
Concatenation of a0 & b1

28. Question No: 04
f = ones(2,3) * 2
g = ones(3,2) * 3
Will f × g is equal to g × f ?

29. Answer No: 04
f = ones(2,3) * 2
g = ones(3,2) * 3
f =
2 2 2
2 2 2
g =
3 3
3 3
3 3
>> f*g
ans =
18 18
18 18
>> g*f
ans =
12 12 12
12 12 12
12 12 12
So, f × g is not equal to g × f

30. Not ended here… more to go…