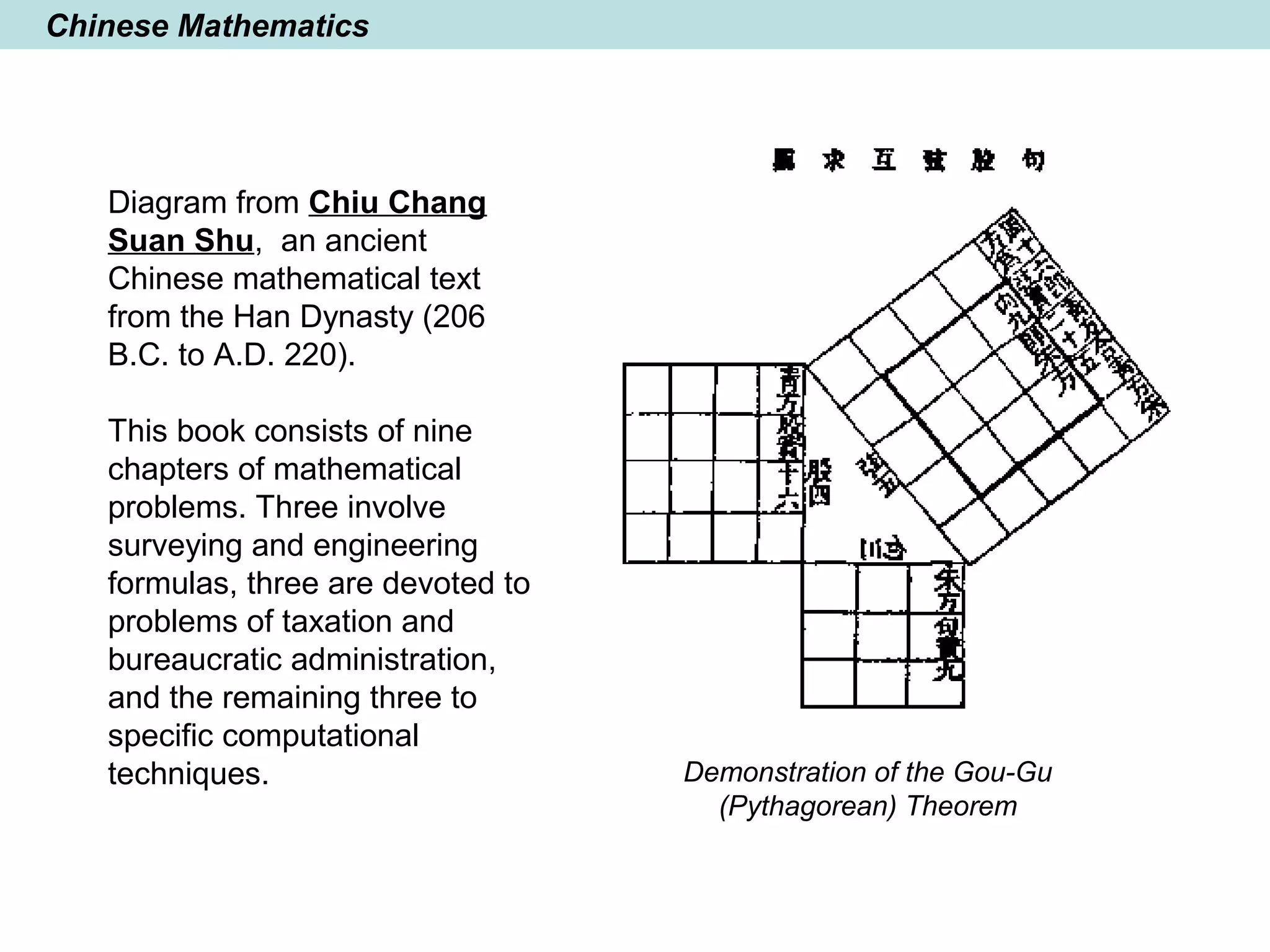
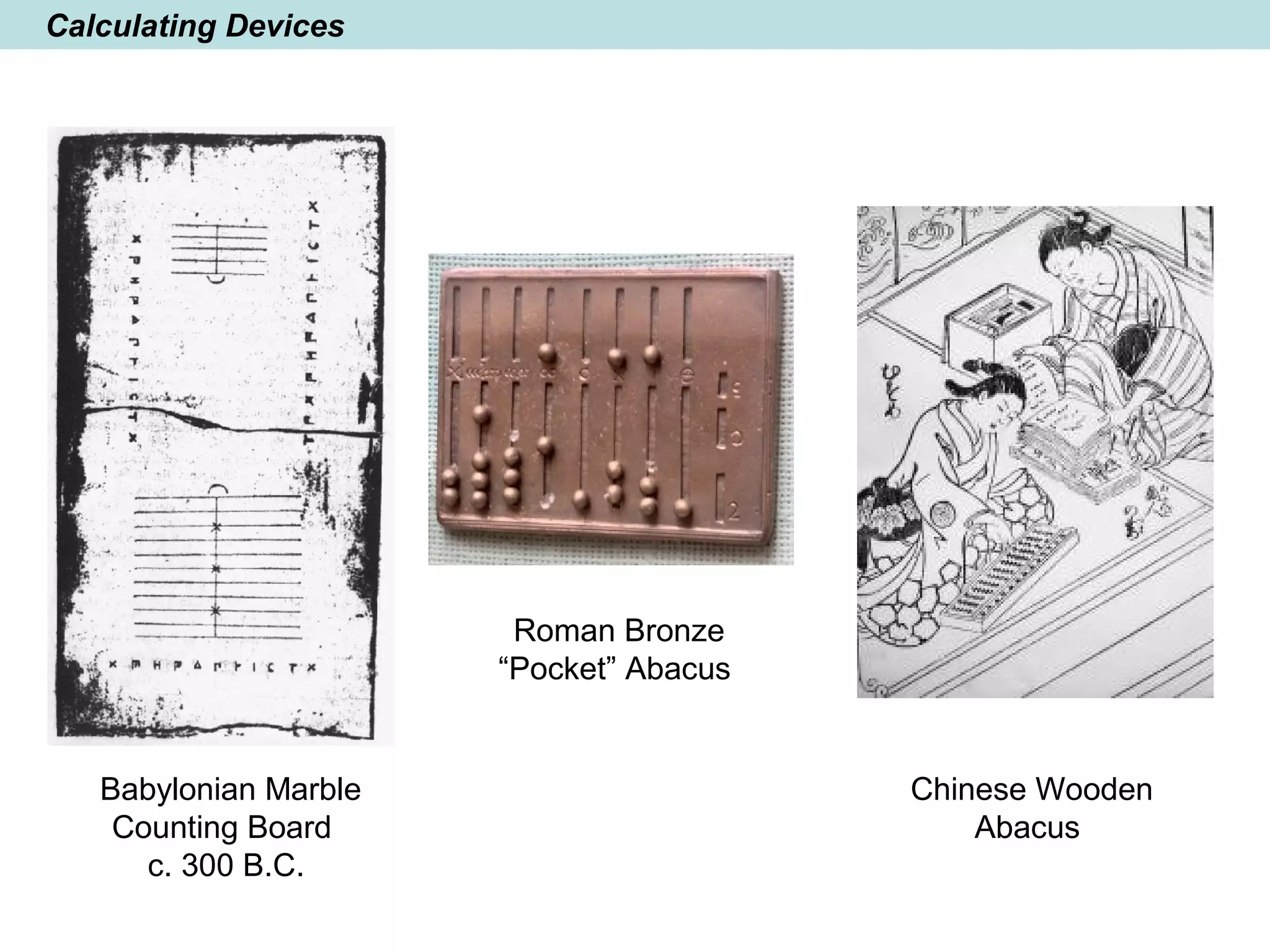
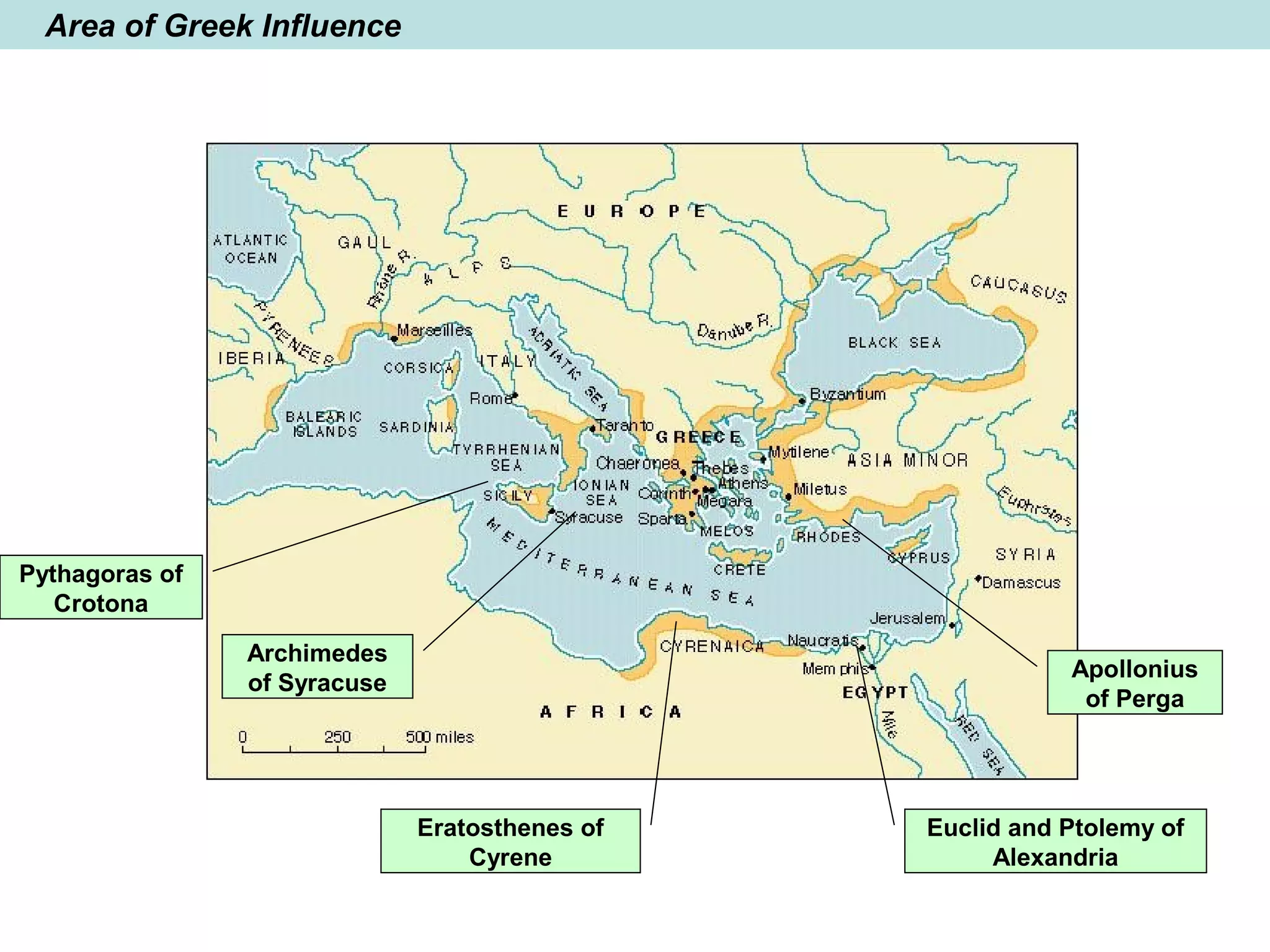
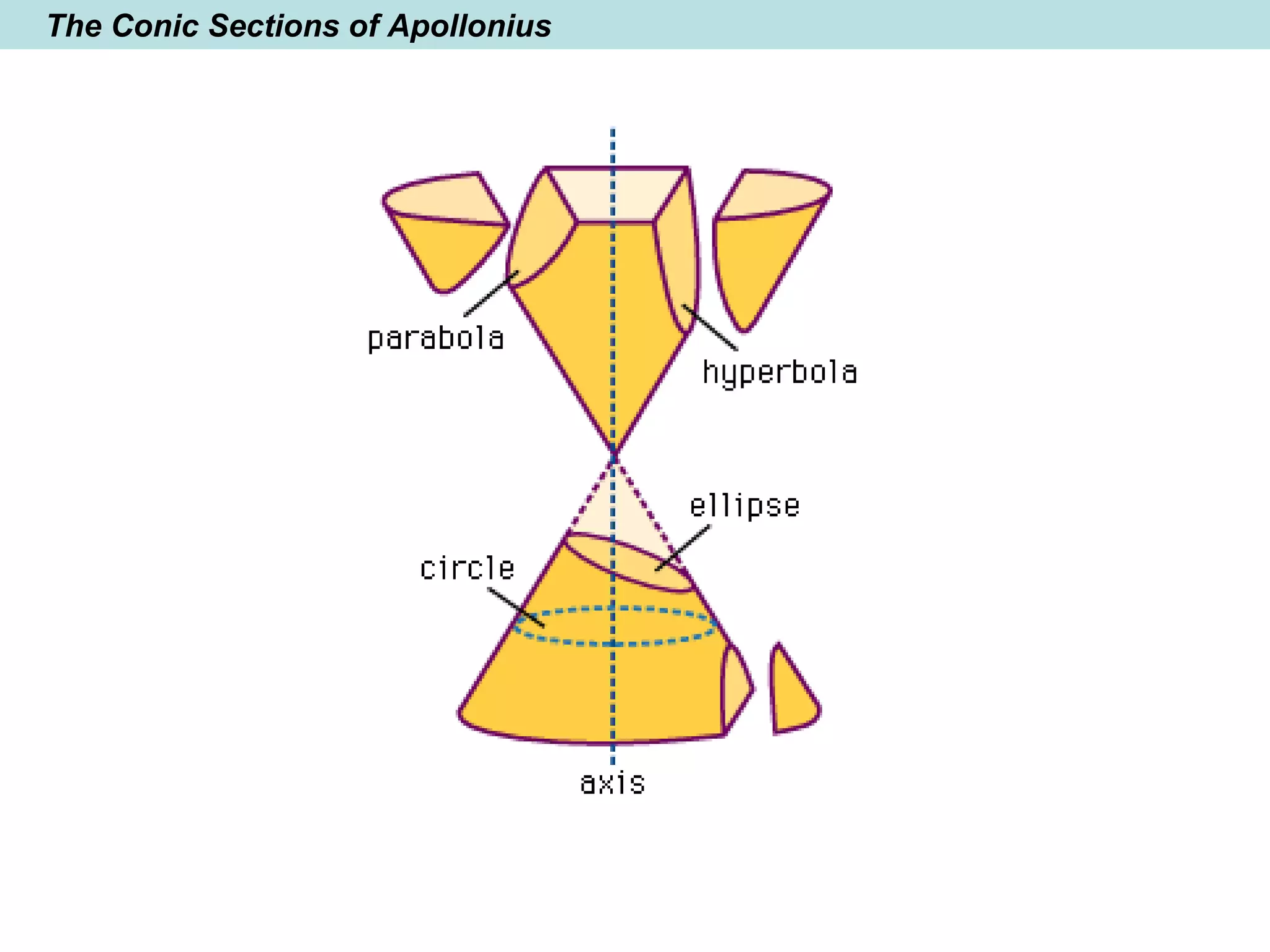
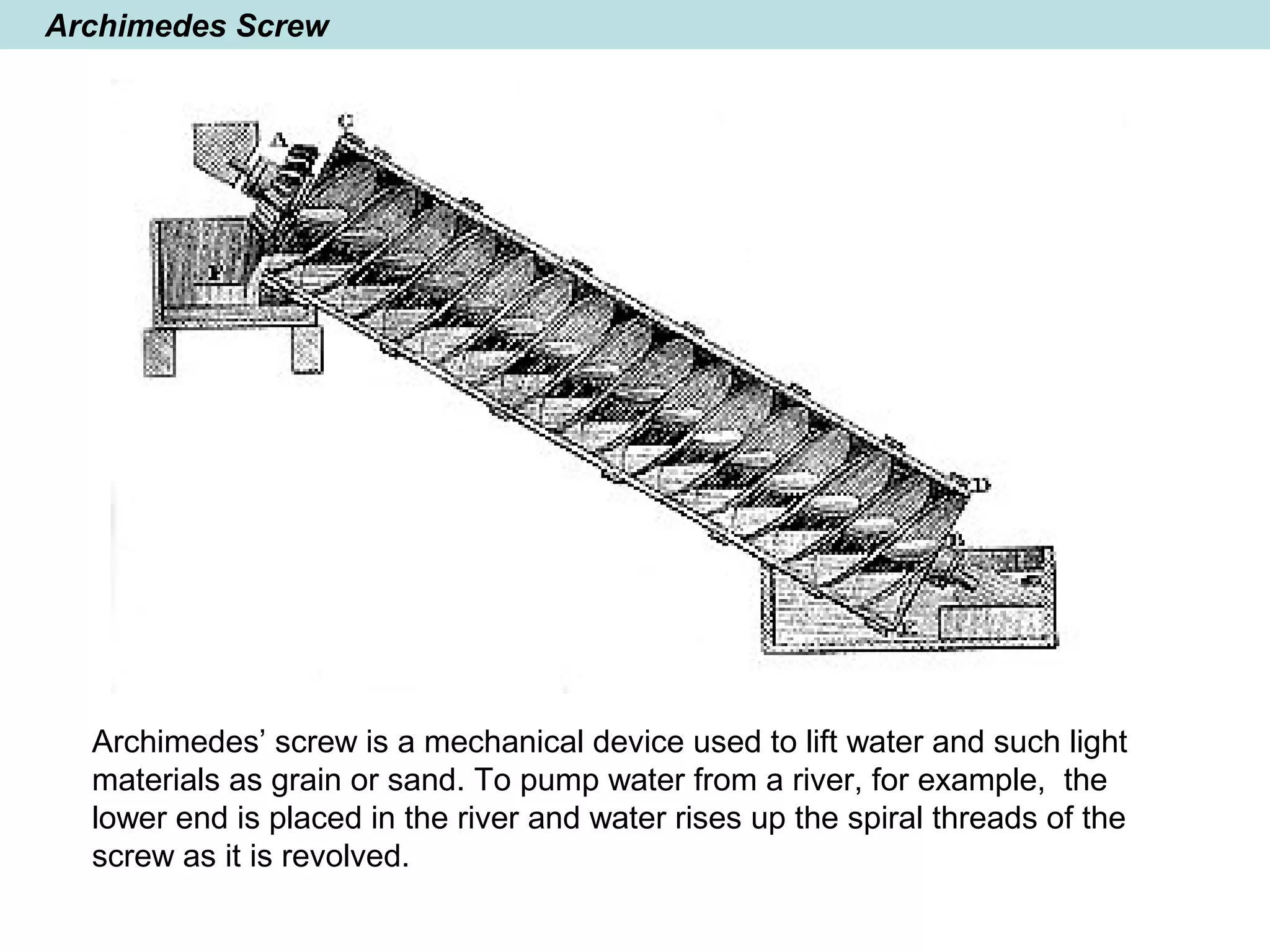
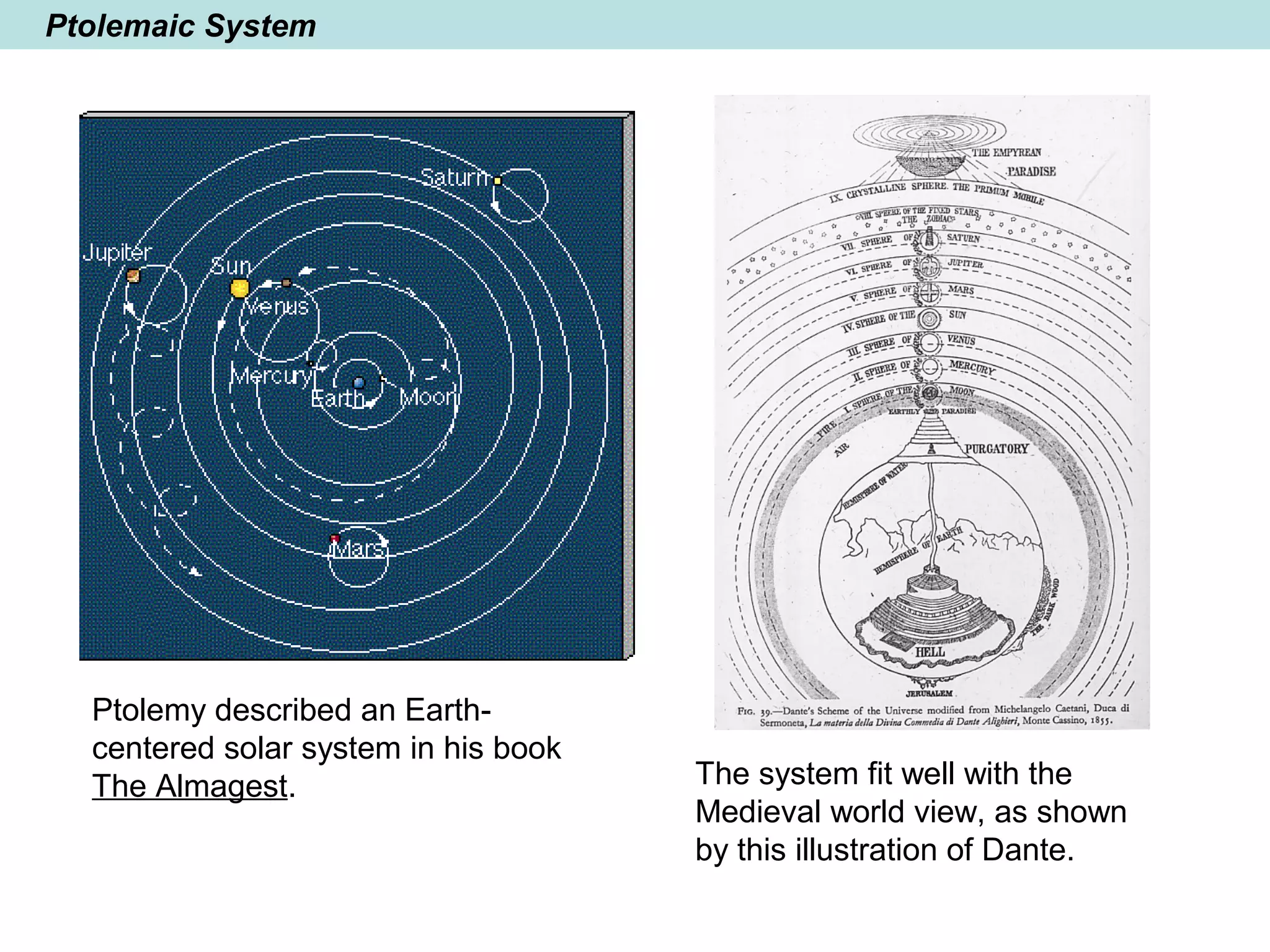
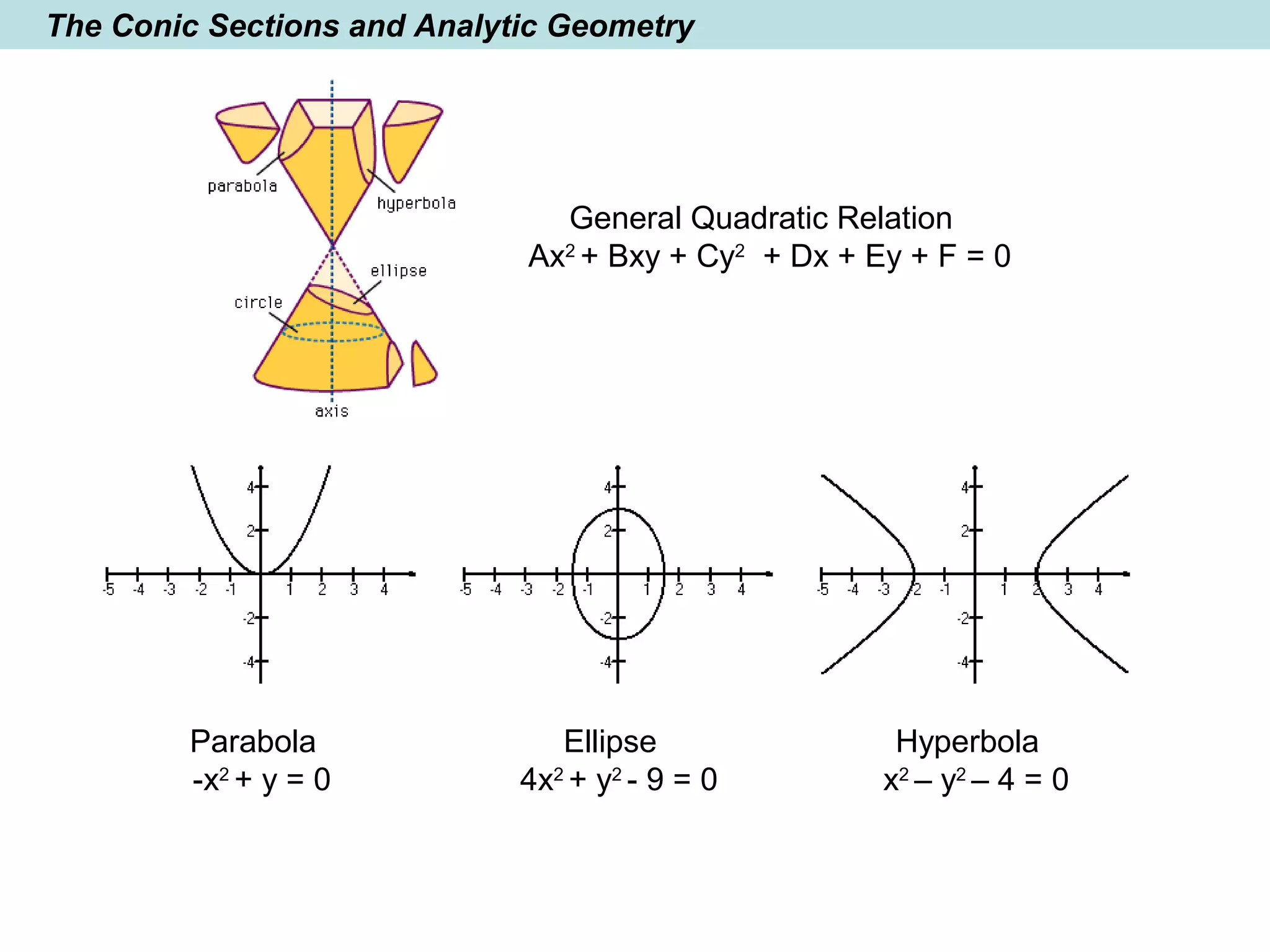
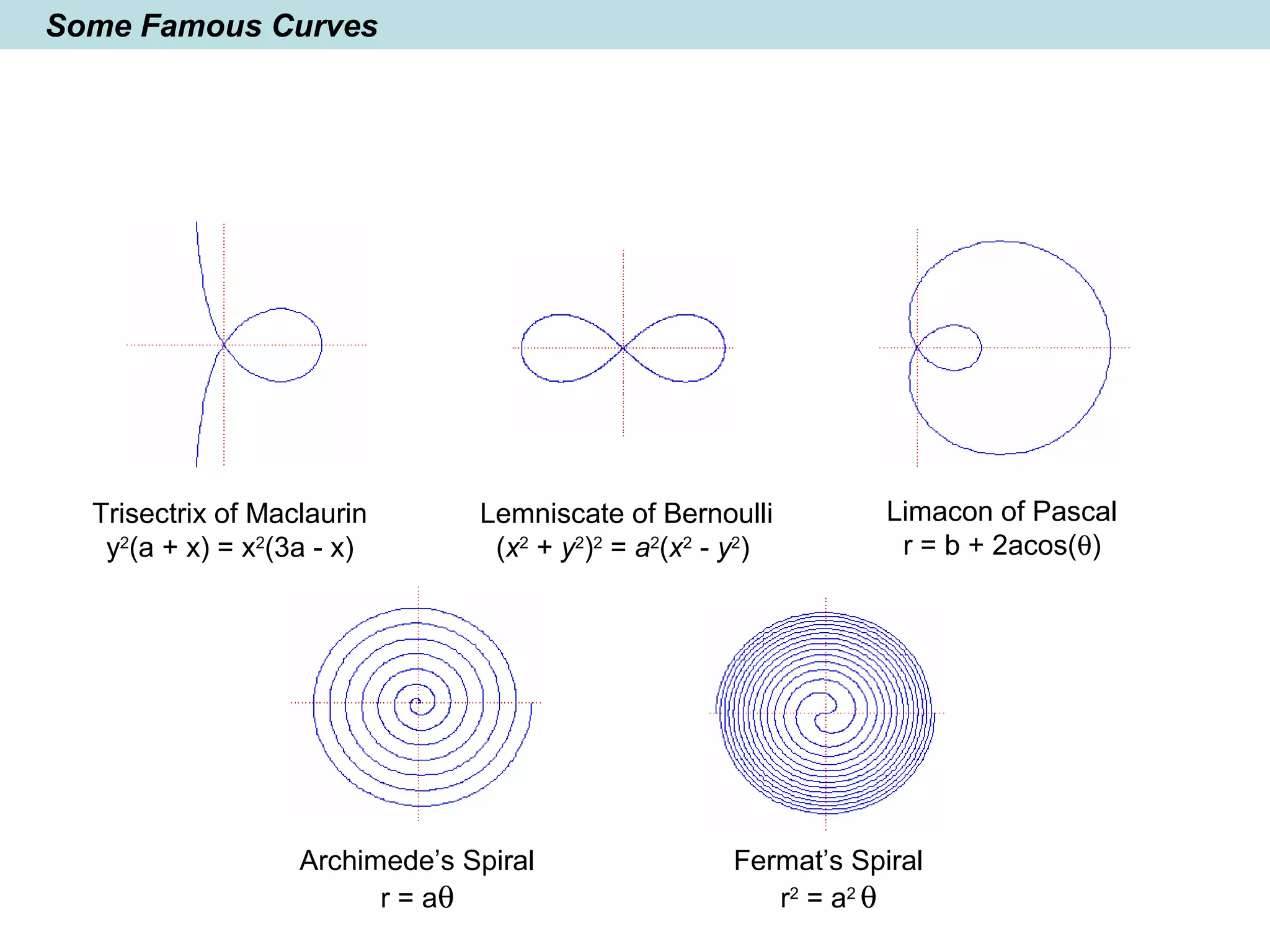
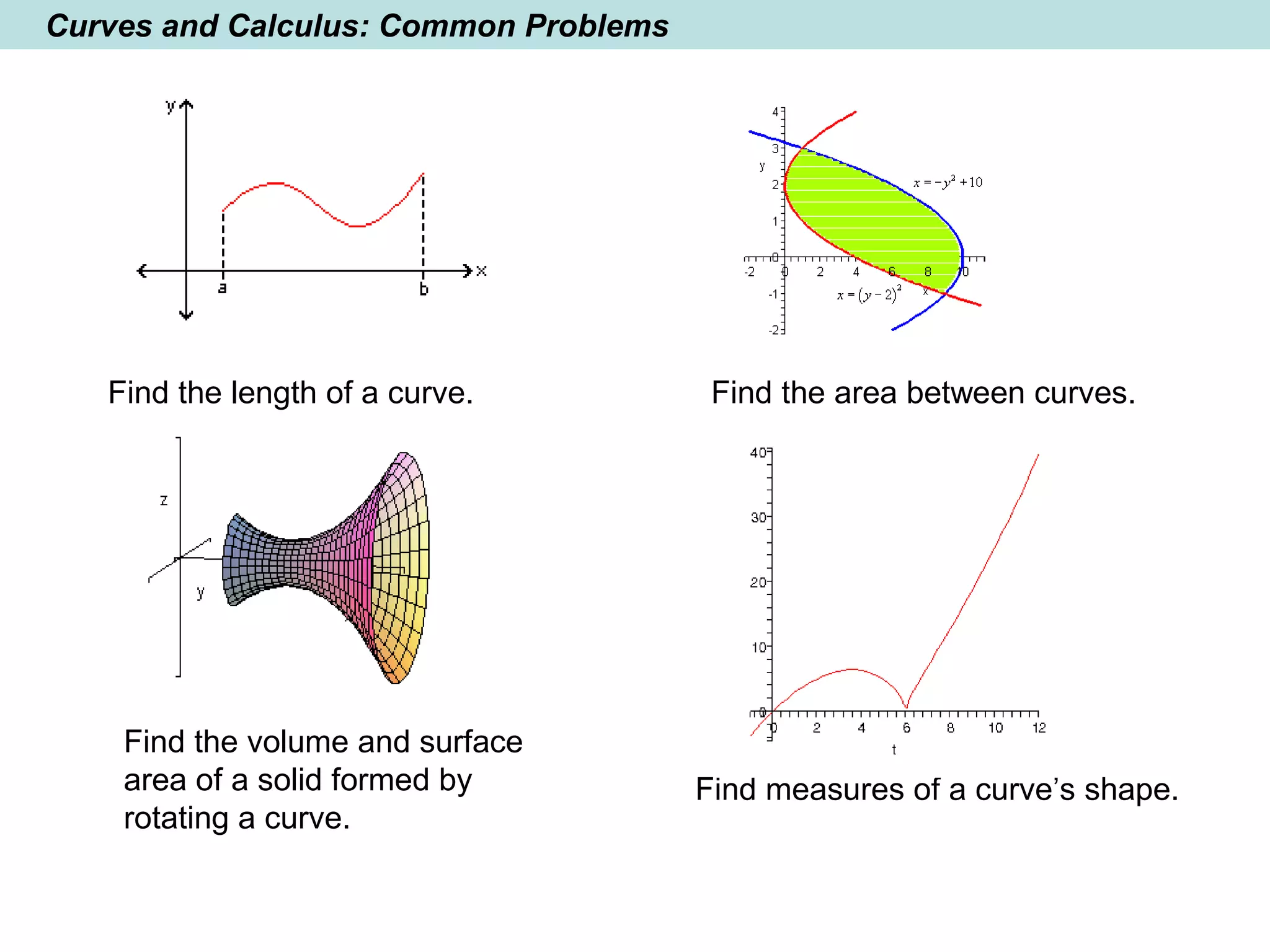
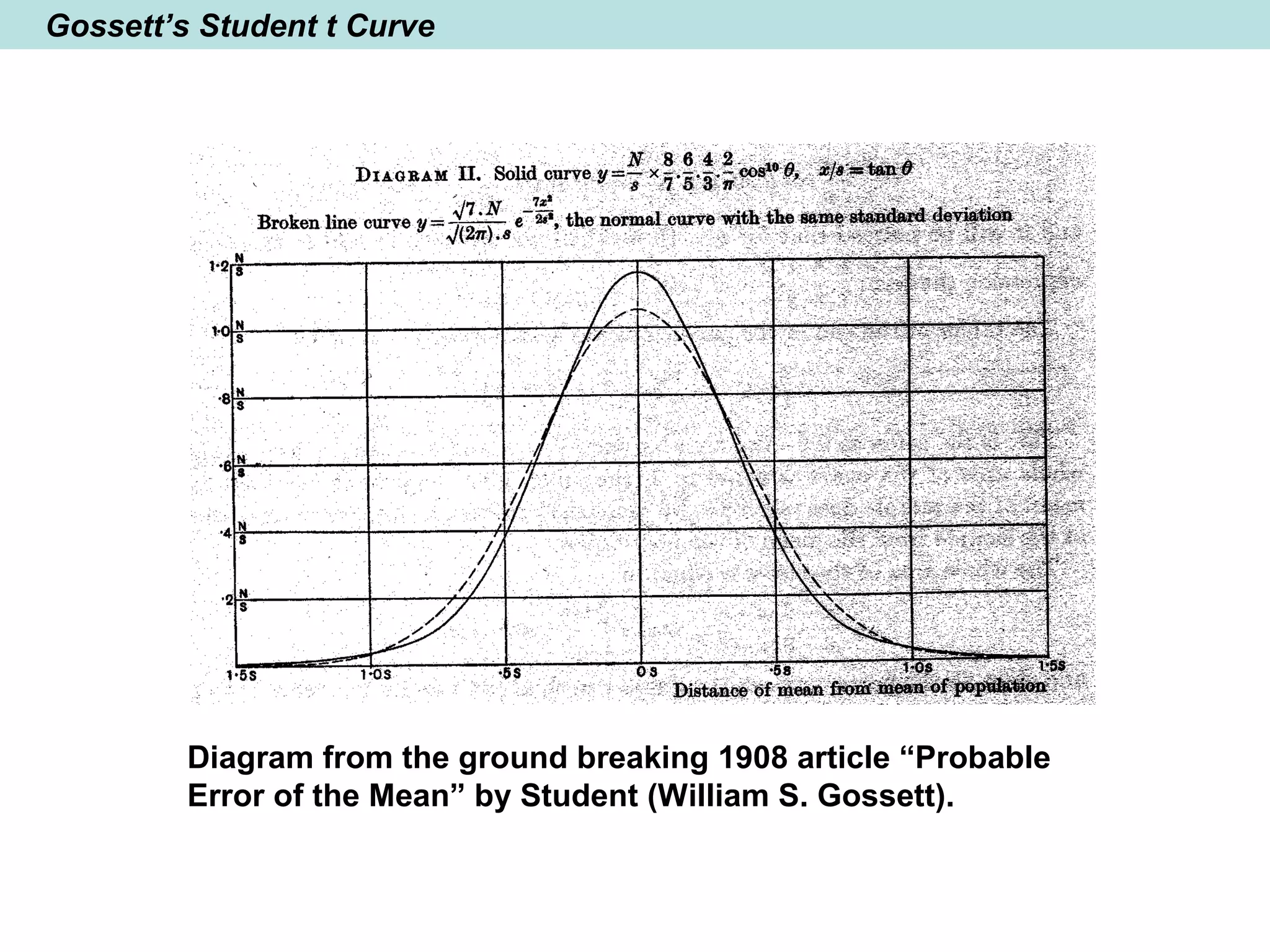
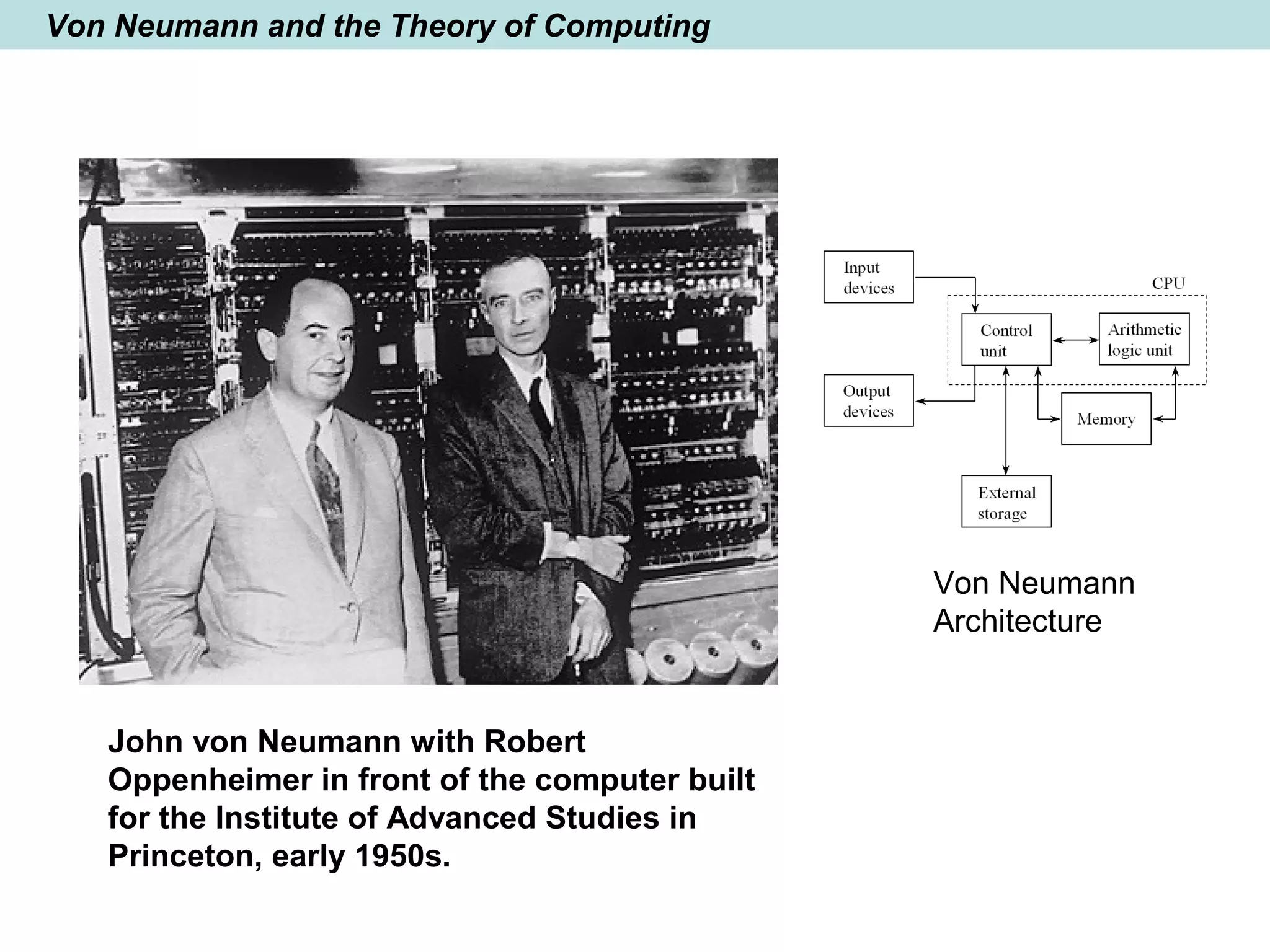
The document provides a brief history of mathematics from ancient to modern periods. It covers the development of numeration systems and arithmetic, geometry, algebra, trigonometry, calculus, and analytic geometry. Key developments include ancient civilizations developing practical math for trade and construction, Greeks establishing logic-based math and Euclidean geometry, Hindus and Arabs advancing the decimal numeral system and algebra, and Europeans in the early modern period making advances in trigonometry, logarithms, analytic geometry, and calculus.

1. A Brief History of Mathematics
• Ancient Period
• Greek Period
• Hindu-Arabic Period
• Period of Transmission
• Early Modern Period
• Modern Period

2. A. Number Systems and Arithmetic
• Development of numeration systems.
• Creation of arithmetic techniques, lookup tables, the abacus and other
calculation tools.
B. Practical Measurement, Geometry and Astronomy
• Measurement units devised to quantify distance, area, volume, and
time.
• Geometric reasoning used to measure distances indirectly.
• Calendars invented to predict seasons, astronomical events.
• Geometrical forms and patterns appear in art and architecture.
Ancient Period (3000 B.C. to 260 A.D.)

3. Practical Mathematics
As ancient civilizations developed, the
need for practical mathematics
increased. They required numeration
systems and arithmetic techniques for
trade, measurement strategies for
construction, and astronomical
calculations to track the seasons and
cosmic cycles.

4. Babylonian Numerals
The Babylonian Tablet Plimpton 322
This mathematical tablet was recovered from an unknown place in the Iraqi
desert. It was written originally sometime around 1800 BC. The tablet
presents a list of Pythagorean triples written in Babylonian numerals. This
numeration system uses only two symbols and a base of sixty.

5. Chinese Mathematics
Diagram from Chiu Chang
Suan Shu, an ancient
Chinese mathematical text
from the Han Dynasty (206
B.C. to A.D. 220).
This book consists of nine
chapters of mathematical
problems. Three involve
surveying and engineering
formulas, three are devoted to
problems of taxation and
bureaucratic administration,
and the remaining three to
specific computational
techniques. Demonstration of the Gou-Gu
(Pythagorean) Theorem

6. Calculating Devices
Chinese Wooden
Abacus
Roman Bronze
“Pocket” Abacus
Babylonian Marble
Counting Board
c. 300 B.C.

7. A. Greek Logic and Philosophy
• Greek philosophers promote logical, rational explanations of natural
phenomena.
• Schools of logic, science and mathematics are established.
• Mathematics is viewed as more than a tool to solve practical problems;
it is seen as a means to understand divine laws.
• Mathematicians achieve fame, are valued for their work.
B. Euclidean Geometry
• The first mathematical system based on postulates, theorems and
proofs appears in Euclid's Elements.
Greek Period (600 B.C. to 450 A.D.)

8. Area of Greek Influence
Archimedes
of Syracuse
Euclid and Ptolemy of
Alexandria
Pythagoras of
Crotona
Apollonius
of Perga
Eratosthenes of
Cyrene

9. Mathematics and Greek Philosophy
Greek philosophers viewed the universe in mathematical terms. Plato
described five elements that form the world and related them to the five
regular polyhedra.

10. Euclid’s Elements
Greek, c. 800 Arabic, c. 1250 Latin, c. 1120
French, c. 1564 English, c. 1570 Chinese, c. 1607
Translations of Euclid’s Elements of Gemetry
Proposition 47, the Pythagorean Theorem

11. The Conic Sections of Apollonius

12. Archimedes and the Crown
Eureka!

13. Archimedes Screw
Archimedes’ screw is a mechanical device used to lift water and such light
materials as grain or sand. To pump water from a river, for example, the
lower end is placed in the river and water rises up the spiral threads of the
screw as it is revolved.

14. Ptolemaic System
Ptolemy described an Earth-
centered solar system in his book
The Almagest. The system fit well with the
Medieval world view, as shown
by this illustration of Dante.

15. Hindu-Arabian Period (200 B.C. to 1250 A.D. )
A. Development and Spread of Hindu-Arabic Numbers
• A numeration system using base 10, positional notation, the zero symbol
and powerful arithmetic techniques is developed by the Hindus, approx.
150 B.C. to 800 A.D..
• The Hindu numeration system is adopted by the Arabs and spread
throughout their sphere of influence (approx. 700 A.D. to 1250 A.D.).
B. Preservation of Greek Mathematics
• Arab scholars copied and studied Greek mathematical works, principally
in Baghdad.
C. Development of Algebra and Trigonometry
• Arab mathematicians find methods of solution for quadratic, cubic and
higher degree polynomial equations. The English word “algebra” is
derived from the title of an Arabic book describing these methods.
• Hindu trigonometry, especially sine tables, is improved and advanced by
Arab mathematicians

16. Baghdad and the House of Wisdom
About the middle of the ninth
century Bait Al-Hikma, the "House of
Wisdom" was founded in Baghdad
which combined the functions of a
library, academy, and translation
bureau.
Baghdad attracted scholars from the
Islamic world and became a great
center of learning.
Painting of ancient Baghdad

17. The Great Mosque of Cordoba
The Great Mosque, Cordoba
During the Middle Ages
Cordoba was the greatest
center of learning in Europe,
second only to Baghdad in the
Islamic world.

18. Arabic Translation of Apollonius’ Conic Sections.

19. Arabic Translation of Ptolemy’s Almagest
Pages from a
13th
century
Arabic edition of
Ptolemy’s
Almagest.

20. Al-Khwarizmi
Abu Abdullah Muhammad bin Musa al-
Khwarizmi, c. 800 A.D. was a Persian
mathematician, scientist, and author.
He worked in Baghdad and wrote all his
works in Arabic.
He developed the concept of an
algorithm in mathematics. The words
"algorithm" and "algorism" derive
ultimately from his name. His
systematic and logical approach to
solving linear and quadratic equations
gave shape to the discipline of algebra,
a word that is derived from the name of
his book on the subject, Hisab al-jabr
wa al-muqabala (“al-jabr” became
“algebra”).
He was also instrumental in promoting
the Hindu-arabic numeration system.

21. Evolution of Hindu-Arabic Numerals

22. Leonardo of Pisa
From Leonardo of Pisa’s famous book Liber Abaci (1202 A.D.):
"These are the nine figures of the Indians: 9 8 7 6 5 4 3 2 1.
With these nine figures, and with this sign 0 which in Arabic is
called zephirum, any number can be written, as will be
demonstrated."

23. “Jealousy” Multiplication
Page from an anonymous Italian
treatise on arithmetic, 1478.
16th
century Arab copy of an early
work using Indian numerals to
show multiplication. Top example
is 3 x 64, bottom is 543 x 342.

24. Rediscovery of Greek Geometry
Luca Pacioli (1445 - 1514), a
Franciscan friar and
mathematician, stands at a
table filled with geometrical
tools (slate, chalk, compass,
dodecahedron model, etc.),
illustrating a theorem from
Euclid, while examining a
beautiful glass
rhombicuboctahedron half-
filled with water.

25. Pacioli and Leonardo Da Vinci
Luca Pacioli's 1509 book The Divine Proportion was illustrated by
Leonardo Da Vinci.
Shown here is a drawing of an icosidodecahedron and an "elevated"
form of it. For the elevated forms, each face is augmented with a
pyramid composed of equilateral triangles.

26. Early Modern Period (1450 A.D. – 1800 A.D.)
A. Trigonometry and Logarithms
• Publication of precise trigonometry tables, improvement of surveying
methods using trigonometry, and mathematical analysis of
trigonometric relationships. (approx. 1530 – 1600)
• Logarithms introduced by Napier in 1614 as a calculation aid. This
advances science in a manner similar to the introduction of the
computer.
B. Symbolic Algebra and Analytic Geometry
• Development of symbolic algebra, principally by the French
mathematicians Viete and Descartes
• The cartesian coordinate system and analytic geometry developed by
Rene Descartes and Pierre Fermat (1630 – 1640)
C. Creation of the Calculus
• Calculus co-invented by Isaac Newton and Gottfried Leibniz. Major
ideas of the calculus expanded and refined by others, especially the
Bernoulli family and Leonhard Euler. (approx. 1660 – 1750).
• A powerful tool to solve scientific and engineering problems, it opened
the door to a scientific and mathematical revolution.

27. Viète and Symbolic Algebra
In his influential treatise In Artem
Analyticam Isagoge (Introduction
to the Analytic Art, published
in1591) Viète demonstrated the
value of symbols. He suggested
using letters as symbols for
quantities, both known and
unknown.
François Viète
1540-1603

28. The Conic Sections and Analytic Geometry
General Quadratic Relation
Ax2
+ Bxy + Cy2
+ Dx + Ey + F = 0
Parabola
-x2
+ y = 0
Ellipse
4x2
+ y2
- 9 = 0
Hyperbola
x2
– y2
– 4 = 0

29. Some Famous Curves
Fermat’s Spiral
r2
= a2
θ
Archimede’s Spiral
r = aθ
Trisectrix of Maclaurin
y2
(a + x) = x2
(3a - x)
Lemniscate of Bernoulli
(x2
+ y2
)2
= a2
(x2
- y2
)
Limacon of Pascal
r = b + 2acos(θ)

30. Curves and Calculus: Common Problems
Find the area between curves.
Find the volume and surface
area of a solid formed by
rotating a curve.
Find the length of a curve.
Find measures of a curve’s shape.

31. Napier’s Logarithms
In his Mirifici Logarithmorum
Canonis descriptio (1614) the
Scottish nobleman John Napier
introduced the concept of
logarithms as an aid to
calculation.
John Napier
1550-1617

32. Kepler and the Platonic Solids
Johannes Kepler
1571-1630
Kepler’s first attempt to describe
planetary orbits used a model of
nested regular polyhedra
(Platonic solids).

33. Newton’s Principia – Kepler’s Laws “Proved”
Isaac Newton
1642 - 1727
Newton’s Principia Mathematica
(1687) presented, in the style of
Euclid’s Elements, a mathematical
theory for celestial motions due to the
force of gravity. The laws of Kepler
were “proved” in the sense that they
followed logically from a set of basic
postulates.

34. Newton’s Calculus
Newton developed the main
ideas of his calculus in private
as a young man. This research
was closely connected to his
studies in physics. Many years
later he published his results to
establish priority for himself as
inventor the calculus.
Newton’s Analysis Per
Quantitatum Series, Fluxiones,
Ac Differentias, 1711, describes
his calculus.

35. Leibniz’s Calculus
Leibniz and Newton independently
developed the calculus during the
same time period. Although Newton’s
version of the calculus led him to his
great discoveries, Leibniz’s concepts
and his style of notation form the
basis of modern calculus.
Gottfied Leibniz
1646 - 1716
A diagram from Leibniz's famous
1684 article in the journal Acta
eruditorum.

36. Leonhard Euler
Leonhard Euler was of the generation that followed
Newton and Leibniz. He made contributions to
almost every field of mathematics and was the
most prolific mathematics writer of all time.
His trilogy, Introductio in analysin infinitorum,
Institutiones calculi differentialis, and Institutiones
calculi integralis made the function a central part of
calculus. Through these works, Euler had a deep
influence on the teaching of mathematics. It has
been said that all calculus textbooks since 1748
are essentially copies of Euler or copies of copies
of Euler.
Euler’s writing standardized modern mathematics
notation with symbols such as:
f(x), e, π, i and ∑ .
Leonhard Euler
1707 - 1783

37. Modern Period (1800 A.D. – Present)
A. Non-Euclidean Geometry
• Gauss, Lobachevsky, Riemann and others develop alternatives to Euclidean geometry
in the 19th century.
• The new geometries inspire modern theories of higher dimensional spaces, gravitation,
space curvature and nuclear physics.
B. Set Theory
• Cantor studies infinite sets and defines transfinite numbers
• Set theory used as a theoretical foundation for all of mathematics
C. Statistics and Probability
• Theories of probability and statistics are developed to solve numerous practical
applications, such as weather prediction, polls, medical studies etc.; they are also used
as a basis for nuclear physics
D. Computers
• Development of electronic computer hardware and software solves many previously
unsolvable problems; opens new fields of mathematical research.
E. Mathematics as a World-Wide Language
• The Hindu-Arabic numeration system and a common set of mathematical symbols are
used and understood throughout the world.
• Mathematics expands into many branches and is created and shared world-wide at an
ever-expanding pace; it is now too large to be mastered by a single mathematician

38. Non-Euclidean Geometry
In the 19th
century Gauss, Lobachevsky, Riemann and other
mathematicians explored the possibility of alternative
geometries by modifying the 5th
postulate of Euclid’s Elements.
This opened the door to greater abstraction in geometrical
thinking and expanded the ways in which scientists use
mathematics to model physical space.
Bernhard Riemann
1826 - 1866
Nikolai Lobachevsky
1792 - 1856
Carl Gauss
1777 - 1855

39. Pioneers of Statistics
In the early 20th
century
a group of English
mathematicians and
scientists developed
statistical techniques
that formed the basis
of contemporary
statistics.
William Gosset
1876 - 1937
Francis Galton
1822 - 1911
Karl Pearson
1857 - 1936
Ronald Fisher
1890- 1962

40. Gossett’s Student t Curve
Diagram from the ground breaking 1908 article “Probable
Error of the Mean” by Student (William S. Gossett).

41. ENIAC: First Electronic Computer
In 1946 John W.
Mauchly and J.
Presper Eckert
Jr. built ENIAC at
the University of
Pennsylvania.
It weighed 30
tons, contained
18,000 vacuum
tubes and could
do 100,000
calculations per
second.

42. Von Neumann and the Theory of Computing
John von Neumann with Robert
Oppenheimer in front of the computer built
for the Institute of Advanced Studies in
Princeton, early 1950s.
Von Neumann
Architecture

43. Computer Generated Images
Equicontour Surface of a Random Function

44. Computer Generated Images
Evolution of a three dimensional cellular automata.