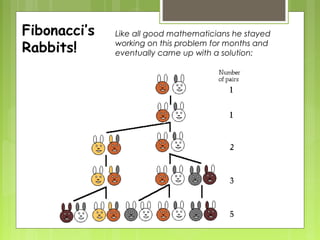
Fibonacci, originally named Leonardo de Pisa, was an Italian mathematician known for his famous rabbit problem which led to the creation of the Fibonacci sequence. This sequence, formed by adding the two previous numbers together, appears throughout nature, though not every plant exhibits Fibonacci numbers. The document also explores various natural patterns like symmetry, spirals, fractals, and tessellations, encouraging fifth graders to become 'pattern hunters' to observe and sketch these patterns.