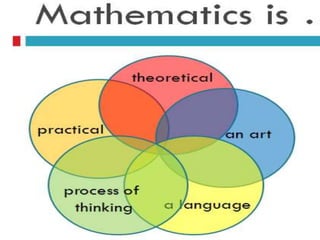
The document discusses several important mathematicians and their contributions throughout history: - Leonhard Euler made significant advances in areas like calculus, trigonometry, and number theory. He introduced modern mathematical notation that is still used today. - Carl Gauss was one of the greatest mathematicians, making influential discoveries in fields like algebra, geometry, statistics, and number theory. He laid the foundations of number theory, which computers rely on. - John von Neumann designed the architecture underlying modern computers. The basic steps that allow computers to function were conceived by him. - Benoit Mandelbrot discovered fractal geometry, which is fundamental to computer graphics and animation software. Fractals also have applications in technology like

2.  In 18th century mathematics is already a
modern science
 Mathematics begins to develop very fast
because of introducing it to schools
 Therefore everyone have a chance to learn
the basic learnings of mathematics

3.  Thanks to that, large number of new
mathematicians appear on stage
 There are many new ideas, solutions to old
mathematical problems,researches which
lead to creating new fields of mathematics.
 Old fields of mathematics are also
expanding.

6.  He was a Swiss mathematician.
 Johann Bernoulli made the biggest influence on
Leonhard.
 1727 he went to St Petersburg where he worked in
the mathematics department and became in 1731
the head of this department.
 1741 went in Berlin and worked in Berlin Academy
for 25 years and after that he returned in St
Ptersburg where he spent the rest of his life..

7.  Euler worked in almost all areas of mathematics: geometry,
calculus, trigonometry, algebra,applied mathematics,
graph theory and number theory, as well as , lunar theory,
optics and other areas of physics.
 Concept of a function as we use today was introduced by
him;he was the first mathematician to write f(x) to denote
function
 He also introduced the modern notation for the
trigonometric functions, the letter e for the base of the
natural logarithm (now also known as Euler’s number), the
Greek letter Σ for summations and the letter i to denote the
imaginary unit

9.  There aren't many subjects that Newton didn't have a
huge impact in — he was one of the inventors of
calculus, built the first reflecting telescope and helped
establish the field of classical mechanics with his
seminal work, "Philosophiæ Naturalis Principia
Mathematica."
 He was the first to decompose white light into its
component colors and gave us the three laws of
motion, now known as Newton's laws.

10.  We would live in a very different world had Sir Isaac
Newton not been born.
 Other scientists would probably have worked out most
of his ideas eventually, but there is no telling how long
it would have taken and how far behind we might have
fallen from our current technological trajectory.

12.  Isaac Newton is a hard act to follow, but if anyone can
pull it off, it's Carl Gauss.
 If Newton is considered the greatest scientist of all
time, Gauss could easily be called the greatest
mathematician ever.
 Carl Friedrich Gauss was born to a poor family in
Germany in 1777 and quickly showed himself to be a
brilliant mathematician.
 You can find his influence throughout algebra,
statistics, geometry, optics, astronomy and many other
subjects that underlie our modern world.

13.  He published "Arithmetical Investigations," a
foundational textbook that laid out the tenets of
number theory (the study of whole numbers).
 Without number theory, you could kiss computers
goodbye.
 Computers operate, on a the most basic level, using
just two digits — 1 and 0, and many of the
advancements that we've made in using computers to
solve problems are solved using number theory.

15.  John von Neumann was born in Budapest a few years
after the start of the 20th century, a well-timed birth
for all of us, for he went on to design the architecture
underlying nearly every single computer built on the
planet today.
 Von Neumann received his Ph.D in mathematics at
the age of 22 while also earning a degree in chemical
engineering to appease his father, who was keen on his
son having a good marketable skill.
 In 1930, he went to work at Princeton University with
Albert Einstein at the Institute of Advanced Study.

16.  Right now, whatever device or computer that you are
reading this on, be it phone or computer, is cycling
through a series of basic steps billions of times over each
second; steps that allow it to do things like render
Internet articles and play videos and music, steps that
were first thought up by John von Neumann.
 Before his death in 1957, von Neumann made important
discoveries in set theory, geometry, quantum mechanics,
game theory, statistics, computer science and was a vital
member of the Manhattan Project.

18.  Alan Turing a British mathematician who has been call the
father of computer science.
 During World War II, Turing bent his brain to the problem
of breaking Nazi crypto-code and was the one to finally
unravel messages protected by the infamous Enigma
machine.
 Alan Turing's career and life ended tragically when he was
arrested and prosecuted for being gay.
 He was found guilty and sentenced to undergo hormone
treatment to reduce his libido, losing his security clearance
as well. On June, 8, 1954, Alan Turing was found dead of
apparent suicide by his cleaning lady.


19.  Alan Turing was instrumental in the development of
the modern day computer.
 His design for a so-called "Turing machine" remains
central to how computers operate today.
 The "Turing test" is an exercise in artificial intelligence
that tests how well an AI program operates; a program
passes the
 Turing test if it can have a text chat conversation with
a human and fool that person into thinking that it too
is a person.

21.  Mandelbrot was born in Poland in 1924 and had to flee
to France with his family in 1936 to avoid Nazi
persecution.
 After studying in Paris, he moved to the U.S. where he
found a home as an IBM Fellow.
 Working at IBM meant that he had access to cutting-
edge technology, which allowed him to apply the
number-crunching abilities of electrical computer to
his projects and problems.
 Benoit Mandelbrot died of pancreatic cancer in 2010.

22.  Benoit Mandelbrot landed on this list thanks to his
discovery of fractal geometry.
 Fractals, often-fantastical and complex shapes built on
simple, self-replicable formulas, are fundamental to
computer graphics and animation.
 Without fractals, it's safe to say that we would be
decades behind where we are now in the field of
computer-generated images.
 Fractal formulas are also used to design cellphone
antennas and computer chips, which takes advantage of
the fractal's natural ability to minimize wasted space.

23. •The modern world would not exist without
maths
•With maths you can tell the future and save
lives
•Maths lies at the heart of art and music
•Maths is a subject full of mystery, surprise
and magic

25. Linear algebra, graph theory, SVDGoogle:
Error correcting codes: Galois theory
Internet: Network theory
Security: Fermat, RSA
Mathematicians really have made the modern world possible
Medical imaging: Radon Transform
Communications: FFT, Shannon
Medical Statistics: Nightingale