This document provides a summary of key trigonometric formulas and identities. It includes 16 sections that cover topics such as the definitions of trigonometric functions, special right triangle ratios, sine and cosine laws, trigonometric function relationships, addition and subtraction formulas, double and half angle formulas, and the periodicity and graphs of the six trigonometric functions.

1. Maths 3/4: Trigonometry
Formulas & Identities
1.Trigonometric Functions of Acute Angles
sin X = a / c
csc X = c / a Basic
tan X = a / b
cot X = b / a
cos X = b / c
sec X = c / b
1.Special Triangles
Special triangles may be used to find trigonometric
functions of special angles: 30, 45 and 60 degress.

2. 2.Sine and Cosine Laws in Triangles
1 - The sine law
sin A / a = sin B / b = sin C / c
2 - The cosine laws
a 2 = b 2 + c 2 - 2 b c cos A
b 2 = a 2 + c 2 - 2 a c cos B
c 2 = a 2 + b 2 - 2 a b cos C
3.Relations Between Trigonometric Functions
cscX = 1 / sinX, sinX = 1 / cscX
secX = 1 / cosX, cosX = 1 / secX
tanX = 1 / cotX, cotX = 1 / tanX
tanX = sinX / cosX, cotX = cosX / sinX
4.Pythagorean Identities
sin 2X + cos 2X = 1
1 + tan 2X = sec 2X
1 + cot 2X = csc 2X
5.Negative Angle Identities

3. sin(-X) = - sinX , odd function
csc(-X) = - cscX , odd function
cos(-X) = cosX , even function
sec(-X) = secX , even function
tan(-X) = - tanX , odd function
cot(-X) = - cotX , odd function
6.Cofunctions Identities
sin(pi/2 - X) = cosX
cos(pi/2 - X) = sinX
tan(pi/2 - X) = cotX
cot(pi/2 - X) = tanX
sec(pi/2 - X) = cscX
csc(pi/2 - X) = secX
7.Addition Formulas
cos(X + Y) = cosX cosY - sinX sinY
cos(X - Y) = cosX cosY + sinX sinY
sin(X + Y) = sinX cosY + cosX sinY
sin(X - Y) = sinX cosY - cosX sinY
tan(X + Y) = [ tanX + tanY ] / [ 1 - tanX tanY]
tan(X - Y) = [ tanX - tanY ] / [ 1 + tanX tanY]
cot(X + Y) = [ cotX cotY - 1 ] / [ cotX + cotY]
cot(X - Y) = [ cotX cotY + 1 ] / [ cotX - cotY]
8.Sum to Product Formulas
cosX + cosY = 2cos[ (X + Y) / 2 ] cos[ (X - Y) / 2 ]
sinX + sinY = 2sin[ (X + Y) / 2 ] cos[ (X - Y) / 2 ]

4. 9.Difference to Product Formulas
cosX - cosY = - 2sin[ (X + Y) / 2 ] sin[ (X - Y) / 2 ]
sinX - sinY = 2cos[ (X + Y) / 2 ] sin[ (X - Y) / 2 ]
10.Product to Sum/Difference Formulas
cosX cosY = (1/2) [ cos (X - Y) + cos (X + Y) ]
sinX cosY = (1/2) [ sin (X + Y) + sin (X - Y) ]
cosX sinY = (1/2) [ sin (X + Y) - sin[ (X - Y) ]
sinX sinY = (1/2) [ cos (X - Y) - cos (X + Y) ]
11.Difference of Squares Formulas
sin 2X - sin 2Y = sin(X + Y)sin(X - Y)
cos 2X - cos 2Y = - sin(X + Y)sin(X - Y)
cos 2X - sin 2Y = cos(X + Y)cos(X - Y)
12.Double Angle Formulas
sin(2X) = 2 sinX cosX
cos(2X) = 1 - 2sin 2X = 2cos 2X - 1
tan(2X) = 2tanX / [ 1 - tan 2X ]
13.Multiple Angle Formulas
sin(3X) = 3sinX - 4sin 3X
cos(3X) = 4cos 3X - 3cosX
sin(4X) = 4sinXcosX - 8sin 3XcosX
cos(4X) = 8cos 4X - 8cos 2X + 1
14.Half Angle Formulas

5. sin (X/2) = + or - SQRT [ (1 - cosX) / 2 ]
cos (X/2) = + or - SQRT [ (1 + cosX) / 2 ]
tan (X/2) = + or - SQRT [ (1 - cosX) / (1 - cosX) ]
= sinX / (1 + cosX) = (1 - cosX) / sinX
15.Power Reducing Formulas
sin 2X = 1/2 - (1/2)cos(2X))
cos 2X = 1/2 + (1/2)cos(2X))
sin 3X = (3/4)sinX - (1/4)sin(3X)
cos 3X = (3/4)cosX + (1/4)cos(3X)
sin 4X = (3/8) - (1/2)cos(2X) + (1/8)cos(4X)
cos 4X = (3/8) + (1/2)cos(2X) + (1/8)cos(4X)
sin 5X = (5/8)sinX - (5/16)sin(3X) + (1/16)sin(5X)
cos 5X = (5/8)cosX + (5/16)cos(3X) + (1/16)cos(5X)
sin 6X = 5/16 - (15/32)cos(2X) + (6/32)cos(4X) -
(1/32)cos(6X)
cos 6X = 5/16 + (15/32)cos(2X) + (6/32)cos(4X) +
(1/32)cos(6X)
16.Trigonometric Functions Periodicity
sin (X + 2Pi) = sin X , period 2Pi
cos (X + 2Pi) = cos X , period 2Pi
sec (X + 2Pi) = sec X , period 2Pi
csc (X + 2Pi) = csc X , period 2Pi
tan (X + Pi) = tan X , period Pi
cot (X + Pi) = cot X , period Pi
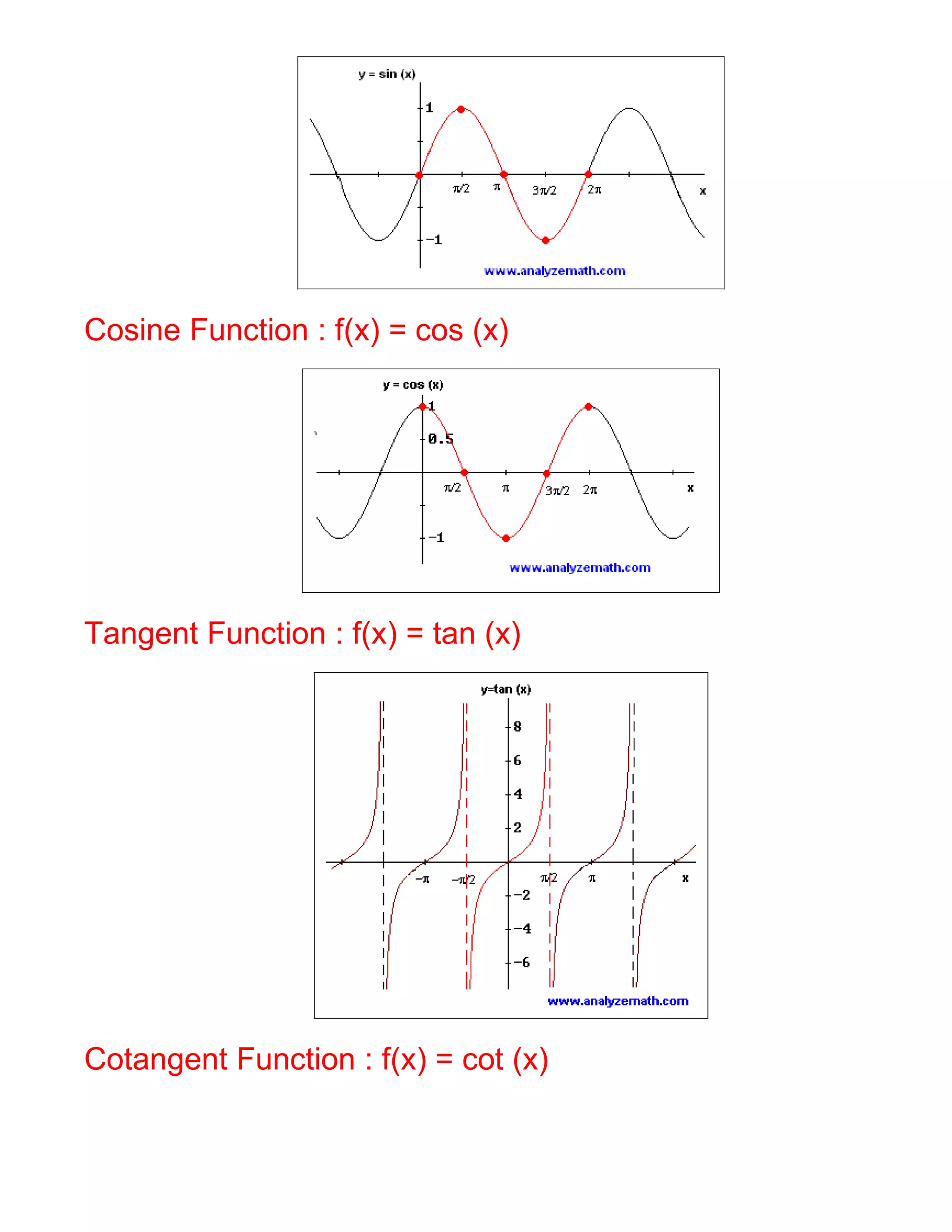
18. Graphs of The Six Trigonometric Functions.
Sine Function : f(x) = sin (x)

6. Cosine Function : f(x) = cos (x)
Tangent Function : f(x) = tan (x)
Cotangent Function : f(x) = cot (x)

7. Secant Function : f(x) = sec (x)
Cosecant Function : f(x) = csc (x)