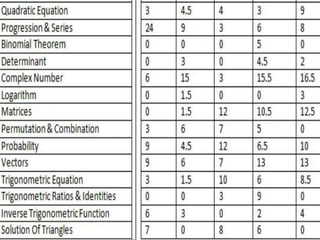
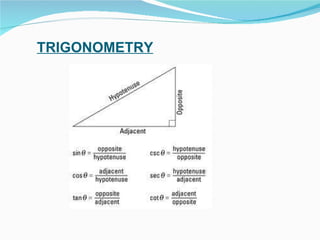
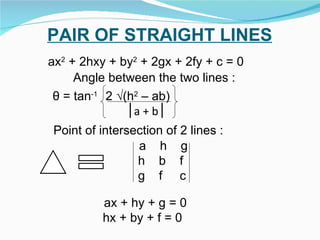
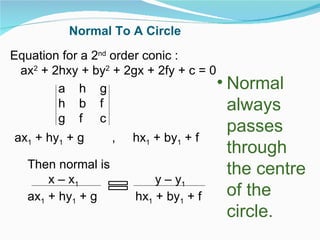
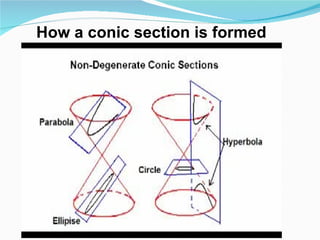
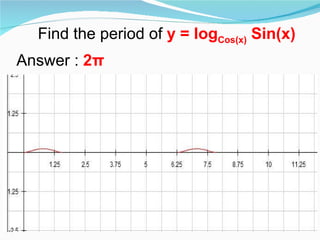
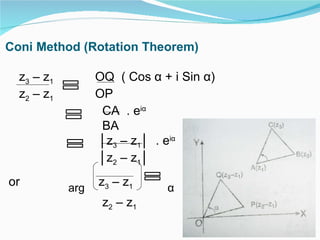
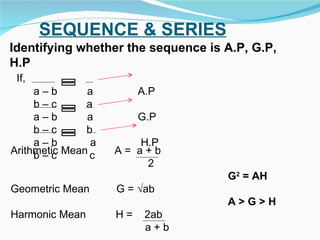
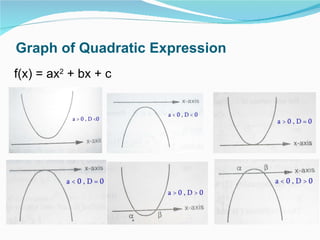
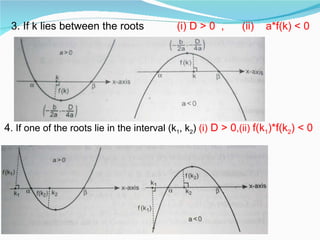
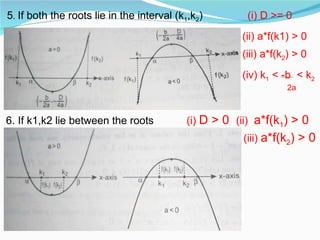
This document provides an overview of key topics in mathematics including trigonometry, coordinate geometry, calculus, algebra, sequences and series, and permutations and combinations. It discusses important formulas and concepts for each topic, as well as strategies for understanding and solving problems. Key areas covered include trigonometric functions and their inverses, equations of circles, parabolas, ellipses and hyperbolas, limits, derivatives, integrals, complex numbers, and series.

1. MATHEMATICS FUNDAE

2. A game of numbers. It is also a tool used in day to day life. Needed in Physics and Chemistry also. Helps in getting a good rank. What is Maths?

3. HOW TO ENJOY MATHEMATICS Focus On Basics . Try To Understand The Formulae. Predict Its Application. Match With The Applications As In Books. Think WHY? Write The Concepts Which You Are Going To Use On The Paper Before Starting The Solution Of Problem.

4. Important Chapters??

6. TRIGONOMETRY

7. Trigonometric Functions and Equations Widely used in other chapters of mathematics. Requires lot of practice. It has only formulae. Try to see some pattern in the formulae and then learned.

8. Inverse Trigonometric Functions Very conceptual Requires the use of graphs Should be studied after studying functions.

9. Topics are interlinked Visualization of problems Follow ‘read & draw strategy’ Some formulae should be learned CO – ORDINATE GEOMETRY

10. STRAIGHT LINE Normal Form : x cos α + y sin α = p Parametric Form : x – x 1 x – x 2 r cos θ sin θ

11. Equation of angle bisectors a 1 x + b 1 y +c 1 a 2 x + b 2 y + c 2 √ a 1 2 + b 1 2 √a 2 2 + b 2 2 If c 1 , c 2 > 0, then bisector containing origin is given by +ve sign ACUTE & OBTUSE ANGLE BISECTOR

12. Use of Reflection

14. ax 2 + 2hxy + by 2 + 2gx + 2fy + c = 0 Angle between the two lines : θ = tan -1 2 √(h 2 – ab) │ a + b│ Point of intersection of 2 lines : a h g h b f g f c ax + hy + g = 0 hx + by + f = 0 PAIR OF STRAIGHT LINES

15. CIRCLE (x – a) 2 + (y – b) 2 = r 2 Equation of the tangent : Point Form Parametric Form Slope Form Replace x 2 xx 1 y 2 yy 1 2x (x + x 1 ) 2y (y + y 1 ) 2xy (xy 1 + x 1 y) Only valid for a two degree equation

16. Normal To A Circle Equation for a 2 nd order conic : ax 2 + 2hxy + by 2 + 2gx + 2fy + c = 0 Normal always passes through the centre of the circle. Then normal is x – x 1 y – y 1 ax 1 + hy 1 + g hx 1 + by 1 + f a h g h b f g f c ax 1 + hy 1 + g , hx 1 + by 1 + f

17. Radical Axis S – S’ = 0 Perpendicular to the line joining the centres. Bisects the direct common tangents. For 3 circles, taking 2 at a time, they are concurrent.

18. The curve y = x 3 – 3x + 2 and x + 3y = 2 intersect in points (x 1 ,y 1 ), (x 2 ,y 2 ) and (x 3 ,y 3 ). Then the point P(A,B) where A = Σ x i and B = Σ y i lies on the line (A) x – 3y = 5 (B) x + y = 1 (C) 3x – 7 = y (D) 2x + y = 2

19. Conic Section ax 2 + 2hxy + by 2 + 2gx + 2fy + c = 0

20. How a conic section is formed

21. PARABOLA Focal Chord t 1 t 2 = -1 Length (PQ) = a*(t 2 – t 1 ) 2 Tangents at P & Q will be perpendicular to each other Length of Latus Rectum : 4 * PS * QS PS + QS

22. Tangents Slope Form : Point of intersection of tangents: ( at 1 t 2 , a(t 1 + t 2 ) ) y = mx + a m Remembering Method : G O A (GOA rule) GM of at 1 2 & at 2 2 , AM of 2at 1 & 2at 2 i.e. at 1 t 2 i.e. a(t 1 + t 2 )

23. Equation of tangent to parabolas of different form :

24. Co – Normal Points Properties : m 1 + m 2 + m 3 = 0 y 1 + y 2 + y 3 = 0 For the normals to be real h > 2a For the normals to be real and distinct 27ak 2 < 4(h-2a) 3

25. ELLIPSE Tangent in slope form : y = mx + √ (a 2 m 2 + b 2 ) - Normal in slope form : y = mx - m (a 2 – b 2 ) + √ (a 2 + b 2 m 2 )

26. Co – Normal Points 4 Normals can be drawn from any point to an ellipse. α + β + λ + δ = (2n + 1) π Properties:

27. Sin ( α + β ) + Sin ( β + λ ) + Sin ( λ + α ) = 0 Co – Normal Points lie on a fixed curve called Apollonian Rectangular Hyperbola A.R.H (a2 – b2)xy + b2kx – a2hy = 0

28. Director Circle : Locus of the points from which perpendicular tangents can be drawn x 2 + y 2 = a 2 + b 2

29. Reflection Property : Ray passing through a focus, passes through the other focus after reflection.

30. HYPERBOLA Asymptotes Tangent to the hyperbola at infinity Properties : Difference between hyperbola and pair of asymptotes is constant. Hyperbola and its conjugate hyperbola have the same asymptotes. x 2 - y 2 = 0 a 2 b 2

31. Angle between two asymptotes is 2tan -1 (b/a) Asymptotes pass through the centre of the hyperbola. Co – Ordinate axes are angular bisector of the two asymptotes. Hyperbola, Asymptotes and Conjugate Hyperbola are in A.P i.e. C + H = 2A

32. If normal at P (2, 1.5√3) meets the major axis of the ellipse x 2 + y 2 = 1 at Q. S and S’ are 16 9 foci of given ellipse, then SQ:S’Q is (A) 8 – √7 8 + √7 (B) 4 + √7 4 – √7 (C) 8 + √7 8 – √7 4 – √7 4 + √7

33. DIFFERENTIAL CALCULUS

34. FUNCTIONS Most Important Is Concept Of DOMAIN And RANGE . Knowledge About Some Important Functions Like LOGARATHMIC, TRIGONOMETRIC, GREATEST INTEGER etc. Focus On Domain And Range Of These Functions.

35. Give Attention To COMPOSITE FUNCTIONS . For Finding PERIOD, Be Careful About CONSTANT FUNCTION. HOW TO SOLVE PROBLEMS IN EXAMS ? Identify The Nature Of Function . Coordinate With Its Domain And Range.

36. Think Practically. Go What The Question Says……. Get The Knowledge Of Symmetry About Any Point Or Line.

37. Find the period of y = log Cos(x) Sin(x) Answer : 2 π

38. LIMIT Condition For EXISTANCE OF LIMIT Remember Some Important Expansions. L’HOSPITAL RULE Try To Simplify The Question If You Get A Hard And Tough Looking Problem. 95% Of Such Problems Becomes Easy After Simplification

39. In Case When x Tends To Infinity In Algebraic /Algebraic Function Be Careful About Constants If Given In Question.

40. CONTINUITY AND DIFFERENTIABILITY Concept Of LIMIT Should Be Clear Before Attempting The Questions Of Continuity. Remember The Approach Of Continuity At End Points . For Differentiability Of Function, Careful Where To Use Basic Funda And Where Direct Differntiation .

41. Differentiability At End Points In A Closed Or Open Interval. Differentiability Implies Contuinity .

42. APPLICATIONS OF dy/dx ROLLE’S THEOREM . LAGRANGE’S MEAN VALUE THEOREM. Use Of dy/dx In Deciding The Nature Of Curve. Try To Co-Relate Max. And Min. With The Help Of Graph.

43. Use nth Derivative Test. Concentrate On Maxima And Minima Of Discontinuous Function.

44. INTEGRAL CALULUS

45. INDEFINITE INTEGRAL Get Some Important Results. Use By Parts Method Whenever There Is Any Scope. Rearrangement Is Your Motto . Get The Approach Of Some Important Forms.

46. DEFINITE INTEGRALS An Easy Version Of Indefinite Integrals. Use Of Properties Are Very Useful. No Need Of Gamma Function , Walli’s Function etc. Maximum And Minimum Value of Integral Are Very Helpful During Exams.

47. Newton Method Of Differentiation Of Integrals. For Area , First Draw The Curve. Find Symmetrical Parts. Be Careful About Sign Of Integration.

48. (A) f(2012) + f(-2012) (B) f(2012) – f(-2012) (C) 0 (D) 2012

49. DIFFERENTIAL EQUATION Order And Degree. Degree Is Defined For Polynomial Equation Only. First Step Is To Check If Equation Can Be Solved By Rearranging. If Equation Is Of Form f(ax+by+c) , Then Solve It By Taking ax+by+c=t.

50. For Homogeneous Equation , Use y=vx. Concept Of Exact Equations. Linear Equation And Conversion Into Linear Equations.

51. ALGEBRA

52. COMPLEX NUMBER De Moivre’s Theorem (Cos θ + i Sin θ ) n = Cos n θ + i Sin n θ If z = (Cos θ 1 + i Sin θ 1 ) (Cos θ 2 + i Sin θ 2 ) (Cos θ 3 + i Sin θ 3 )……………..(Cos θ n + I Sin θ n ) then z = Cos ( θ 1 + θ 2 + θ 3 +………+ θ n) + i Sin ( θ 1 + θ 2 + θ 3 +………+ θ n ) If z = r(Cos θ + i Sin θ ) and n is a positive integer, then then z 1/n = r 1/n Cos (2k π + θ ) + i Sin (2k π + θ ) n n where k = 0,1,2,3………,(n-1)

53. Coni Method (Rotation Theorem) z 3 – z 1 OQ ( Cos α + i Sin α ) z 2 – z 1 OP CA . e i α BA │ z 3 – z 1 │ . e i α │ z 2 – z 1 │ or arg z 3 – z 1 α z 2 – z 1

54. Co – Ordinate in terms of Complex Equation of Straight Line : z – z 1 = z – z 1 z 2 – z 1 z 2 – z 1 Circle : zz + az + az + b = 0 , Centre is ‘-a’ radius = √aa - b

55. SEQUENCE & SERIES Identifying whether the sequence is A.P, G.P, H.P If, a – b a A.P b – c a a – b a G.P b – c b a – b a H.P b – c c Arithmetic Mean A = a + b 2 G 2 = AH Geometric Mean G = √ab A > G > H Harmonic Mean H = 2ab a + b

56. Some tips : If first common difference is in A.P take the General Term as ‘ax 2 + bx +c’ and determine a, b, c by solving for known values. S n = 1 + 2 + 4 + 7 + 11 + ……. T n = an 2 + bn + c , a = 0.5 , b = -0.5 , c = 1 S n = Σ T n

57. If second common difference is in A.P then take the cubic expression as the General Term and solve for constants.

58. Solution : S n = cn 2 T n = S n – S n-1 = cn 2 – c(n-1) 2 = c(2n – 1) T n 2 = c 2 (2n – 1) 2 S n = Σ T n * Shortcut Method : Put n = 1 in the question If the sum of first n terms of an A.P is cn 2 , then the sum of squares of these n terms is (A) n (4n 2 – 1)c 2 6 (B) n(4n 2 + 1)c 2 3 n(4n 2 – 1)c 2 3 n(4n 2 + 1)c 2 6

59. QUADRATIC EQUATION ax 2 + bx +c = 0 Conditions For A Common Root : ax 2 + bx + c = 0 , a’x 2 + b’x +c’ = 0 a = b = c a’ b’ c’ Note : To find the common root between the two equations, make the same coefficient of x 2 in both the equations and then subtract the 2 equations.

60. Graph of Quadratic Expression f(x) = ax 2 + bx + c

61. Location Of Roots 1. If both the roots are less than k (i) D >= 0 , (ii) a*f(k) > 0 , (iii) k > -b 2a 2 . If both the roots are greater than k (i) D >= 0 , (ii) a*f(k) > 0 , (iii) k < -b 2a

62. 3. If k lies between the roots (i) D > 0 , (ii) a*f(k) < 0 4 . If one of the roots lie in the interval (k 1 , k 2 ) (i) D > 0 ,(ii) f(k 1 )*f(k 2 ) < 0

63. 5 . If both the roots lie in the interval (k 1 ,k 2 ) (i) D >= 0 6. If k1,k2 lie between the roots (i) D > 0 (ii) a*f(k 1 ) > 0 (iii) a*f(k 2 ) > 0 (iv) k 1 < -b < k 2 2a (iii) a*f(k 2 ) > 0 (ii) a*f(k1) > 0

64. PERMUTATION & COMBINATION 1. Permutation of n different things taking r at a time = n P r 2. Permutation of n things taken all at a time, p are alike of one kind, q are alike of 2 nd kind, r are alike of 3 rd kind, rest are different n! p! q! r! 3. Number of permutations of n different things taken r at a time, when each thing may be repeated any no. of times n r Circular Permutation When anticlockwise and clockwise are treated as different : (n – 1)! When anticlockwise and clockwise are treated as same : (n – 1)! 2

65. COMBINATION 1. Combination of n different things taking r at a time : n C r 2 . Combination of n different things taking r at a time, when k particular objects occur is: n-k C r-k When k particular objects never occur : n-k C r 3. Combination of n different things selecting at least one of them : n C 1 + n C 2 + n C 3 + …………. + n C n = 2 n – 1 4. If out of (p+q+r+t) things, p are alike of one kind , q are alike of 2 nd kind, r are alike of 3 rd kind, and t are different, then the total number of combinations is : (p+1)(q+1)(r+1)*2 t – 1 5. Number of ways in which n different things can be arranged into r different groups is : n+r-1 P n

66. PROBABILITY Different types of events like Mixed Event, Independent Events, Complimentary Events. Learn some formulas like P(A U B) = P(A) + P(B) – P( A ∩ B) Conditional Probability. Baye’s Theorem or Inverse Probability. Binomial Theorem. Multinomial Theorem.

67. VECTORS AND 3D GEOMETRY

68. VECTORS You Must Give More Concentration On Vectors As It Is Also Required In Physics. You All Are Aware Of Simple Applications. Linearly Dependent And Linearly Independent Vectors.

69. Combination Of DOT And CROSS In Problems. For Solving Vector Equation, Just Try To Simplify It And Use The Conditions Given. If Sol. Requires r In Form Of Two Vectors a & b, Take r = λ a + µ b + σ (a×b)

70. In Case Of Three Non-Coplanar Vectors a, b And c, r = λ a + µb + σ c And Then Use/Apply The Conditions Given.

71. 3D-GEOMETRY Projection Of Segment Joining Two Points On Line. Angle Between Two Lines. Different Forms Of Straight Line Including Vector Form. Perpendicular Distance Of A Point From Line. Be Careful From Skew Lines .

72. Shortest Distance Between Two Skew Lines(Its Better To Use Detailed Approach). Equation Of Plane In Different Forms. Angle Between Line And Plane.Angle Between Two Planes. Just Try To Visualize Problem And Use Examination Hall To Put The Conditions In That Frame.

73. Derive The Following Yourself: Equation Of Plane Containing The Given Lines. Shortest Distance Between Two Lines In All Three Forms. Condition For Lines To Intersect.

74. TIPS SECTION

75. TIPS FOR EXAMINATION First Of All , Keep Faith In Yourself. On Entering Examination Hall, Your Confidence Level Is Like That You Are JEE-2012 Topper But Don’t Let This Confidence To Become Over-Confidence. During Examination, First Make A Quick View On Q. Paper.

76. Then Select The Question Which You Think ,You Will Solve Easily. Don’t Lose Your Confidence When You Are Not Able To Solve Any Problem. Keep In Mind, Some Questions Of JEE Are Not Given For Solving But Are Given To Leave . You Must Develop A Sense About Selection Of Question.

77. CONTACTS PHONE NO : 07501541135 EMAIL – ID : [email_address] Facebook.com/bilalshakir1 THANK YOU PHONE NO : 08927482599 EMAIL – ID : [email_address] Facebook.com : Ashnil Kumar