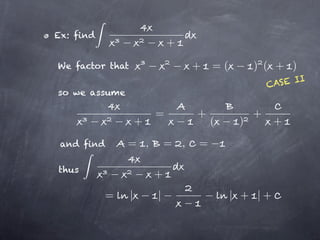Rational functions can be decomposed into the sum of partial fractions. This involves three main steps: 1. Use long division to decompose any improper rational functions into a polynomial plus a proper rational function. 2. Factor the denominator of the proper rational function into linear and irreducible quadratic factors. 3. Decompose the proper rational function into a sum of partial fractions with undetermined coefficients that are solved for. There are four cases to consider depending on whether the factors of the denominator are distinct, repeated, distinct quadratics, or repeated quadratics.

1. 7.4 Integration of
Rational Functions
Rational function: ratio of polynomials.
Ex: + +
+

2. 7.4 Integration of
Rational Functions
Rational function: ratio of polynomials.
Ex: + +
+
Fact: A rational function can always be
decomposed to summation of terms like
+
polynomials or ( + ) or ( + + ) where
A, B, etc. are constants.
Ex: − + +
= + + + −
− − + − ( − ) +
Partial Fractions

3. First step: if the rational function is
improper (the degree of numerator is more
than or equal to the degree of dominator),
use long division to decompose it to a
polynomial plus a proper rational function.
+
Ex: = + + +

4. First step: if the rational function is
improper (the degree of numerator is more
than or equal to the degree of dominator),
use long division to decompose it to a
polynomial plus a proper rational function.
+
Ex: = + + +
As a result:
+
= + + + | |+

5. Second step: factor the dominator of the
proper rational function to be a product of
linear factors and/or irreducible quadratic
factors.
+ + is irreducible if < .
Ex: + = ( + )
+ = ( )( + )
+ + =( ) ( + )

6. Third step: decompose the proper rational
function to be a sum of partial fractions by
method of undetermined coefficients.
+
Ex:
+

7. Third step: decompose the proper rational
function to be a sum of partial fractions by
method of undetermined coefficients.
+
Ex:
+
We factor + = ( )( + )

8. Third step: decompose the proper rational
function to be a sum of partial fractions by
method of undetermined coefficients.
+
Ex:
+
We factor + = ( )( + )
+
so assume = + +
+ +

9. Third step: decompose the proper rational
function to be a sum of partial fractions by
method of undetermined coefficients.
+
Ex:
+
We factor + = ( )( + )
+
so assume = + +
+ +
( + + ) +( + )
=
+

10. Third step: decompose the proper rational
function to be a sum of partial fractions by
method of undetermined coefficients.
+
Ex:
+
We factor + = ( )( + )
+
so assume = + +
+ +
( + + ) +( + )
=
+
thus = , = , =

11. CASE I: the dominator is a product of
distinct linear factors.
CASE II: the dominator is a product of
linear factors, some of which are repeated.
CASE III: the dominator contains distinct
irreducible quadratic factors.
Case IV: the dominator contains repeated
irreducible quadratic factors.

12. +
Ex: find
+

13. +
Ex: find
+
We already knew that
+
= +
+ ( ) ( + )
C AS E I

14. +
Ex: find
+
We already knew that
+
= +
+ ( ) ( + )
+ C AS E I
so
+
= | |+ | | | + |+

15. Ex: find
+

16. Ex: find
+
We factor that + =( ) ( + )
CAS E II

17. Ex: find
+
We factor that + =( ) ( + )
CAS E II
so we assume
= + +
+ ( ) +

18. Ex: find
+
We factor that + =( ) ( + )
CAS E II
so we assume
= + +
+ ( ) +
and find = , = , =

19. Ex: find
+
We factor that + =( ) ( + )
CAS E II
so we assume
= + +
+ ( ) +
and find = , = , =
thus
+
= | | | + |+