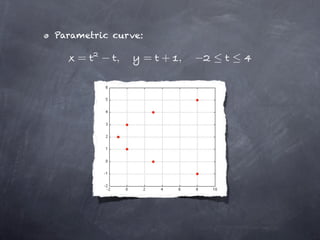
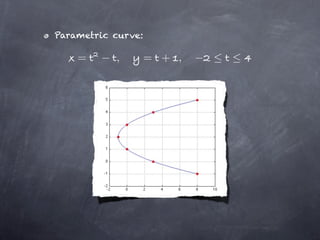
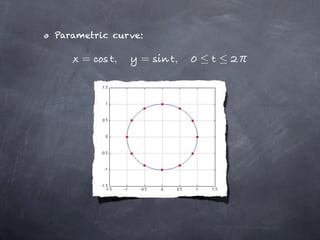
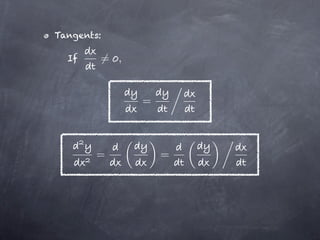
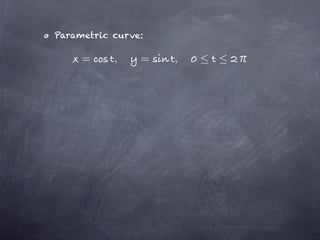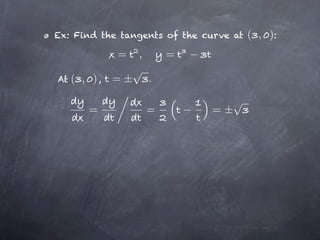The document discusses parametric equations and parametric curves. Parametric equations define curves using two equations, where x and y are defined in terms of a parameter t. Common examples of parametric curves are given. Parametric equations can be used to define circles by giving the x and y coordinates in terms of the center point and radius. The parameter t can be eliminated to obtain the Cartesian equation of the curve. Calculus can be applied to parametric curves to find tangents, areas, arc length, and surfaces of revolution. Formulas are given for finding the equations of tangent lines to parametric curves at a given value of t.

1. 10.1 Parametric Equations
Curves can be defined by functions:
= ( )
=
+
···
But they cannot describe all general curves.

2. Parametric equations:
= ( ), = ()
Ex:
= , = + ,
= , = ,
···

3. Parametric curve:
= , = + ,

4. Parametric curve:
= , = + ,

5. Parametric curve:
= , = + ,

6. Parametric curve:
= , = + ,

7. Parametric curve:
= , = ,

8. Parametric curve:
= , = ,

9. Parametric curve:
= , = ,

10. Parametric curve:
= , = ,

11. More examples:
= + , = + ,

12. More examples:
= = ,
+ +

13. More examples:
= + , = + ,

14. More examples:
=
=

15. Find parametric equations for the circles
with center ( , ) and radius .
y
r
(h,k)
o x

16. Find parametric equations for the circles
with center ( , ) and radius .
y
r
(h,k)
o x
= +
= +

17. Eliminate the parameter to find the Cartesian
equation of the curve.
= , = ,

18. Eliminate the parameter to find the Cartesian
equation of the curve.
= , = ,
+( ) =
y
(0,3)
o x

19. Eliminate the parameter to find the Cartesian
equation of the curve.
= , = ,
+( ) =
y s pos sible!
N ot alway
(0,3)
o x

20. 10.2 Calculus with
parametric Curves
= ( ), = ()
Tangents
Areas
Arc Length
Area of Surfaces of Revolution

21. Tangents:

22. Tangents:
If = ,
=

23. Tangents:
If = ,
=
= =

24. Tangents:
If = ,
=
= =
!!
=

25. Ex: Find the tangents of the curve at ( , ):
= , =

26. Ex: Find the tangents of the curve at ( , ):
= , =
At ( , ), = ± .
= = =±

27. Ex: Find the tangents of the curve at ( , ):
= , =
At ( , ), = ± .
= = =±
The equations of the tangents are:
=± ( )