The document discusses representations of lines, planes, and space curves in vector calculus. It defines the vector equation of a line, parametric equation of a line, and symmetric equation of a line. It also defines the vector equation and scalar equation of a plane. It then discusses representing space curves using parametric vector functions and calculating derivatives and integrals of vector functions, including rules for differentiation. It provides an example problem proving that the tangent line to a circle at a point is perpendicular to the line connecting that point to the circle's center.
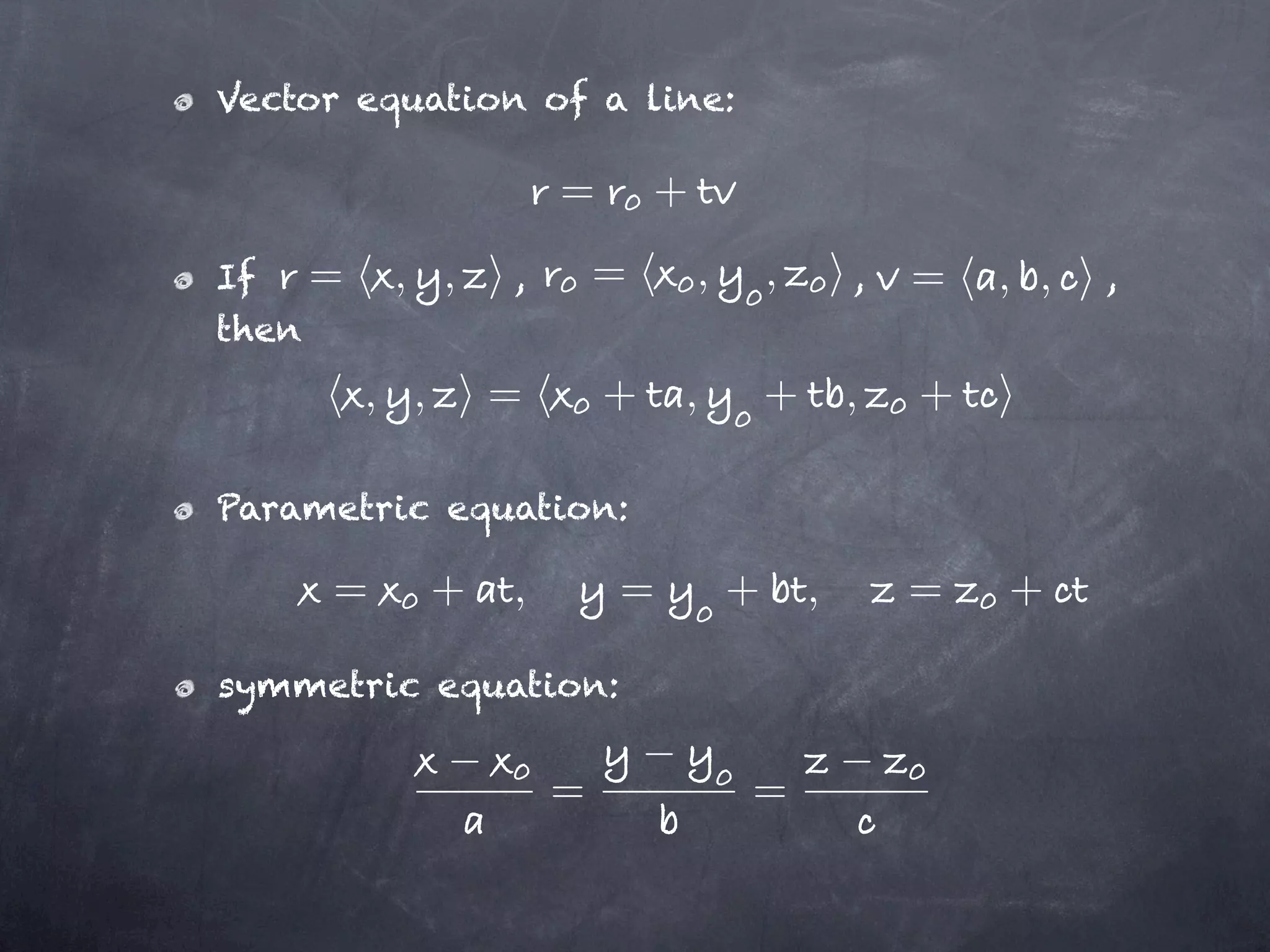












![Ex: Prove that the tangent line of a circle at
a point is perpendicular to the connecting
line of the point and the center.
A circle can be represented as | ( )| =
We want to show that () ()
( ) · ( ) = | ( )| =
[ ( ) · ( )] =](https://image.slidesharecdn.com/math12722011-12-05-111205162445-phpapp01/75/Calculus-II-35-14-2048.jpg)
![Ex: Prove that the tangent line of a circle at
a point is perpendicular to the connecting
line of the point and the center.
A circle can be represented as | ( )| =
We want to show that () ()
( ) · ( ) = | ( )| =
[ ( ) · ( )] =
( )· ( )=](https://image.slidesharecdn.com/math12722011-12-05-111205162445-phpapp01/75/Calculus-II-35-15-2048.jpg)
![Ex: Prove that the tangent line of a circle at
a point is perpendicular to the connecting
line of the point and the center.
A circle can be represented as | ( )| =
We want to show that () ()
( ) · ( ) = | ( )| =
[ ( ) · ( )] =
( )· ( )=
() ()](https://image.slidesharecdn.com/math12722011-12-05-111205162445-phpapp01/75/Calculus-II-35-16-2048.jpg)
